初中数学沪科版八年级下册19.2 平行四边形教课ppt课件

这是一份初中数学沪科版八年级下册19.2 平行四边形教课ppt课件，共36页。

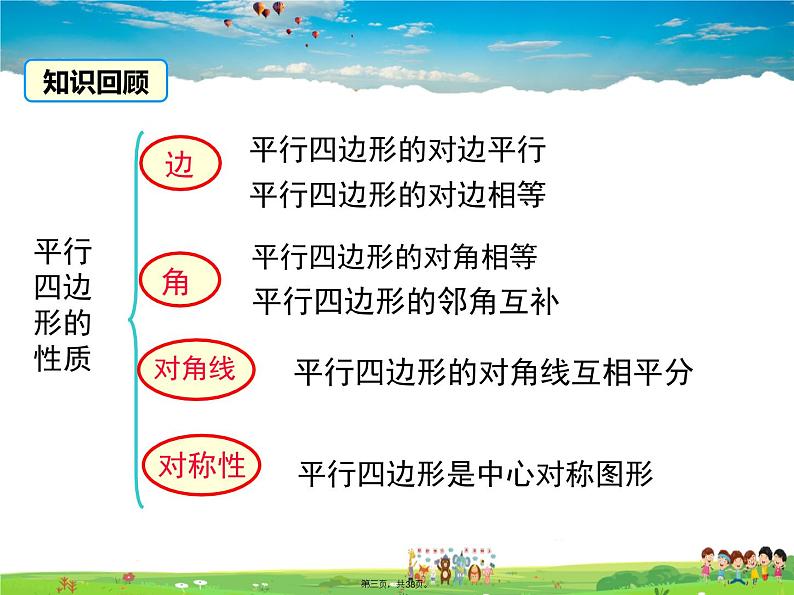
平行四边形的对角线互相平分
平行四边形是中心对称图形
学习了平行四边形之后，小明回家用细木棒钉制了一个平行四边形.第二天，小明拿着自己动手做的平行四边形向同学们展示. 小辉却问：你凭什么确定这四边形就是平行四边形呢? 大家都困惑了……
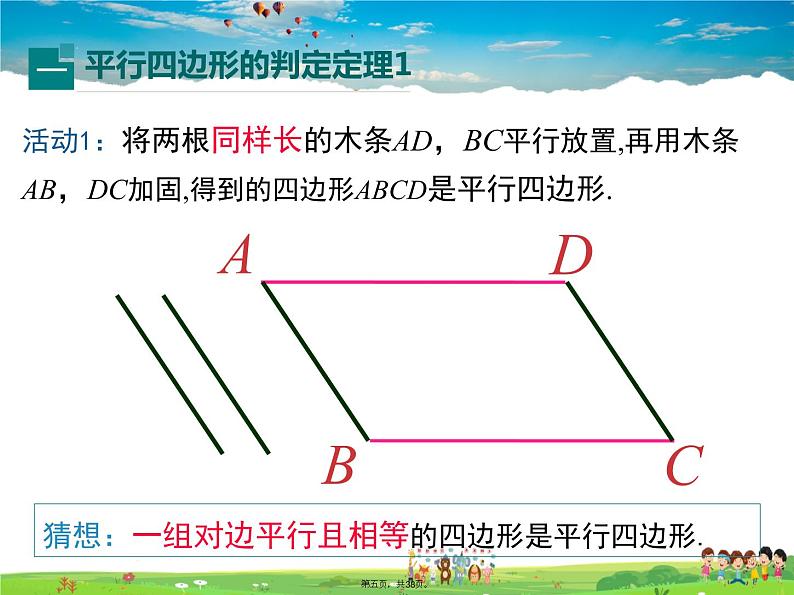
活动1：将两根同样长的木条AD，BC平行放置,再用木条AB，DC加固,得到的四边形ABCD是平行四边形.
猜想：一组对边平行且相等的四边形是平行四边形.
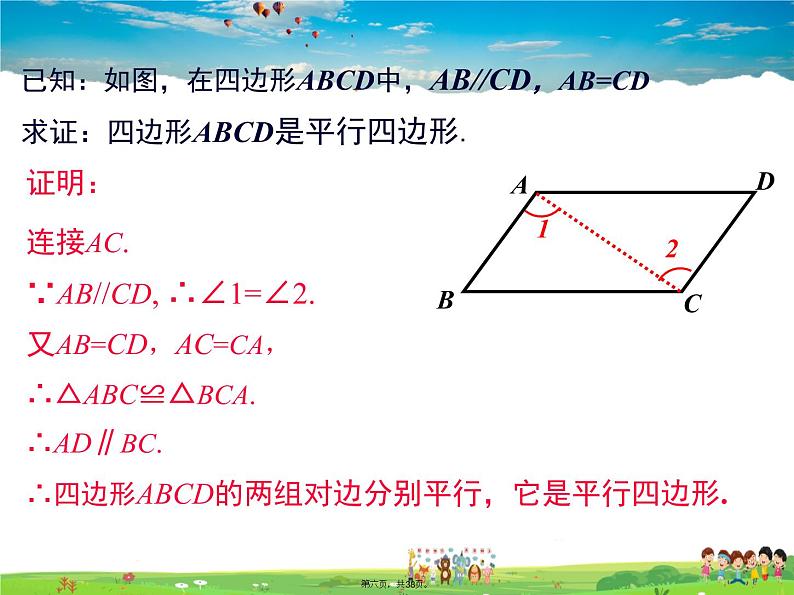
连接AC.∵AB//CD, ∴∠1=∠2.又AB=CD，AC=CA，∴△ABC≌△BCA.∴AD∥BC.∴四边形ABCD的两组对边分别平行，它是平行四边形.
已知：如图，在四边形ABCD中，AB//CD，AB=CD求证：四边形ABCD是平行四边形.
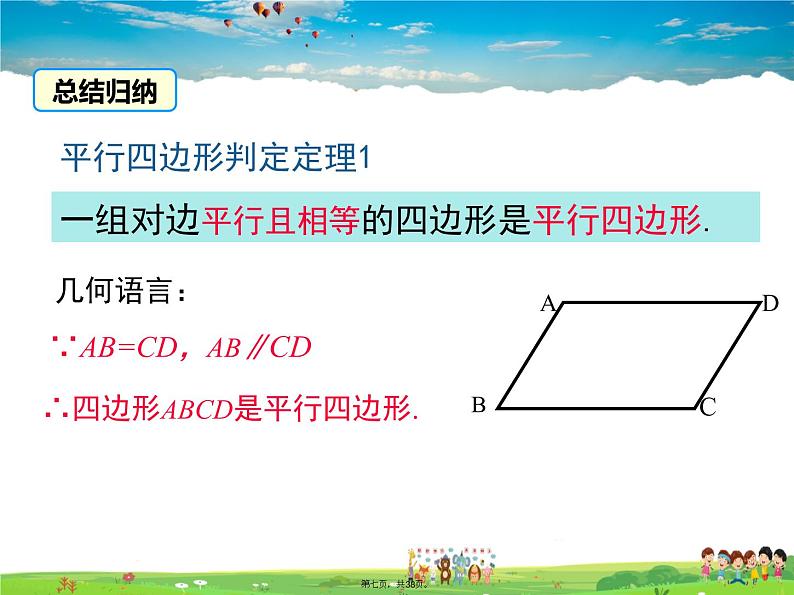
一组对边平行且相等的四边形是平行四边形.
∴四边形ABCD是平行四边形.
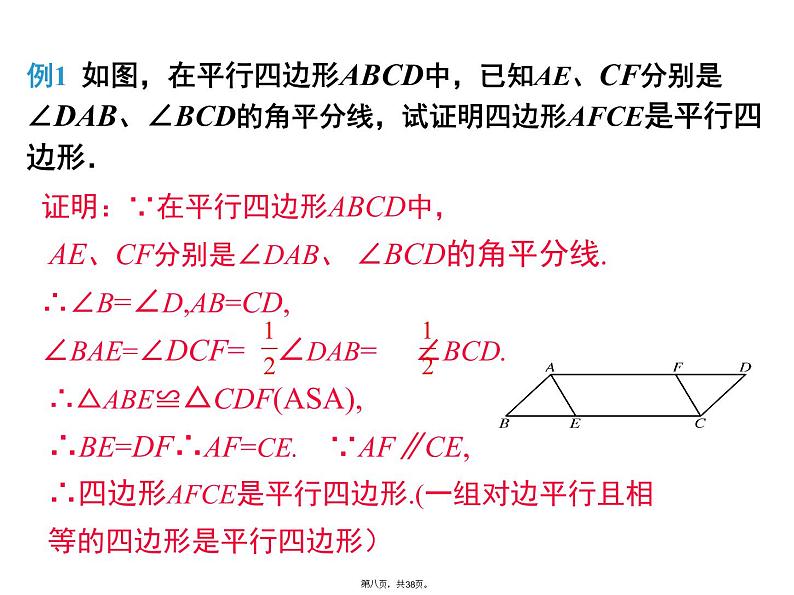
例1 如图，在平行四边形ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线，试证明四边形AFCE是平行四边形．
证明：∵在平行四边形ABCD中， AE、CF分别是∠DAB、 ∠BCD的角平分线.∴∠B=∠D,AB=CD, ∠BAE=∠DCF= ∠DAB= ∠BCD.
∴△ABE≌△CDF(ASA),∴BE=DF∴AF=CE. ∵AF∥CE,∴四边形AFCE是平行四边形.(一组对边平行且相等的四边形是平行四边形）
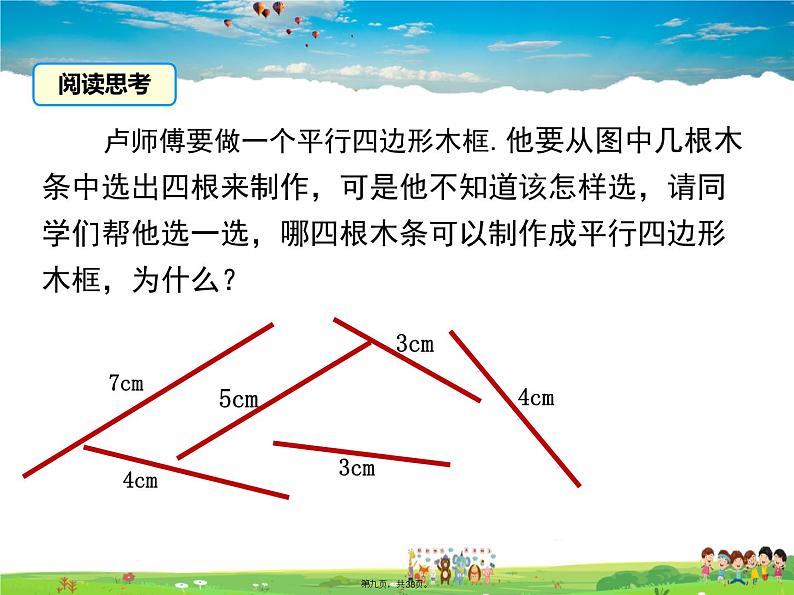
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作，可是他不知道该怎样选，请同学们帮他选一选，哪四根木条可以制作成平行四边形木框，为什么？
发现：一组对边平行，另一组对边相等的四边形不一定是平行四边形.
活动2：用两根长30cm的木条和两根长20cm的木条作为四边形的四条边，能否拼成一个平行四边形？与同伴进行交流.
猜测：两组对边分别相等的四边形是平行四边形.
已知： 四边形ABCD中，AB=CD，AD=CB.求证： 四边形ABCD是平行四边形.
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠3 , ∠ 2=∠4.
∴AB∥ CD , AD∥ CB
两组对边分别相等的四边形是平行四边形.
例2 如图，在平行四边形ABCD中，E、F分别是边BC和AD上的两点，且AF＝CE.求证：四边形AECF为平行四边形.
证明：可求得△ABE≌△CDF(SAS). ∴AE=CF.又∵AF=CE, ∴四边形ABCD是平行四边形.（两组对边分别相等的四边形是平行四边形）
将两根木条AC，BD的中点重叠，并用钉子固定，再用一根橡皮筋绕端点A，B，C，D围成一个四边形ABCD ．想一想，△AOB≌△COD吗？四边形ABCD的对边之间有什么关系？你得到什么结论？
猜想：对角线互相平分的四边形是平行四边形.
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠DCO , ∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
1.请你识别下列四边形哪些是平行四边形?
2.已知：E、F是平行四边形ABCD对角线AC上的两点，对角线BD、AC于点O，并且OE=OF.求证：四边形BFDE是平行四边形
证明： ∵四边形ABCD是平行四边形，∴ BO = DO.∵ EO = FO，∴ 四边形BFDE是平行四边形.
例3 已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
在四边形ABCD中，AO=CO，BO=DO.
∴AO-AE=CO-CF,
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形）
例4 填空：如图，在四边形ABCD中：
（1）若AB//CD，补充条件 ，使四边形ABCD为平行四边形；（2）若AB=CD，补充条件 ，使四边形ABCD为平行四边形；（3）若对角线AC、BD交于点O，OA=OC=3，OB=5，补充条件 ，使四边形ABCD为平行四边形.
第二十一页，共38页。
（4）如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，补充条件： ,使得四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
第二十二页，共38页。
思考：我们可以从角出发来判定一个四边形是否为平行四边形吗？
你能根据平行四边形的定义证明它们吗？
第二十三页，共38页。
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°.
即∠A+∠B=180°.
同理得 AB∥ CD,
定义判定：两组对角分别相等的四边形是平行四边形
第二十四页，共38页。
想一想：判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理2)
一组对边平行且相等的四边形是平行四边形（判定定理1）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）
第二十五页，共38页。
小明用手中六个全等的正三角形做拼图游戏时，拼成一个六边形．你能在图中找出所有的平行四边形吗？并说说你的理由．
解：有6个平行四边形，分别是：　 ABOF， ABCO， BCDO， CDEO， DEFO， EFAO．
第二十六页，共38页。
1.能判定四边形ABCD是平行四边形的条件：∠A:∠B:∠C:∠D的值为（　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
2. 如图所示，△ABC是等边三角形，P是其内任意一点，PD//AB,PE//BC,PF//AC,若△ABC的周长为24，则PD+PE+PF= .
3.已知AD//BC ，要使这个四边形ABCD为平行四边形，需要增加条件 .
AD=BC或AB//CD
第二十七页，共38页。
4.已知：如图，E,F分别是平行四边形ABCD 的边AD,BC的中点. 求证：BE=DF.
∵四边形ABCD是平行四边形，
∵E,F分别是AD,BC的中点，
∴四边形EBFD是平行四边形（一组对边平行并且相等的四边形是平行四边形）.
∴BE=DF(平行四边形的对边分别相等).
第二十八页，共38页。
5.已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．
∴△ABE≌△FCE（AAS）. ∴AE=EF，又∵BE=CE∴四边形ABFC是平行四边形．
解：四边形ABFC是平行四边形.理由如下：∵AB∥CD，∴∠BAE=∠CFE.∵E是BC的中点，∴BE=CE，在△ABE和△FCE中，
第二十九页，共38页。
1.现有一块等腰直角三角形铁板，要求切割一次,焊接成一个含有45°角的平行四边形 (不能有余料), 请你设计一种方案，并说明该方案正确的理由.
第三十一页，共38页。
第三十二页，共38页。
第三十三页，共38页。
2.电视剧《人民的名义》中有一位退休好干部叫陈岩石，他有一块平行四边形菜园地，夏季到来了，院子里瓜果飘香.有一天突然下起了暴雨，将菜园地的一部分冲垮，陈老的菜园地与邻居家的菜园地之间的界限看不清了，巧的是，刚好保留了顶点A和C.（1）如图，若你只有一把直尺和一个圆规，你能将图形补全吗？若能，请补全图形（不写作法，只保留作图痕迹），并证明四边形ABCD是平行四边形.
第三十四页，共38页。
（2）若E是BC边上的一点，只用一把无刻度的直尺在AD边上作点F，使得DF=BE, ①作出满足题意的点F，简要说明作图过程. ②依据你的作图，证明：DF=BE.
第三十五页，共38页。
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形（判定定理2）
第三十六页，共38页。