初中数学沪科版八年级下册19.2 平行四边形优质ppt课件

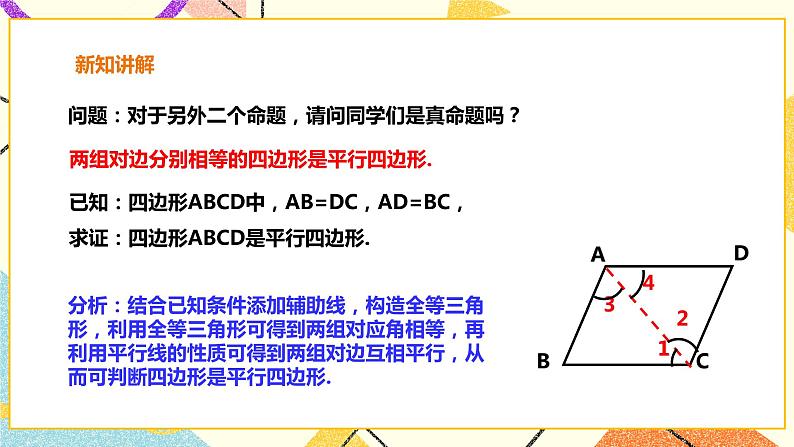
19.2.3平行四边形的判定 练习

一.选择题

1. 小明的爸爸在钉制平行四边形框架时，采用了一种方法，如图所示，将两根木条AC、BD中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（　　）

A. 对角线互相平分的四边形是平行四边形　    B. 两组对角分别相等的四边形是平行四边形 

C. 两组对边分别相等的四边形是平行四边形    D. 两组对边分别平行的四边形是平行四边形

2. 能判定四边形ABCD是平行四边形的是（　　）

A. AB∥CD，AB=CD，                     B. AB=BC，AD=CD，

C. AC=BD，AB=CD，                      D. AB∥CD，AD=CD，

3. 如图,四边形ABCD中对角线AC BD，相交于点O，下列条件不能判定这个四边形是平行四边形的是（　　）

A. ∠ABC=∠ADC, ∠BAD=∠DCB         B. AB∥CD，AB=CD

C.AB∥DC,AD∥BC                       D.AC=BD

4. 如图，在3×3的正方形网格中，以线段AB为对角线作平行四边形，使另两个顶点也在格点上，则这样的平行四边形最多可以画（　　）

A. 2个            B. 3个            C. 4个          D. 5个

5. 已知四边形ABCD中有4个条件: ①AB∥CD;②AB=CD;③BC∥AD;④BC=AD从中任选两个不能使四边形ABCD成为平行四边形的是（　　）

A. ①②         B. ①③           C. ①④         D. ②④

二.填空题

1. 已知AB∥CD，添加一个条件　　　, 使四边形ABCD为平行四边形.

2.　 如图在平面直角坐标系中，点A、B、C的坐标分别是，A(-2,5)，B(-3,-1)，C(1,-1)，在平面直角坐标系内找一点D,使得以点ABCD为顶点构成的四边形是平行四边形，那么点D的坐标是　 　　.

3.　 将两块相同的含有30度角的三角板，按图所示的方式摆放在一起，在四边形ABCD为平行四边形，请你写出判断的依据　 　　.

4.　 在三角形ABC中，∠C=90°，AC=3，AB=5若A、B、C、P四点为顶点组成一个平行四边形，则这个四边形的周长为　 　　.

三.解答题

1. 如图所示，已知在四边形ABCD中AD=BC，∠D=∠DCE，求证:四边形ABCD是平行四边形

2. 如图所示，AB∥CD,AB=CD,点E、F在BC上,且BE=CF，求证:四边形AFDE是平行四边形.

3. 如图AD=BD，AE=EC,延长DE到F, 使EF=DE,连接AF、 FC、 CD,求证:四边形DBCF是平行四边形，

参考答案

一.1.A   2.A   3.D   4.D    5.C

二.

1.AB=CD

2. (-6,5)或(2,5)或(0,-7)

3. 两组对边分别平行的四边形是平行四边形; 两组对边分别相等的四边形是平行四边形; 一组对边平行且相等的四边形是平行四边形(写出一种即可)

4.14或16或18

三

1. 证明: ∵∠D=∠DCE,

∴AD∥BC

∵AD=BC

∴四边形ABCD是平行四边形

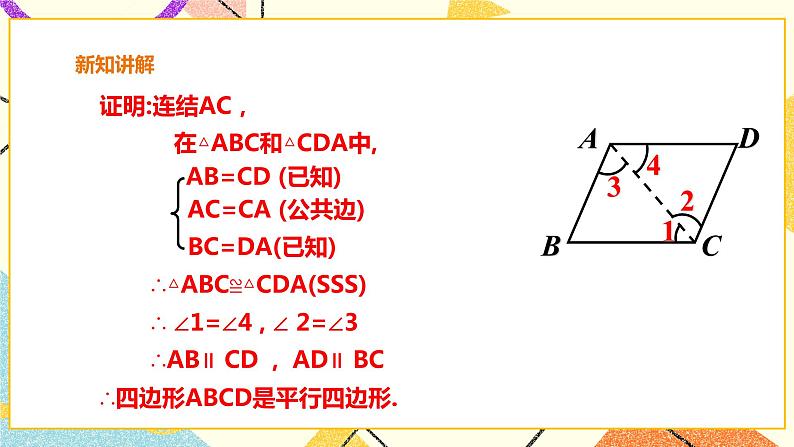
2. 证明: 连接AD交BC于点O

∵AB∥CD,

∴∠B=∠C

在△ABO和△DCO中，

∠B=∠C, ∠AOB=∠DOC,AB=CD

∴△ABO≌△DCO

∴OA=OD,OB=OC

∵BE=CF

∴OE=OF

∴四边形AFDE是平行四边形

3. 证明: ∵AD=BD，AE=EC,

∴DE∥BC

∵AE=EC,EF=DE

∴四边形ADCF是平行四边形

∴AD∥FC

即BD∥FC

∵DF∥BC

∴四边形DBCF是平行四边形