2020-2021学年19.2 平行四边形教学课件ppt

这是一份2020-2021学年19.2 平行四边形教学课件ppt，共29页。PPT课件主要包含了新课导入，分别平行，平行四边形的边角关系，怎样证明，归纳小结，两条平行线之间的距离，平行线段，随堂练习，ABCD等内容，欢迎下载使用。

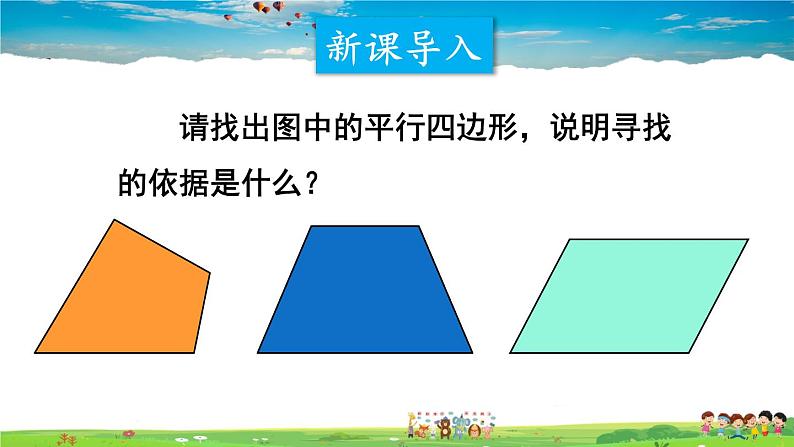
请找出图中的平行四边形，说明寻找的依据是什么？
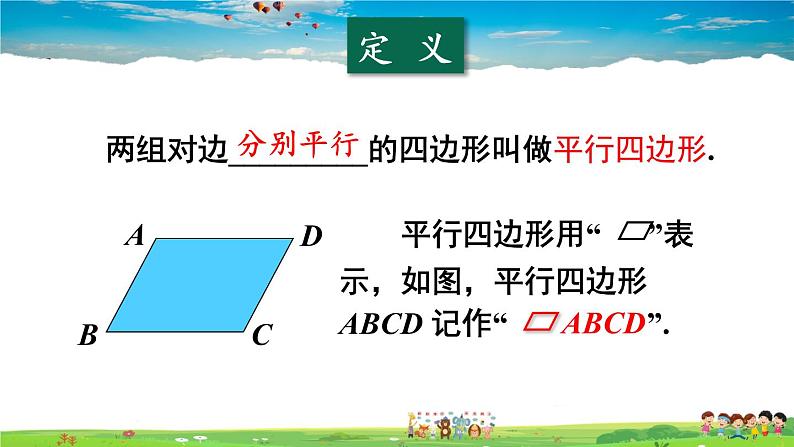
两组对边_________的四边形叫做平行四边形.
由平行四边形的定义，我们知道平行四边形的两组对边分别平行.
平行四边形还有什么性质？
猜想：平行四边形对角相等，对边相等．　　
有关四边形的问题常常转化为三角形问题解决；平行四边形的一条对角线把平行四边形分成两个全等的三角形；为此，我们通过添加辅助线，构造两个三角形，通过三角形全等进行证明.
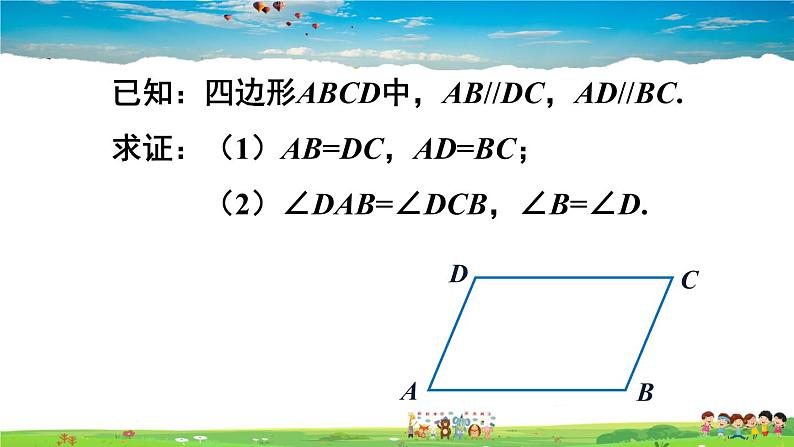
已知：四边形ABCD中，AB//DC，AD//BC.求证：（1）AB=DC，AD=BC； （2）∠DAB=∠DCB，∠B=∠D.
(1) ∵AB∥DC，AD∥BC，∴∠BAC =∠DCA，∠BCA =∠DAC.
在△ABC和△CDA中， ∠BAC =∠DCA， AC = CA， ∠BCA=∠DAC.
∴△ABC≌△CDA.（ASA）
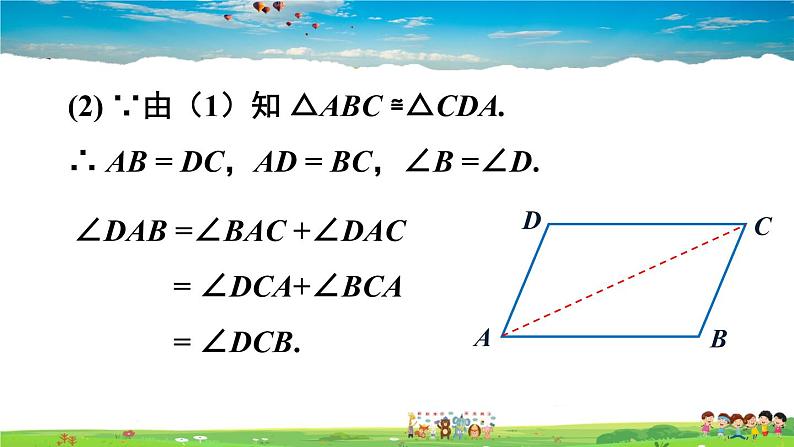
(2) ∵由（1）知 △ABC ≌△CDA.∴ AB = DC，AD = BC，∠B =∠D.
∠DAB =∠BAC +∠DAC = ∠DCA+∠BCA = ∠DCB.
性质1 平行四边形的两组对边分别相等.
性质2 平行四边形的两组对角分别相等.
例1 已知： ABCD中，BE平分∠ABC交AD于点E. （1）如果AE=2，求CD的长； （2）如果∠AEB=40°，求∠C 的度数.
解 (1) ∵BE平分∠ABC，并且AD∥BC， ∴∠ABE =∠EBC =∠AEB. ∴ AB = AE = 2.又 ∵ CD = AB， ∴ CD = 2.
(2) 由 (1)知 ∠ABE =∠AEB = 40°， ∴ ∠A = 180°－(40°+ 40°)=100°.又 ∵ ∠C = ∠A， ∴ ∠C = 100°.
直线l1//直线l2，AB，CD是夹在直线l1，l2之间的两条平行线段.
想一想：AB 是否等于CD？为什么？
由性质1 平行四边形对边相等.可得如下结论： 夹在两条平行线之间的_________相等.
由上面的结论可以知道，如果两条直线平行，那么一条直线上所有的点到另一条直线的距离都相等.
定义：两条平行线中，一条直线上任意一点到另一条直线的______叫做这两条平行线之间的距离.
例2 已知：如图□ABCD 中，AB=4，AD=5，∠B=45°. 求直线 AD 和直线 BC 之间的距离，直线 AB 和直线 DC 之间的距离.
解：过点 A 作AE⊥BC，AF⊥CD，垂足分别为点 E、点 F.
∴ 线段 AE，AF 的长分别为点 A到直线 BC 和直线 CD 的距离.
∴ 线段AE的长为直线 AD和直线 BC 之间的距离. 线段 AF 的长为直线 AB 和直线 CD 之间的距离.
∵在 Rt△ABE 中，∠AEB=90°,∠B=45°，AB=4∴∠B=∠BAE,∴BE=AE.又∵AE2+BE2=AB2∴2AE2=16.∴AE=
同理：AF= .
所以直线 AD 和直线 BC 之间的距离为 ，
直线 AB 和直线 CD 之间的距离为 .
例3 已知：如图，过 △ABC 的三个项点，分别作对边的平行线，这三条直线两两相交，得 △A′B′C′ . 求证：△ABC 的顶点分别是△A′B′C′ 三边的中点.
分析如图，要证明点 A 是 B′C′ 的中点，只要证明AB′ = AC′.
证明：∵AB∥B′C，BC∥AB′ ， ∴AB′ = BC.同理：AC′ = BC, ∴AB′ = AC′.同理：BC′ = BA′，CA′ = CB′.所以 △ABC 的顶点分别是△A′B′C′ 三边的中点.
解：∵四边形ABCD为平行四边形， ∴∠A+∠B=180°，∠A=∠C，∠B=∠D. 又∵∠A∶∠B=2∶3， ∴∠A=∠C=72°，∠B=∠D=108°.
解：∵四边形 ABCD 为平行四边形，∴AB = CD，AD = BC. 又∵C ABCD = AB+BC+CD+AD = 28cm，且 AB∶BC = 3∶4，∴AB = CD = 6cm，AD = BC = 8cm.
3. 如图，在 中，已知 AD = 8 cm，AB = 6 cm，DE 平分∠ADC 交 BC 边于点 E，则BE的长为________.
4. 平行四边形的一条角平分线分对边为 3 和4 两部分，求平行四边形的周长.
解 如图，∵ ABCD中，
AD∥BC，∴∠1=∠3，又∠1=∠2，∴∠2=∠3，∴AB=BE.当BE=3时，AB=BE=3，∴ ABCD的周长为：（AB+BC）×2=（3+7）×2=20.
当BE=4时，AB=BE=4，∴ ABCD的周长为：（AB+BC）×2=（4+7）×2=22.