



数学沪科版19.2 平行四边形一等奖ppt课件
展开1.理解并掌握平行四边形的概念.2.探索并掌握平行四边形对边相等、对角相等的性质.3.能运用平行四边形的性质进行有关的证明和计算,通过将平行四边形问题转化为三角形问题,体会数学转化思想.4.通过观察、度量、猜想、证明平行四边形的性质,体会几何研究的思路和方法,培养学生逻辑推理能力.
小学我们已经认识了平行四边形,你能从下面的视频中找到这样的图形吗?
在生活中, 你还能举出具有平行四边形形象的实例吗?
通过上述实例,你还记得什么样的图形叫做平行四边形吗?
两组对边分别平行的四边形叫做平行四边形.
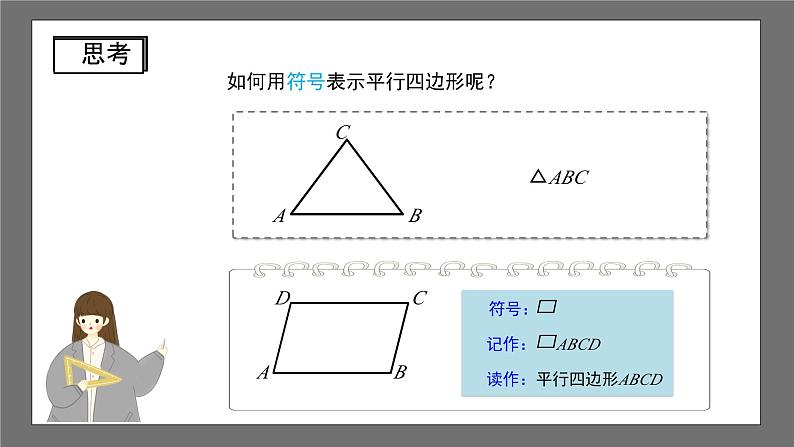
如何用符号表示平行四边形呢?
记作: ABCD
读作:平行四边形ABCD
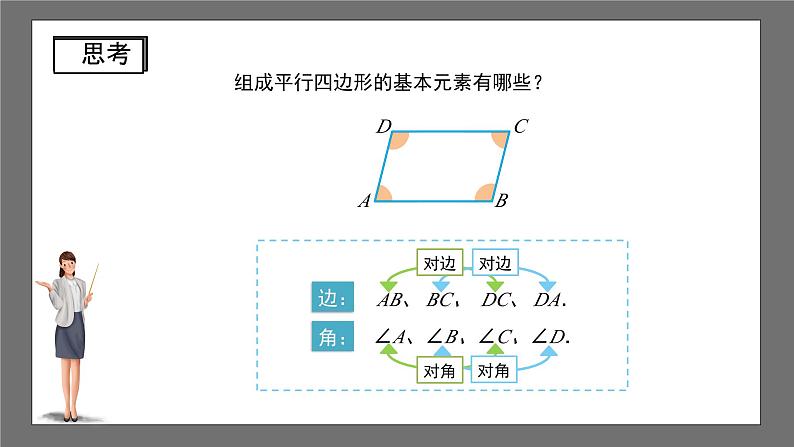
AB、 BC、 DC、 DA.
组成平行四边形的基本元素有哪些?
∠A、∠B、∠C、∠D.
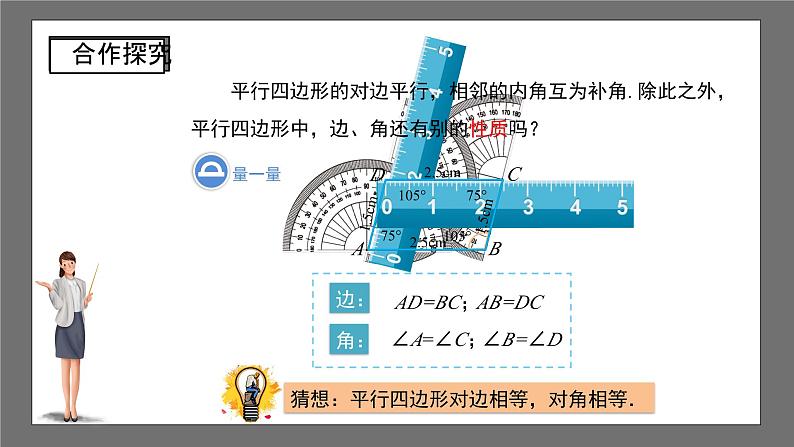
猜想:平行四边形对边相等,对角相等.
平行四边形的对边平行,相邻的内角互为补角. 除此之外,平行四边形中,边、角还有别的性质吗?
你能证明你的猜想吗?
已知:如图,四边形ABCD中,AB∥DC,AD∥BC.求证:(1) AB=DC , AD=BC; (2)∠DAB=∠DCB,∠B=∠D.
AB∥DC AD∥BC
AB=CD , AD=BC
AB=CD,AD=BC
∠BAC+∠DAC =∠DCA+∠BCA
(1)∵AB∥DC,AD∥BC,
∴∠BAC=∠DCA,∠BCA=∠DAC.
在△ABC和△CDA中,
∴△ABC≌△CDA.(ASA)
∴AB=DC,AD=BC.
(2)由(1)知 △ABC≌△CDA
∠DAB=∠BAC+∠DAC
激动人心的时刻马上要开始了,纸笔都准备好喽~
性质1 平行四边形的对边相等.性质2 平行四边形的对角相等.
∵四边形ABCD是平行四边形∴AD=BC,AB=DC ∠A=∠C,∠B=∠D
(1)∵ BE平分∠ABC,
∴∠ABE=∠EBC.
∴∠AEB=∠EBC=∠ABE.
又∵CD=AB,∴CD=2.
(2)由(1)知 ∠AEB=∠ABE=40°
∴∠A=180° (40°+40°)=100°
又∵∠C=∠A,∴∠C=100°.
想一想:如图,直线l1∥l2,AB,CD是夹在直线l1,l2之间的两条平行线段.请探究AB与CD的数量关系?并说明理由.
∵ l1 ∥ l2,AB∥CD,
∴四边形ABDC是平行四边形.
AE与CF有怎样的数量关系呢?
过点A作AE⊥BC,AF⊥CD,垂足分别为点E、点F,
∴线段AE、AF的长分别为点A到直线BC和直线CD的距离.
∴线段AE长为直线AD和直线BC之间的距离,
线段AF长为直线AB和直线CD之间的距离.
在Rt△ABE中,∠AEB=90°,∠B=45°,
又∵AE²+BE²=AB²,
例3. 已知:如图,过△ABC的三个顶点,分别作对边的平行线,这三条直线两两相交,得△ABC.求证:△ABC的顶点分别是△ABC三边的中点.
∵AB∥BC,BC∥AB,
同理BC= BA, CA= CB.
所以△ABC的顶点分别是△ABC三边的中点.
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D(平行四边形的对角相等).
∴∠C=60°,∠B=180°∠A=120°.
∴∠D=∠B=120°.
2.已知:如图,在平行四边形ABCD中, E,F 是对角线AC上的两点,且AE=CF.求证:BE = DF.
∵四边形ABCD是平行四边形 ∴AB = CD AB // CD ∴∠BAE=∠DCF 又∵AE=CF ∴△BAE≌△DCF(SAS) ∴BE=DF
教科书第78页练习2,3.
数学八年级下册19.2 平行四边形评课ppt课件: 这是一份数学八年级下册<a href="/sx/tb_c70401_t3/?tag_id=26" target="_blank">19.2 平行四边形评课ppt课件</a>,共20页。PPT课件主要包含了平行四边形的性质,平行四边形,一级标题,ABC,ADBC,∠A∠C,ABDC,∠B∠D,∠DAB∠DCB,平行四边形问题等内容,欢迎下载使用。
初中数学沪科版八年级下册19.2 平行四边形多媒体教学课件ppt: 这是一份初中数学沪科版八年级下册19.2 平行四边形多媒体教学课件ppt,共12页。PPT课件主要包含了平行四边形的性质,新知应用,应用提高,这节课你学到了什么,作业布置等内容,欢迎下载使用。
初中数学沪科版八年级下册19.2 平行四边形图文课件ppt: 这是一份初中数学沪科版八年级下册19.2 平行四边形图文课件ppt,共16页。PPT课件主要包含了知识回顾,新知探究,平行四边形的性质3,典型例题,课堂练习,<AD<9,课下作业,挑战自我等内容,欢迎下载使用。













