初中数学人教版八年级上册13.1.1 轴对称教学课件ppt

这是一份初中数学人教版八年级上册13.1.1 轴对称教学课件ppt，共24页。PPT课件主要包含了情境导入，轴对称和轴对称图形，轴对称的性质，全班总动员，辩一辩，线段垂直平分线的定义，图形轴对称的性质，轴对称图形的性质等内容，欢迎下载使用。

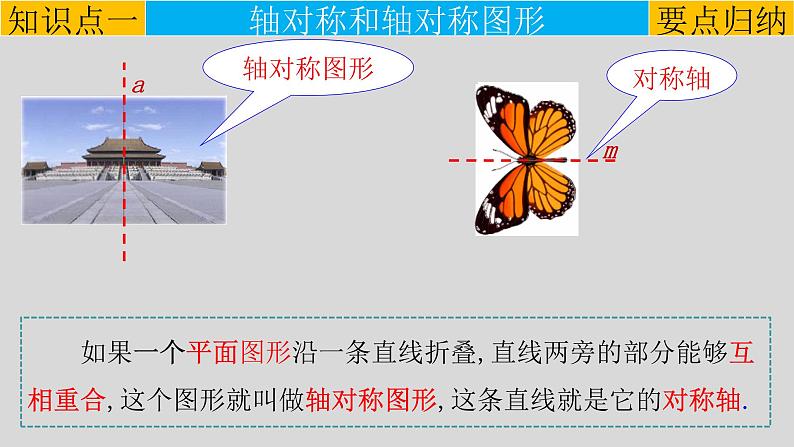
它们有什么共同的特点？
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
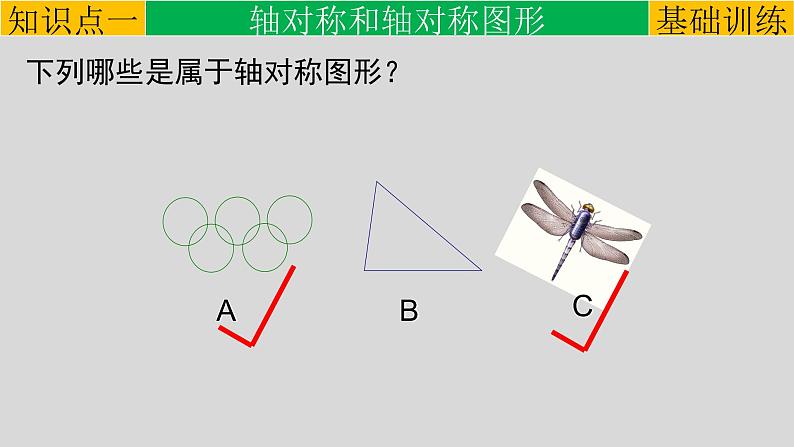
下列哪些是属于轴对称图形？
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z游戏规则:每人轮流按顺序报一个字母.如果你认为你所报的字母的形状是一个轴对称图形,你就迅速站起来报出,并说出它有几条对称轴；如果你认为你报的字母的形状不是轴对称图形,那么,你只需坐在座位上报就可以了.其他同学认真听,如果报错了,及时提醒.
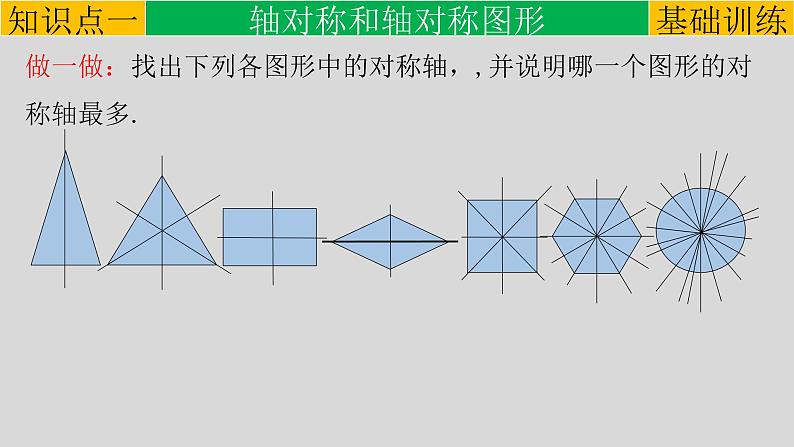
做一做：找出下列各图形中的对称轴，,并说明哪一个图形的对称轴最多.
想一想：下面的每对图形有什么共同特点？
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
【例1】下列四组图片中有哪几组图形成轴对称？
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
1.这是轴对称图形还是两个图形成轴对称？
2.找出下文中成轴对称的文字：一叶孤舟,坐着两三个骚客,启用四桨五帆,经过六滩七湾,历尽八颠九簸,可叹十分来迟.十年寒窗,进了九八家书院,抛却七情六欲,苦读五经四书,考了三番两次,今天一定要中.
3.想一想：一辆汽车的车牌在水中的倒影如图所示,你能确定该车的车牌号码吗?
【思考】如图,△ABC和△A´B´C´关于直线MN对称,点A´,B´,C´分别是点A,B,C的对称点,线段AA´,BB´,CC´与直线MN有什么关系？
AA´⊥MN，BB´⊥MN，CC´⊥MN.
如图,MN⊥AA´,AP=A´P.直线MN是线段AA´的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
类似地，轴对称图形的对称轴，是任何一对对称点所连线段的垂直平分线.
如图，MN垂直平分AA ′, MN垂直平分BB ′.
【例2-1】如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD＝150º,∠B＝40º,则∠BCD的度数是(　　) A.130º B.150º C.40º D.65º
方法归纳：轴对称是一种全等变换，在轴对称图形中求角度时，一般先根据轴对称的性质及已知条件，得出相关角的度数，然后再结合多边形的内角和或三角形外角的性质求解.
【例2-2】如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为(　　) A.4cm2 B.8cm2 C.12cm2 D.16cm2
解析：根据正方形的轴对称性可得，阴影部分的面积等于正方形ABCD面积的一半，∵正方形ABCD的边长为4cm,∴S阴影＝42÷2＝8(cm2).故选B.
方法归纳：正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
1.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是(　　) A.AB∥DF B.∠B=∠E C.AB=DE D.AD的连线被MN垂直平分 2.如图,Rt△ABC中,∠ACB=90º,∠A=50º,将其折叠,使点A落在边CB上A´处,折痕为CD,则∠A´DB的度数为_____.
3.如图,O为△ABC内部一点,OB＝3,P、R为O分别以直线AB、BC为对称轴的对称点．(1)请指出当∠ABC是什么角度时,会使得PR的长度等于6?并完整说明PR的长度为何在此时等于6的理由.
解：(1)如图,∠ABC=90º时,PR=6.证明如下：连接PB、RB，∵P,R为O分别以直线AB,BC为对称轴的对称点，∴PB=OB=3,RB=OB=3.∵∠ABC=90º,∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90º,∴∠PBR=180º,即P、B、R三点共线，∴PR=PB+RB=3+3=6；
(2)承(1)小题,请判断当∠ABC不是你指出的角度时,PR的长度小于6还是大于6?并完整说明你判断的理由.
解：PR的长度小于6,理由如下：∵∠ABC≠90º,则点P、B、R三点不在同一直线上,∴PB＋BR＞PR.∵PB＋BR＝2OB＝2×3＝6，∴PR＜6.