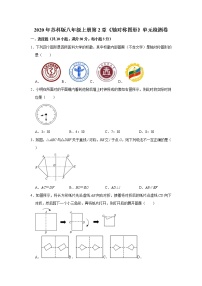
2021学年第二章 轴对称图形综合与测试练习题

这是一份2021学年第二章 轴对称图形综合与测试练习题，共16页。


A.1 B.2 C.3 D.4
【答案】C
【解析】其中第一、三、四既是轴对称图形又是中心对称图形，第二个图形只是轴对称图形，故选C.
2.如图，已知，以两点为圆心，大于的长为半径画圆，两弧相交于点，连接与相较于点，则的周长为（ ）
A．8B．10C．11D．13
【答案】A
【解析】由作法得MN垂直平分AB，∴DA=DB，
∴△BDC的周长=DB+DC+BC=DA+DC+BC=AC+BC=5+3=8．
故选A．
3.要使得△ABC是等腰三角形，则需要满足下列条件中的（ ）
A．∠A=50°，∠B=60°B．∠A=50°，∠B=100°
C．∠A+∠B=90° D．∠A+∠B=90°
【答案】D
【解析】解：A、∵∠A=50°，∠B=60°，∴∠C=180°-∠A-∠B=70°，
所以∠A≠∠B≠∠C，
所以△ABC不是等腰三角形；
B、∵∠A=50°，∠B=100°，∴∠C=180°-∠A-∠B=30°，
所以∠A≠∠B≠∠C，所以△ABC不是等腰三角形；
C、∠A+∠B=90°不能判定△ABC是等腰三角形；
D、∠A+∠B=90°，则2∠A+∠B=180°，
∵∠A+∠B+∠C=180°，∴∠A=∠C，
所以△ABC是等腰三角形．
故选D．
4.如图是屋架设计图的一部分，其中∠A=30°，点D是斜梁AB的中点，BC、DE垂直于横梁AC，AB=16m，则DE的长为（ ）．
A．8 mB．4 mC．2 mD．6 m
【答案】B
【解析】解：∵∠A=30°，AB=16m，∠ACB=90°，∴BC=AB=×16=8m，
∵BC、DE垂直于横梁AC，∴BC//DE，
∵点D是斜梁AB的中点，∴AE=CE∴DE=BC=×8=4m．
故选B．
5.如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，下列结论：①；②；③∠BDE＝∠BAC；④BE＝DE；⑤，其中正确的个数为（ ）
A．5个B．4个C．3个D．2个
【答案】B
【解析】解：①正确，∵在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，
∴CD＝ED；
②正确，因为由HL可知△ADC≌△ADE，所以AC＝AE，即AC＋BE＝AB；
③正确，因为∠BDE和∠BAC都与∠B互余，根据同角的余角相等，所以∠BDE＝∠BAC；
④错误，因为∠B的度数不确定，故BE不一定等于DE；
⑤正确，因为CD＝ED，△ABD和△ACD的高相等，所以S△BDE：S△ACD＝BE：AC．
故正确的个数为4个.
6.如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是( )秒
A．2.5B．3C．3.5D．4
【答案】D
【解析】解：设运动的时间为x，
在△ABC中，AB=20cm，AC=12cm，
点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，
当△APQ是等腰三角形时，AP=AQ，AP=20﹣3x，AQ=2x，即20﹣3x=2x，
解得x=4．
故选D．
二．填空题（每小题2分，共20分）
7.如图，与关于直线l对称，则∠的度数为_____．
【答案】20°
【解析】解：∵△ABC与△A′B′C′关于直线l对称，
∴∠A′=∠A=50°，
在△A′B′C′中，∠C′=180°﹣∠A′﹣∠B′
=180°﹣50°﹣110°
=20°．
故答案为20°．
8.如图，点P关于OA、OB的对称点分别为C、D，连结CD，交OA于M，交OB于N，若△PMN的周长=8厘米，则CD为_______厘米
【答案】8
【解析】解：根据题意点P关于OA、OB的对称点分别为C、D，
故有MP=MC，NP=ND；
则CD=CM+MN+ND=PM+MN+PN=8cm．
故答案为8．
9.如图所示，在中，，，于，则__________.
【答案】3
【解析】，，于,
所以BD=DC,所以BD=3.
10.已知一个等腰三角形的一边是6,另一边是8,则这个等腰三角形的周长是____.
【答案】20或22
【解析】解：若6为等腰三角形的腰长，则8底边的长，
此时等腰三角形的周长=6+6+8=20；
若8为等腰三角形的腰长，则6为底边的长，
此时等腰三角形的周长=8+6+8=22；
则等腰三角形的周长为20或22．
故答案是：20或22
11.如图的4×4的正方形网格中，有A、B、C、D四点，直线a上求一点P，使PA+PB最短，则点P应选____点（C或D）．
【答案】C．
【解析】如图，点A′是点A关于直线a的对称点，连接A′B，则A′B与直线a的交点，即为点P，此时PA+PB最短，
∵A′B与直线a交于点C，
∴点P应选C点．
故答案为C．
12.如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C.若P是BC边上一动点，则DP长的最小值为_______．
【答案】4
【解析】如图，过点D作DE⊥BC于点E，当DP=DE时，DP最小，
∵BD⊥DC，∠A=90°，
∴∠DEB=∠DEC=90°=∠A，∠BDC=90°，
∴∠C+∠CDE=90°，∠CDE+∠BDE=90°，
∴∠BDE=∠C，
又∵∠ADB=∠C，
∴∠ADB=∠BDE，
∴在△ABD和△EBD中 ，
∴DE=AD=4，
即DP的最小值为4.
13.已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA，垂足为点E，且直线DE交OB于点F，如图所示．若DE＝2，则DF＝_____．
【答案】4．
【解析】过点D作DM⊥OB，垂足为M，如图所示．
∵OC是∠AOB的平分线，∴DM＝DE＝2．
在Rt△OEF中，∠OEF＝90°，∠EOF＝60°，
∴∠OFE＝30°，即∠DFM＝30°．
在Rt△DMF中，∠DMF＝90°，∠DFM＝30°，
∴DF＝2DM＝4．
故答案为4．
14.如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，AD恰好平分∠BAC，若DE＝1，则BC的长是_____．
【答案】3
【解析】解：∵AD平分∠BAC，且DE⊥AB，∠C＝90°，∴CD＝DE＝1，
∵DE是AB的垂直平分线，∴AD＝BD，∴∠B＝∠DAB，
∵∠DAB＝∠CAD，∴∠CAD＝∠DAB＝∠B，
∵∠C＝90°，∴∠CAD+∠DAB+∠B＝90°，∴∠B＝30°，
∴BD＝2DE＝2，∴BC＝BD+CD＝1+2＝3，
故答案为3．
15.如图，在△ABC中，AB=AC，∠A=120°，BC=9cm，AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，则MN的长为______cm．
【答案】3

【解析】连接AM，AN，∵AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，
∴BM=AM，CN=AN，∴∠MAB=∠B，∠CAN=∠C，∵∠BAC=120°，AB=AC，∴∠B=∠C=30°，
∴∠BAM+∠CAN=60°，∠AMN=∠ANM=60°，∴△AMN是等边三角形，∴AM=AN=MN，∴BM=MN=NC，
∵BC=9cm，∴MN=3cm．
故答案为3cm．
16.△ABC中，AB=AC，∠BAC=30°，△ABC的面积为49，P为直线BC上一点，PE⊥AB，PF⊥AC，CH⊥AB，垂足分别为E，F，H．若PF=3，则PE=________
【答案】4或10
【解析】
∵PE⊥AB，PF⊥AC，CH⊥AB，
∴
∵在△ACH中,∠A=30°，
∴AC=2CH，
∵
∴CH⋅CH=49，
∴CH=7，
①P为底边BC上一点，如图①,
∵+=，
∴
又∵AB=AC，
∴PE+PF=CH，
∴PE=CH−PF=7−3=4；
②P为BC延长线上的点时，如图②,
∵-=
∴
又∵AB=AC，
∴PE-PF=CH，
∴PE=3+7=10.
故答案为4或10.
三．解答题（共68分）
17.（10分）认真观察图①中的四个图中阴影部分构成的图案,其中每个小正方形的边长为1,回答下列问题:

(1)请写出这四个图案都具有的两个特征.
特征1:___________
特征2:____________
(2)请在图②中设计一个你心中最美丽的图案,使它也具备你所写出的上述特征
【答案】(1)都是轴对称图形 面积都为4；（2）作图见解析.
【解析】（1）根据图示可知都是轴对称图形，阴影部分的面积都为4，由此可得答案；
（2）根据轴对称图形的概念按要求进行作图即可得.
试题解析：（1）都是轴对称图形，面积都为4，
故答案为都是轴对称图形，面积都为4；
（2）如图所示：
18.（8分）作图题：（要求保留作图痕迹，不写作法）
（1）作△ABC中BC边上的垂直平分线EF（交AC于点E，交BC于点F）；
（2）连结BE，若AC=10，AB=6，求△ABE的周长．
【答案】（1）答案见解析；（2）16．
【解析】解：(1)如图所示，
(2)∵EF垂直平分BC，
∴BE=EC，
∴△ABE的周长=AB+BE+AE=AB+BE+EC=AB+BC，
∵AB=6，BC=10，
∴△ABE的周长=6+10=16．

19.（10分）如图，已知CD⊥AB于点D，BE⊥AC于点E，CD交BE于点O.
(1)若OC=OB，求证：点O在∠BAC的平分线上；
(2)若点O在∠BAC的平分线上，求证：OC=OB．
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)连接AO，
∵CD⊥AB，BE⊥AC，
∴∠CEB=∠BDO=90°，
又∵∠COE=∠BOD（对顶角相等），
∴∠C=∠B（等角的余角相等），
∴在△CEO和△BDO中，
，
∴△CEO≌△BDO（ASA），
∴OE=OD（全等三角形的对应边相等），
又∵CD⊥AB，BE⊥AC，
∴点O在∠BAC的平分线上；
(2)∵AO平分∠BAC，CD⊥AB，BE⊥AC，
∴OD=OE，
在△DOB和△EOC中，
，
∴△DOB≌△EOC（ASA），
∴OB=OC．
20.（10分）如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
【答案】（1）∠BOE+∠COF=50°；（2）12cm.
【解析】解:(1)∵EF∥BC,
∴∠OCB=∠COF,∠OBC=∠BOE.
又∵BO,CO分别是∠BAC和∠ACB的角平分线,
∴∠COF=∠FCO=∠ACB=30°,∠BOE=∠OBE=∠ABC=20°.
∴∠BOE+∠COF=50°.
(2)∵∠COF=∠FCO,∴OF=CF.
∵∠BOE=∠OBE,∴OE=BE.
∴△AEF的周长=AF+OF+OE+AE=AF+CF+BE+AE=AB+AC=8 cm.
∴△ABC的周长=8+4=12(cm).
21.（8分）已知，如图，是的平分线，，点在上，，，垂足分别是、.试说明：.
【答案】见详解
【解析】证明：∵BD为∠ABC的平分线，
∴∠ABD=∠CBD，
在△ABD和△CBD中，

∴△ABD≌△CBD（SAS），
∴∠ADB=∠CDB，
∵点P在BD上，PM⊥AD，PN⊥CD，
∴PM=PN．
22.（10分）如图，已知在中，，为边的中点，过点作，，垂足分别为，.
（1）求证：；
（2）若，，求的周长.
【答案】（1）见解析；（2）12
【解析】（1）证明: ∵DE⊥AB,DF⊥A，∴∠BED=∠CFD=90°，
∵AB=AC，∴∠C=∠B，
∵D是BC的中点，∴.BD=CD，
在△BED和△CFD中,
,
∴△BED≌△CFD，∴DE=DF ；
（2）解：∵AB=AC, ∠A=60°，
∴△ABC为等边三角形，∴∠B=60°，
∵∠BED=90°，∴∠BDE=30°，∴，
∵BE=1，∴BD=2，∴BC=2BD=4.​∴△ABC的周长为12.
23.（12分）如图（1），在中，的平分线交边于点D．

（1）求证：为等腰三角形；
（2）若的平分线交边于点E，如图（2），求证：；
（3）若外角的平分线交的延长线于点E，请你探究（2）中的结论是否仍然成立，若不成立，请写出正确的结论，并说明理由．
【答案】（1）见解析；（2）见解析；（3）不成立，正确结论：，理由见解析
【解析】（1）【证明】在中，，，
∴．
∵平分，∴，∴，∴，
∴为等腰三角形．
（2）【证明】如图（1），在上截取，连接．
由（1）得为等腰三角形，∴，∴．
∵平分，∴，∴，
∴，∴，
∴，∴，∴，∴．
（3）【解】不成立，正确结论：．
理由：如图（2），在上截取，连接．
∵由（1）得，∴．
∵，∴．
∵平分，∴，
∴，，∴，则．
∵，∴，
∴，
∴．