人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称精品课时训练

这是一份人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称精品课时训练，文件包含1311轴对称原卷版doc、1311轴对称解析版doc等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

13.1.1轴对称


一、单选题
1．如图，直线，相交于点．为这两直线外一点，且．若点关于直线，的对称点分别是点，，则，之间的距离可能是（ ）

A．0 B．5
C．6 D．7
【答案】B
【分析】连接根据轴对称的性质和三角形三边关系可得结论．
【详解】连接，如图，

∵是P关于直线l的对称点，
∴直线l是的垂直平分线，
∴
∵是P关于直线m的对称点，
∴直线m是的垂直平分线，
∴
当不在同一条直线上时，
即
当在同一条直线上时，
故选：B
【点评】此题主要考查了轴对称变换，熟练掌握轴对称变换的性质是解答此题的关键
2．下列四个图形分别是节能、节水、绿色食品和低碳标志，其中轴对称图形是（ ）
A． B． C． D．
【答案】C
【分析】根据轴对称图形的概念对各选项分析判断即可得到答案．
【详解】A.不是轴对称图形，故本选项错误；
B.不是轴对称图形，故本选项错误；
C.是轴对称图形，故本选项正确；
D.不是轴对称图形，故本选项错误．
故选：C．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形沿着对称轴折叠后可完全重合即为轴对称图形．
3．如图，在中，，将沿直线翻折，点落在点的位置，则的度数是（ ）

A． B． C． D．
【答案】C
【分析】由折叠可知，，再根据三角形的外角等于与它不相邻的两个内角的和分别表示出和，进而得出，最终得出答案．
【详解】如图，

如图，设直线与分别交于点，点，
令与的交点为，且，
沿直线翻折，点落在点上，
，
在中，，
在中，，
，
，

即
故选：C．
【点评】本题主要考查了翻折变换与三角形外角性质得综合应用，熟练掌握三角形外角性质是解答本题的关键．
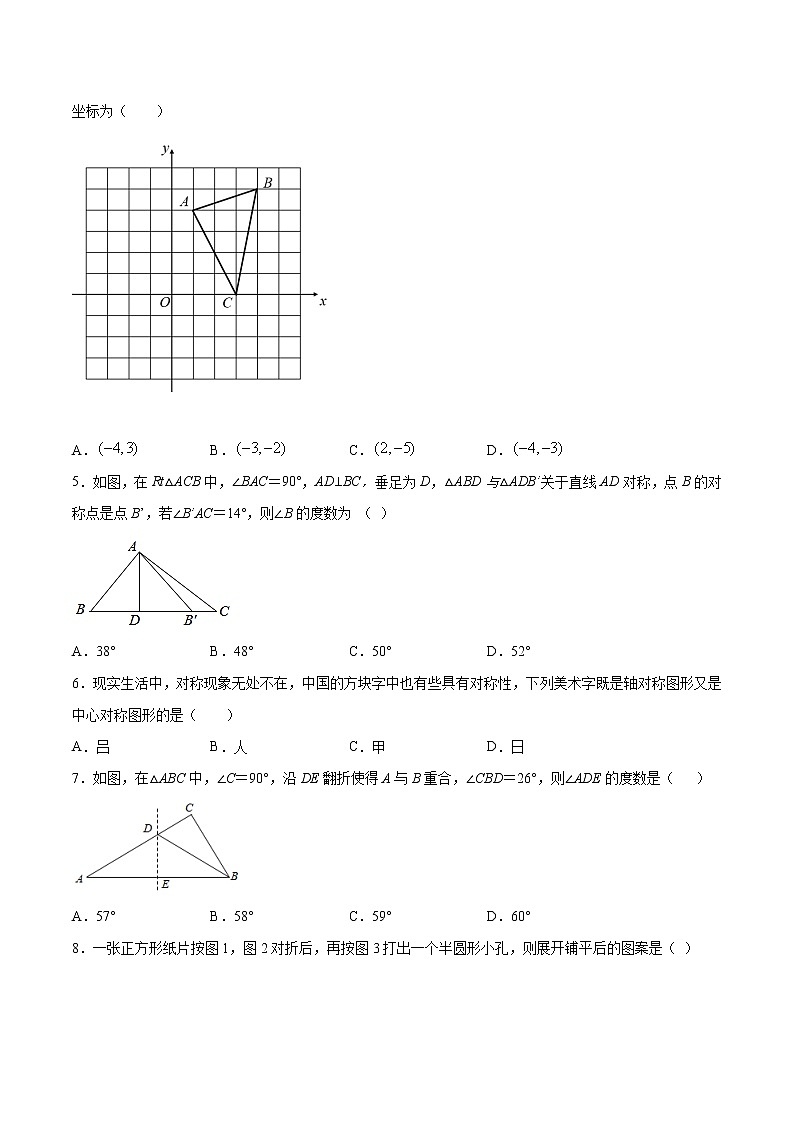
4．是网格中的格点三角形（三角形的各顶点都在网格的交叉点上），如图建立直角坐标系，将该三角形先向下平移2个单位，然后再将平移后的图形沿y轴翻折，得到，则点B对应点的坐标为（ ）


A． B． C． D．
【答案】A
【分析】根据网格求出点B坐标，向下平移2个单位，点 B的横坐标不变，纵坐标减2得对应点B1的坐标，再沿y轴翻折，横坐标变为相反数，纵坐标不变即可得出点B′（-4，3）．
【详解】∵点B坐标为（4，5）
向下平移2个单位，得点B对应点的坐标B1（4，5-2），即B1（4，3），
再沿y轴翻折，
点B′（-4，3），
故选择A．
【点评】本题考查根据平面直角坐标系写出点的坐标，平移的性质，轴对称性质，掌握平面直角坐标系点的坐标构成，平移的性质，轴对称性质是解题关键．
5．如图，在Rt△ACB中，∠BAC＝90°，AD⊥BC，垂足为D，△ABD与△ADB’关于直线AD对称，点B的对称点是点B’，若∠B’AC＝14°，则∠B的度数为 （ ）

A．38° B．48° C．50° D．52°
【答案】D
【分析】由对称的性质得，根据∠BAC＝90°可得，再根据直角三角形两锐角关系求解即可．
【详解】∵△ABD与△ADB’关于直线AD对称，
∴
∵∠BAC＝90°，∠B’AC＝14°
∴
∴
∴
故选D．
【点评】本题考查了轴对称的性质以及直角三角形两锐角关系，掌握轴对称的性质是本题的关键．
6．现实生活中，对称现象无处不在，中国的方块字中也有些具有对称性，下列美术字既是轴对称图形又是中心对称图形的是（　　）
A．吕 B．人 C．甲 D．日
【答案】D
【分析】根据轴对称图形与中心对称图形的概念求解．
【详解】A、“吕”字是轴对称图形，不是中心对称图形，故本选项不合题意；
B、“人”字是轴对称图形，不是中心对称图形，故本选项不合题意；
C、“甲”字是轴对称图形，不是中心对称图形，故本选项不合题意；
D、“日”字既是轴对称图形，又是中心对称图形，故本选项符合题意．
故选：D．
【点评】本题主要考查了轴对称图形与中心对称图形的判断，准确分析是解题的关键．
7．如图，在△ABC中，∠C＝90°，沿DE翻折使得A与B重合，∠CBD＝26°，则∠ADE的度数是（ ）

A．57° B．58° C．59° D．60°
【答案】B
【分析】求出∠CDB的度数，再根据翻折求出∠ADE的度数即可．
【详解】∵∠C＝90°，∠CBD＝26°，
∴∠CDB=90°-∠CBD＝64°，
∴∠ADB=116°，
由翻折可知，∠ADE=∠BDE=58°；
故选：B．
【点评】本题考查了轴对称和三角形内角和，解题关键是明确翻折角相等的性质，熟练运用三角形内角和解决问题．
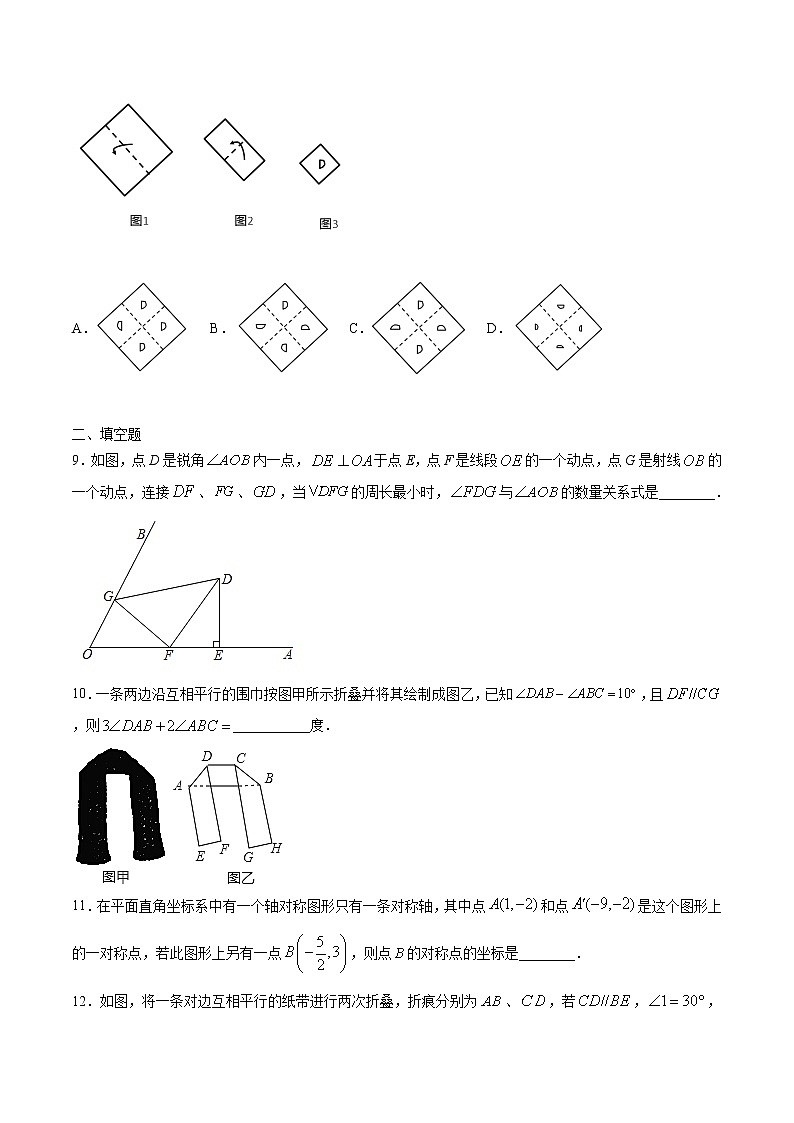
8．一张正方形纸片按图1，图2对折后，再按图3打出一个半圆形小孔，则展开铺平后的图案是（ ）


A． B． C． D．
【答案】D
【分析】依据轴对称的性质，将纸片依次展开还原，即可得到正确结论．
【详解】将图3展开可得小孔位于图2中虚线的左右两侧，且关于该虚线对称；
把图2展开可得小孔位于图1中虚线的上下两侧，且关于该虚线对称；
故选：D．
【点评】本题主要考查了剪纸问题．解决这类问题要熟知轴对称图形的特点，关键是准确的找到对称轴．一般方法是动手操作，拿张纸按照题目的要求剪出图案，展开即可得到正确的图案．


二、填空题
9．如图，点D是锐角内一点，于点E，点F是线段的一个动点，点G是射线的一个动点，连接、、，当的周长最小时，与的数量关系式是________．

【答案】
【分析】作D关于OA的对称点D′，作D关于OB的对称得D″，连接D′D″，交OA、OB于F、G，此时△DFG的周长最小，最小值为D′D″，连OD、OD′、OD″，根据轴对称的性质得出△GOD≌△GOD″，△FOD≌△FOD′，即可得出∠BOD=∠BOD′，∠ODG=∠OD″G，∠DOA=∠AOD′，∠ODF=∠ODF′，由∠D′OD″=2∠AOB，∠GDF=∠ODF′+∠ODG″根据三角形内角和定理即可得出2∠AOB+∠GDF=180°．
【详解】作D关于OA的对称点D′，作D关于OB的对称得D″，连接D′D″，交OA、OB于F、G，此时△DFG的周长最小，最小值为D′D″，连OD、OD′、OD″，

由轴对称的性质可知，△GOD≌△GOD″，△FOD≌△FOD′，
∴∠BOD=∠BOD″，∠ODG=∠OD″G，∠DOA=∠AOD′，∠ODF=∠OD′F，
∴∠D′OD″=2∠AOB，∠GDF=∠OD′F+∠OD″G，
∵∠D′OD″+∠OD′F+∠OD″G=180°，
∴2∠AOB+∠GDF=180°，
故答案为2∠AOB+∠GDF=180°．
【点评】本题考查了轴对称-最短路线问题，熟练掌握轴对称的性质是解题的关键．
10．一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙，已知，且，则___________度．

【答案】230
【分析】将围巾展开，根据折叠的性质得：则∠ADM=∠ADF，∠KCB=∠BCN，设∠ABC=x，根据平行线的性质得：∠FDC=∠KCG=2x，由平角的定义列式：∠FDC+∠FDM=180°，可得x的值，从而得结论．
【详解】如图乙，将围巾展开，则∠ADM=∠ADF，∠KCB=∠BCN，

设∠ABC=x，则∠DAB=x+10°，
∵CD∥AB，
∴∠ADM=∠DAB=x+10°=∠ADF，
∵DF∥CG，
∴∠FDC=∠KCG=2x，
∵∠FDC+∠FDM=180°，
∴2x+2（x+10°）=180°，
x=40°，
∴3∠DAB+2∠ABC=3（x+10°）+2x=5x+30°=230°，
故答案为：230．
【点评】此题考查了平行线性质，解题时注意：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
11．在平面直角坐标系中有一个轴对称图形只有一条对称轴，其中点和点是这个图形上的一对称点，若此图形上另有一点，则点的对称点的坐标是________．
【答案】
【分析】先根据点 A(1,−2) 和点 A′(−9,−2) 是这个图形上的一对称点找到相应的对称关系，再根据该对称关系找到点 B 的对称点的坐标即可．
【详解】∵点 A(1,−2) 和点 A′(−9,−2) 是这个图形上的一对称点，
∴点A与点 A′关于直线x=−4对称，
∴点 B(,3)关于直线x=−4对称为（），
故答案为： ．
【点评】此题考查轴对称的性质和轴对称与坐标的变化，找到对称轴是关键，难度一般．
12．如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为、，若，，则的大小为_______度．

【答案】60
【分析】由折叠的性质可得∠3=∠1=30°，从而求得∠4=120°，再根据平行线的性质定理求出∠ACD=∠4=120°，最后再根据平行线性质定理求出∠2=60°．
【详解】如图，延长FA，由折叠的性质，可得∠3=∠1=30°，

∴∠4=180°-30°-30°=120°，
∵CD∥BE，BE∥AF，
∴∠ACD=∠4=120°，
又∵AC∥BD，
∴∠2=180°-∠ACD=180°-120°=60°．
故答案为：60．
【点评】本题考查了平行线的性质，解题的关键是根据平行线的性质找出图中角度之间的关系．
13．将一条两边互相平行的纸带沿折叠，如图（1），，，设

（1）_______（用含x的代数式表示）
（2）若将图1继续沿折叠成图（2），________（用含x的代数式表示）．
【答案】
【分析】（1）由平行线的性质得，，折叠和三角形的外角得，，最后计算出；
（2）由折叠和平角的定义求出，再次折叠经计算求出 ．
【详解】（1）如图1所示：

，
，，
又，
，
又，
，
又，

；
（2）如图2所示：

，
，
又，



故答案为：（1）；（2）．
【点评】本题综合考查了平行线的性质，折叠问题，等腰三角形的性质，三角形的外角定理，平角的定义和角的和差等相关知识，重点掌握平行线的性质，难点是折叠前后的变及不变的问题，二次折叠角的前后大小等量关系．
14．如图，的斜边在x轴上，，C在第一象限，，是线段上的动点，过点P作的垂线a，以直线a为对称轴，线段进行轴对称变换后得线段．

（1）当点和点C重合时，m的值为______________．
（2）当线段与线段没有公共点时，m的取值范围是___________．
【答案】 或
【分析】（1）根据折叠的性质可知，当点与点重合时，点是的中点，过点作于点，求出和的长，依此可得点坐标，再根据中点坐标公式即可求解；
（2）分线段在线段的上面和线段在线段的下面两种情况讨论即可求解．
【详解】（1）过点作于点．
在中，，，
，，
在中，，，
，
点坐标为，，点坐标为，
当点与点重合时，点坐标为，，
的值为；
（2）线段在线段的上方，
，
，
，
，
则；
线段在线段的下方，
．
综上所述，或．
故答案为：；或．

【点评】本题考查了翻折变换（折叠问题），涉及的知识点有：折叠的性质，中点坐标公式，以及分类思想的运用．

三、解答题
15．如图，数轴上、、三个数所对应的点分别为、、，已知，与距离2个单位，与距离6个单位．


（1）①直接写出数、的值；
②求代数式的值；
（2）若将数轴折叠，使得点与点重合，求与点重合的点表示的数．
【答案】（1）①，；②4；（2）5
【分析】（1）①根据数轴上两点间的距离可求；②将代数式利用完全平方公式化简后，将a、b的值代入后可求；
（2）根据轴对称的性质，设点B与点M重合，利用线段的中点的性质，求出线段DM的长度即可求出点M表示的数．
【详解】（1）①∵
∴，．
②原式=．
（2）设AC的中点为D．
∵AC=AB+BC=2+6=8，
∴．
∴．
设折叠后点B与点M重合，且点M表示的数为m，如图所示．

∴．
∴．
∴．
∴与点重合的点表示的数5．
【点评】本题考查了数轴、求代数式的值、轴对称等知识点，熟知数轴上两点间的距离的计算和轴对称的性质是解题的关键．
16．如图，与关于直线对称，与的交点在直线上．若，，，．

（1）求出的长度；
（2）求的度数．
【答案】（1）＝3cm；（2）＝18°
【分析】（1）根据△ABC与△ADE关于直线MN对称确定对称点，从而确定对称线段相等即BC＝ED，即可求出的值；
（2）根据△ABC与△ADE关于直线MN对称，利用轴对称的性质得出对称角∠EAD＝∠BAC，即可解决问题；
【详解】（1）∵△ABC与△ADE关于直线MN对称，ED＝4cm，FC＝1cm，
∴BC＝ED＝4cm，
∴BF＝BC−FC＝3cm．
（2）∵△ABC与△ADE关于直线MN对称，∠BAC＝76°，∠EAC＝58°，
∴∠EAD＝∠BAC＝76°，
∴∠CAD＝∠EAD−∠EAC＝76°−58°＝18°．
【点评】本题考查轴对称的性质，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
17．已知：如图，是一个长方形的台球面，有、两球分别位于图中所在位置，试问怎样撞击球，才能使先碰到台边反弹后再击中球？在图中画出球的运动线路．

【答案】见解析
【分析】首先作出点A关于FC的对称点，再连接交FC于点P，连接AP，PB，可得A球的运动路线．
【详解】如图所示：运动路线：．

【点评】本题主要考查生活中的轴对称现象，关键是掌握轴对称的性质．
18．如图，在平面直角坐标系中，A (-1， 4)， B(3， 2)， C(-1，0)

(1) 点A关于y轴的对称点的坐标为 ，点B关于x轴的对称点的坐标为 ， 线段AC的垂直平分线与y轴的交点D的坐标为 ．
(2)求(1)中的△的面积．
【答案】（1） 、、；（2）5；
【分析】（1）依据对称的性质可得点的坐标；然后利用垂直平分线的性质可得点D的坐标；
（2）如图所示，将补为直角梯形，直角梯形面积，即可；
【详解】（1）由题知点关于y对称的点为，由对称性质可得：点的坐标：；
同理可得点于x对称的点为，由对称性质可得：点的坐标：；
又AC的垂直平分线为：y=2，与y轴的交点为D，∴ 点；
（2）将补为直角梯形，如下图所示：

∴ ；；
；
∴；
【点评】本题考查平面坐标、对称的性质及不规则三角形的面积，关键不规图形的面积割补求法；
19．已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG，将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．
（1）如图1，若点F与点G重合，求∠MEN的度数；
（2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；

【答案】（1）90°；（2）105°．
【分析】（1）由对折得EN平分∠AEF，EM平分∠BEF，可得∠NEF＝∠AEF，∠MEF＝∠BEF，从而可得：∠MEN＝∠NEF+∠MEF＝（∠AEF+∠BEF）＝∠AEB，结合平角的定义可得答案；
（2）由对折可得EN平分∠AEF，EM平分∠BEG，证明∠NEF＝∠AEF，∠MEG＝∠BEG，可得∠NEF+∠MEG＝（∠AEF+∠BEG）＝（∠AEB﹣∠FEG），从而可得答案．
【详解】（1）∵EN平分∠AEF，EM平分∠BEF
∴∠NEF＝∠AEF，∠MEF＝∠BEF
∴∠MEN＝∠NEF+∠MEF＝∠AEF+∠BEF＝（∠AEF+∠BEF）＝∠AEB
∵∠AEB＝180°
∴∠MEN＝×180°＝90°
（2）∵EN平分∠AEF，EM平分∠BEG
∴∠NEF＝∠AEF，∠MEG＝∠BEG
∴∠NEF+∠MEG＝∠AEF+∠BEG＝（∠AEF+∠BEG）＝（∠AEB﹣∠FEG）
∵∠AEB＝180°，∠FEG＝30°
∴∠NEF+∠MEG＝（180°﹣30°）＝75°
∴∠MEN＝∠NEF+∠FEG+∠MEG＝75°+30°＝105°．
【点评】本题考查的是轴对称的性质，角的和差，平角的定义，掌握以上知识是解题的关键．
20．如图，、分别是的边、上的点，在上求作一点，使的周长最小，并说明你这样作的理由．

【答案】见解析
【分析】由于△PMN的周长=PM+MN+PN，而PM是定值，故只需在在AC上找一点N，使MN+PN最小即可，作点P关于直线AC的对称点P′，连接MP′交直线AC于点N，则此时△MNP的周长最小．
【详解】作点P关于直线AC的对称点P′，连接MP′交直线AC于点N，则PN=P′N，

由于△PMN的周长=PM+MN+PN，而PM是定值，故只需在在AC上找一点N，使MN+PN最小即可；
∵此时MN+PN=MN+P′N=MP′，MN+PN最小，
∴此时△PMN的周长最小，最小值等于PM+P′M．
【点评】本题考查的是轴对称-最短路线问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．
21．尺规作图（只保留作图痕迹，不要求写出作法及证明过程）：如图，已知点在内，分别在、边上求作点和点，使的周长最小．

【答案】见解析
【分析】步骤：①作P关于AB的对称点P1．②作P关于BC的对称点P2．③连接P1P2．④P1P2与AB的交点就是E，P1P2与BC的交点就是F．即为所求．
【详解】如图：即为所求，

注：①作关于的对称点；
②作关于的对称点；
③连接P1P2．
④P1P2与AB的交点就是E，P1P2与BC的交点就是F．
【点评】本题考查了作图-复杂作图，轴对称等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
22．如图，四边形ABCD中，AD∥BC，DC⊥BC，将四边形沿对角线BD折叠，点A恰好落在DC边上的点E处，若∠EBC=20°，求∠EBD的度数．

【答案】
【分析】根据AD∥BC，DC⊥BC，∠EBC=20°，再利用三角形外角的性质，可求得∠DEB的度数，由折叠的性质，可得：∠A=∠DEB=110°，∠ABD=∠EBD，继而求得∠EBD的度数．
【详解】∵AD∥BC，DC⊥BC，
∴∠C=90°，
∵∠EBC=20°，
∴∠DEB=∠EBC +∠C=20°+90°=110°，
由折叠的性质可得：∠A=∠DEB =110°，∠ABD=∠EBD，
∵AD∥BC，
∴∠ABC=180°-∠A=180°-110°=70°，
∴∠EBD=．
【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．