初中数学浙教版八年级上册2.6 直角三角形课前预习ppt课件

这是一份初中数学浙教版八年级上册2.6 直角三角形课前预习ppt课件，共14页。PPT课件主要包含了①②③，等腰直角等内容，欢迎下载使用。

第二课时 直角三角形的判定
1．(4分)在△ABC中，若∠A∶∠B∶∠C＝1∶2∶3，则△ABC是(　　)A．锐角三角形　　　　 B．直角三角形C．钝角三角形 D．等腰三角形2．(4分)若一个三角形的三条高线交点恰好是此三角形的一个顶点，则此三角形一定是(　　)A．等腰三角形 B．等边三角形C．等腰直角三角形 D．直角三角形
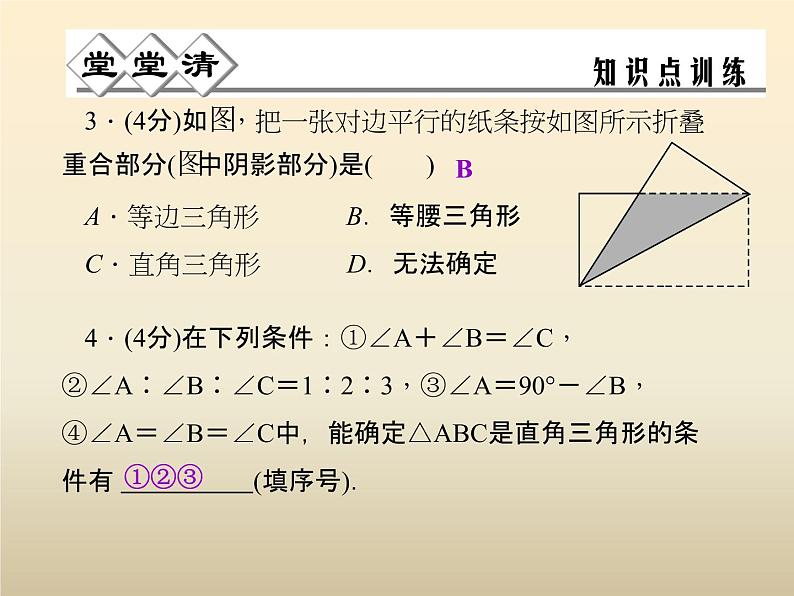
3．(4分)如图，把一张对边平行的纸条按如图所示折叠，重合部分(图中阴影部分)是(　　)A．等边三角形 B．等腰三角形C．直角三角形 D．无法确定
4．(4分)在下列条件：①∠A＋∠B＝∠C，②∠A∶∠B∶∠C＝1∶2∶3，③∠A＝90°－∠B，④∠A＝∠B＝∠C中，能确定△ABC是直角三角形的条件有 (填序号)．
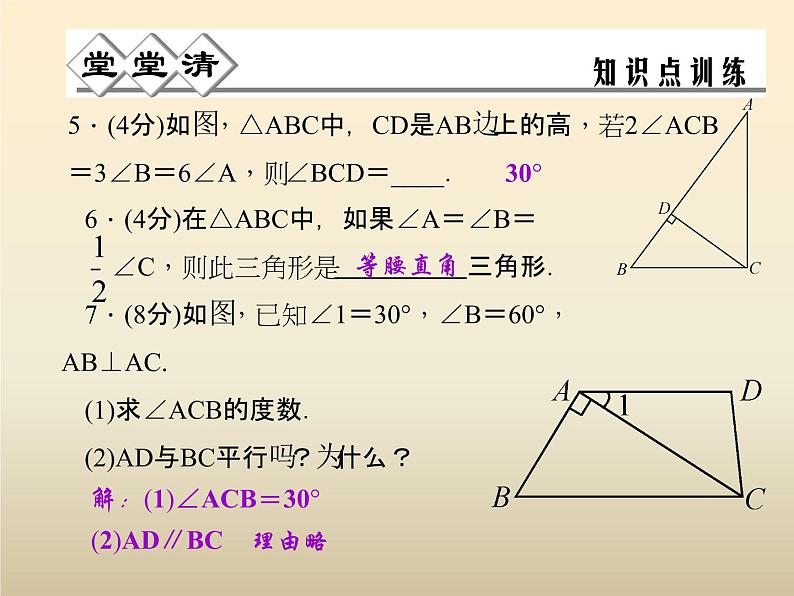
5．(4分)如图，△ABC中，CD是AB边上的高，若2∠ACB＝3∠B＝6∠A，则∠BCD＝____．
6．(4分)在△ABC中，如果∠A＝∠B＝ ∠C，则此三角形是 三角形．7．(8分)如图，已知∠1＝30°，∠B＝60°，AB⊥AC.(1)求∠ACB的度数．(2)AD与BC平行吗？为什么？
解：(1)∠ACB＝30°(2)AD∥BC　理由略
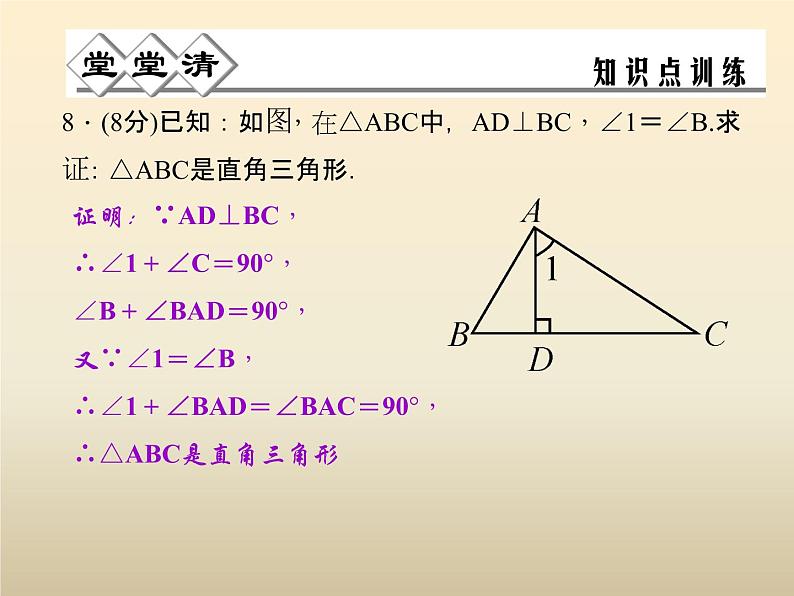
8．(8分)已知：如图，在△ABC中，AD⊥BC，∠1＝∠B.求证：△ABC是直角三角形．
证明：∵AD⊥BC，∴∠1＋∠C＝90°，∠B＋∠BAD＝90°，又∵∠1＝∠B，∴∠1＋∠BAD＝∠BAC＝90°，∴△ABC是直角三角形
9．(10分)在△ABC中，∠A与∠C的和是∠B的2倍，∠C与∠A的差等于∠B.求证：△ABC为直角三角形．证明：∵∠A＋∠B＋∠C＝180°，∠A＋∠C＝2∠B，∠C－∠A＝∠B，∴∠C＝90°，∠B＝60°，∠A＝30°，∴△ABC为直角三角形
10．(4分)如图，把等腰直角△ABC沿BD折叠，使点A落在边BC上的点E处．下面结论错误的是(　　)A．AB＝BE　　　　　B．AD＝DCC．AD＝DE D．AD＝EC
11．(4分)如图，在△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F.现给出以下四个结论：①AE＝CF；②△EPF是等腰直角三角形；③EF＝AP；④S四边形AEPF＝ S△ABC.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A，B重合)，上述结论中始终正确的是(　　)A．①②③ B．①②④C．②③④ D．①③④
12．(4分)如图，△ABC中，∠ACB＝90°，AB＝8 cm，D是AB的中点．现将△BCD沿BA方向平移1 cm，得到△EFG，FG交AC于点H，则GH的长等于____cm.
13．(8分)如图，在△ABC中，∠ACB＝90°，CD，CE三等分∠ACB，CD⊥AB.求证：AB＝2BC.
证明：由∠ACB＝90°，CD，CE三等分∠ACB，CD⊥AB，可得AE＝CE，CE＝BE＝BC，∴AB＝2BC
14．(8分)如图，∠CAD＝90°，∠ABD＝2∠EBC，AD∥BC，求证：DE＝2AB.
15．(10分)如图，△ABC是等边三角形，D为边BC延长线一点，且AC＝CD，试说明△ABD是直角三角形．
证明：∵AC＝CD，∴∠CAD＝∠CDA，∵△ABC是等边三角形，∴∠BCA＝∠BAC＝60°，∵∠CAD＋∠D＝∠BCA，AC＝CD，∴2∠CAD＝∠BCA＝60°，∠CAD＝∠D，∴∠CAD＝30°，∠BAD＝∠BAC＋∠CAD＝60°＋30°＝90°，∴△ABD是直角三角形．