初中数学浙教版八年级上册第2章 特殊三角形2.4 等腰三角形的判定定理集体备课课件ppt

这是一份初中数学浙教版八年级上册第2章 特殊三角形2.4 等腰三角形的判定定理集体备课课件ppt，共14页。PPT课件主要包含了第5题图，第6题图，等角对等边，解∠A＝21°等内容，欢迎下载使用。

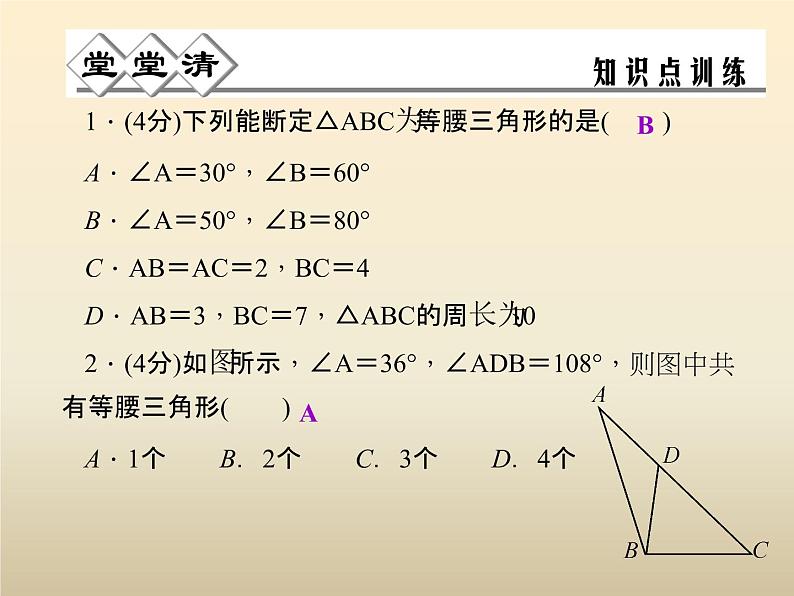
1．(4分)下列能断定△ABC为等腰三角形的是(　　)A．∠A＝30°，∠B＝60°B．∠A＝50°，∠B＝80°C．AB＝AC＝2，BC＝4D．AB＝3，BC＝7，△ABC的周长为102．(4分)如图所示，∠A＝36°，∠ADB＝108°，则图中共有等腰三角形(　　)A．1个　　B．2个　　C．3个　　D．4个
3．(4分)如果一个三角形的一内角平分线与对边垂直，那么这个三角形一定是(　　)A．等腰三角形 B．锐角三角形C．直角三角形 D．钝角三角形4．(4分)已知同一平面内有三条直线l1，l2，l3，若l1⊥l2，l2⊥l3，则l1与l3的位置关系是(　　)A．平行 B．相交C．垂直 D．以上都不对
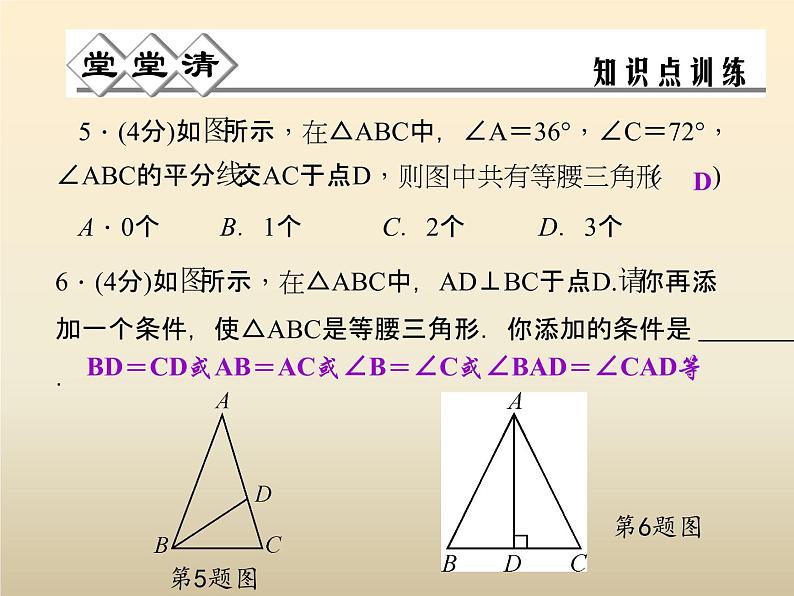
5．(4分)如图所示，在△ABC中，∠A＝36°，∠C＝72°，∠ABC的平分线交AC于点D，则图中共有等腰三角形(　　)A．0个 B．1个 C．2个 D．3个
6．(4分)如图所示，在△ABC中，AD⊥BC于点D.请你再添加一个条件，使△ABC是等腰三角形．你添加的条件是 ．
BD＝CD或AB＝AC或∠B＝∠C或∠BAD＝∠CAD等
7．(6分)试说明：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：∠CAE是△ABC的外角，AD平分∠CAE，AD∥BC(如图所示)．求证：AB＝AC.证明：∵AD∥BC(已知)，∴∠1＝∠B( )，∠2＝∠C( )．又∵AD平分∠CAE(已知)，∴∠1＝∠2(角平分线的定义)，∴∠B＝∠C(等量代换)．∴AB＝AC( )．
两直线平行，同位角相等
两直线平行，内错角相等
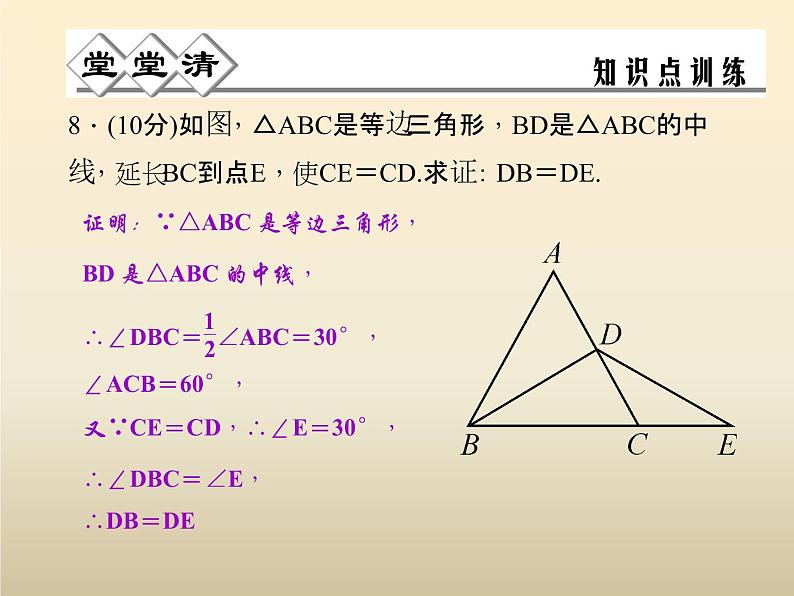
8．(10分)如图，△ABC是等边三角形，BD是△ABC的中线，延长BC到点E，使CE＝CD.求证：DB＝DE.
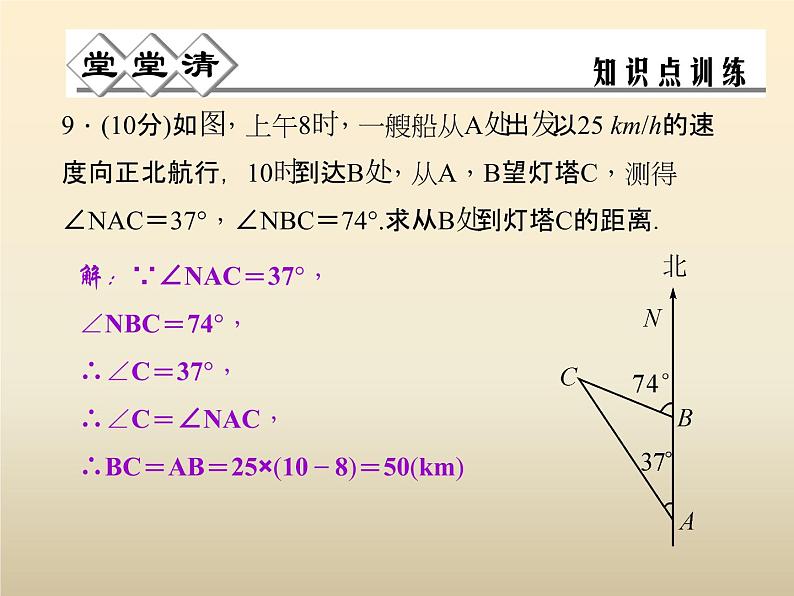
9．(10分)如图，上午8时，一艘船从A处出发以25 km/h的速度向正北航行，10时到达B处，从A，B望灯塔C，测得∠NAC＝37°，∠NBC＝74°.求从B处到灯塔C的距离．
解：∵∠NAC＝37°，∠NBC＝74°，∴∠C＝37°，∴∠C＝∠NAC，∴BC＝AB＝25×(10－8)＝50(km)
10．(4分)如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于点M，交AC于点N，若BM＋CN＝9，则线段MN的长为(　　)A．6　　　B．7　　　C．8　　　D．9
11．(4分)如图所示，P是等边三角形ABC内一点，将△ABP绕点B顺时针方向旋转60°，得到△CBP′，若PB＝3，则PP′＝____．
12．(10分)如图，在△ABC中，点E在AB上，点D在BC上，BD＝BE，∠BAD＝∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．
解：△AFC是等腰三角形，理由略
13．(10分)如图，点B，D在射线AM上，点C，E在射线AN上，且AB＝BC＝CD＝DE，已知∠EDM＝84°，求∠A的度数．
14．(10分)已知：如图，锐角△ABC的两条高BE，CD相交于点O，且OB＝OC.(1)求证：△ABC是等腰三角形；(2)判断点O是否在∠BAC的角平分线上，并说明理由．
解：(1)略 (2)点O在∠BAC的角平分线上，理由略
15．(12分)课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张纸片都是等腰三角形．你能办到吗？请画出示意图说明剪法．我们有多种剪法，图1是其中的一种方法：
定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；(若两种方法分得的三角形成3对全等三角形，则视为同一种)(2)△ABC中，∠B＝30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD＝BD，DE＝CE.设∠C＝x°，试画出示意图，并求出x的所有可能的值．