2021学年4.3 实数评课ppt课件

这是一份2021学年4.3 实数评课ppt课件，共15页。PPT课件主要包含了有理数，无理数，无限不循环小数，无理数的由来等内容，欢迎下载使用。

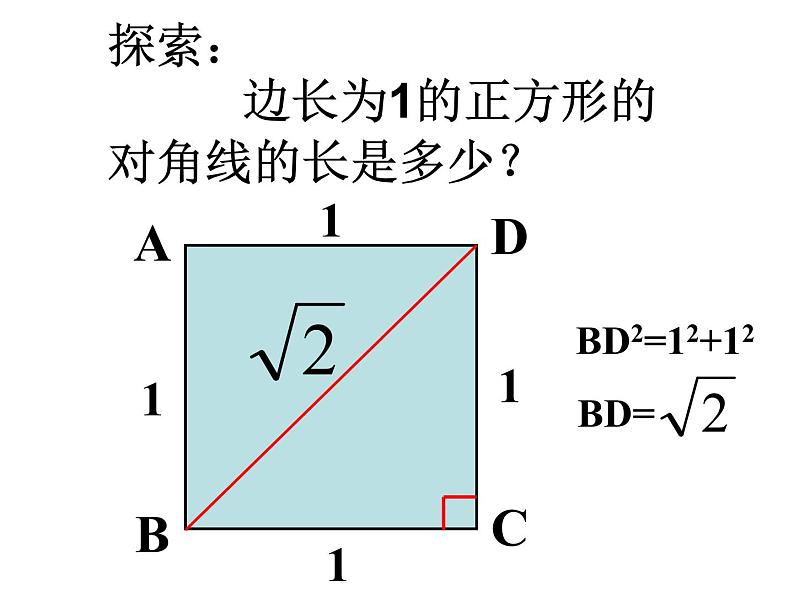
探索： 边长为1的正方形的对角线的长是多少？
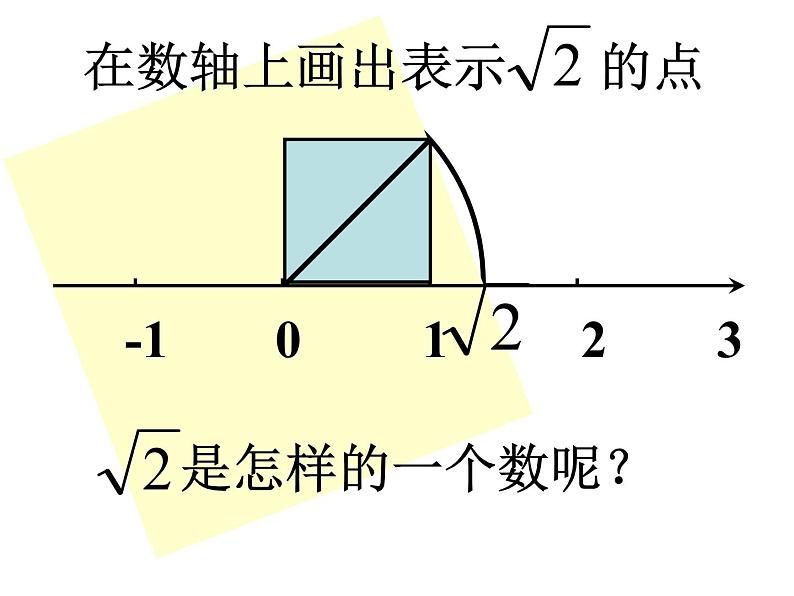
是怎样的一个数呢？
在数轴上画出表示 的点
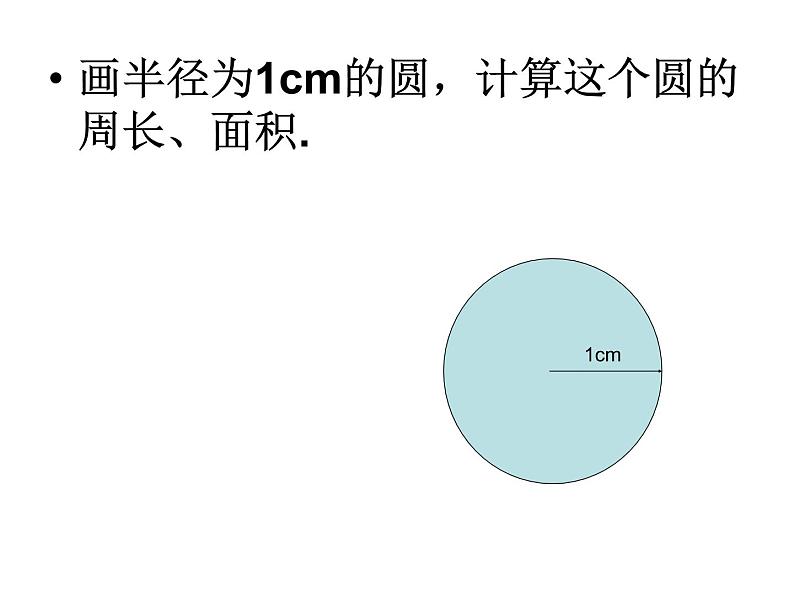
画半径为1cm的圆，计算这个圆的周长、面积.
事实上，人们已经证明 是一个无限不循环小数，它的值为 1.414 213 562 373 095 048 801 688 724 209 7…
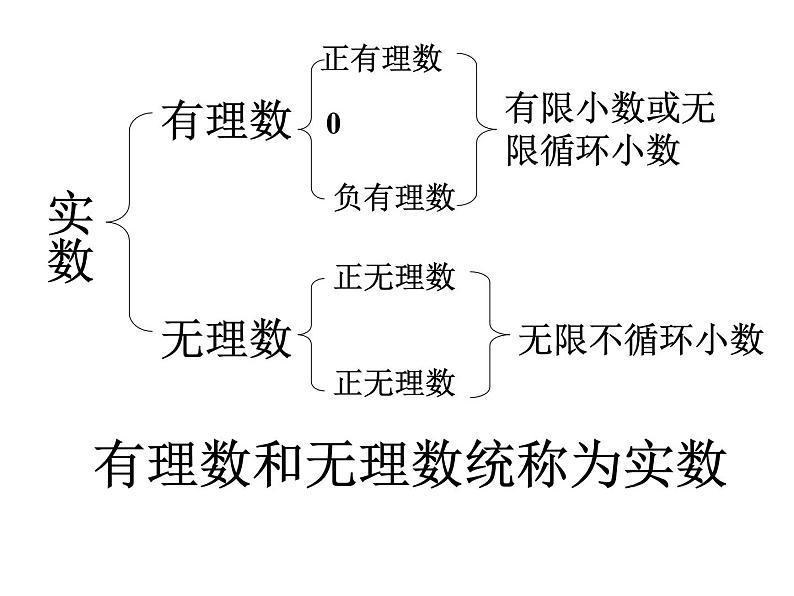
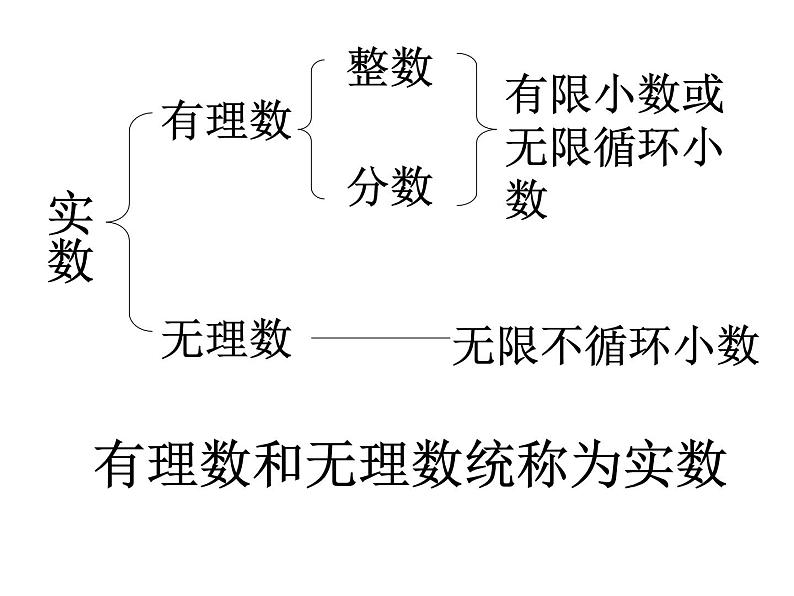
无限不循环小数称为无理数。
有限小数或无限循环小数
有理数和无理数统称为实数
有理数都可以用数轴上的点来表示，反过来，数轴上的点是否都表示有理数？
有理数集合{ …} 无理数集合{ …}正实数集合{ …}负实数集合{ …}
例1、把下列各数填入相应的集合内：
0.12121121112…
2500多年前，古希腊有一位伟大的数学家——毕达哥拉斯。他最伟大的贡献就是发现了“勾股定理”。所以直到现在，西方人仍然称勾股定理为“毕达哥拉斯定理”。据传说，当勾股定理被发现之后，毕达哥拉斯学派的成员们曾经杀了99头牛来大摆筵席，以示庆贺。 其后不久，他的弟子希勃索斯(Hippasus)通过勾股定理，发现了一个惊人的事实，边长为1的正方形的对角线长度并不是有理数。这下可惹祸了，因为毕达哥拉斯一向认为“万物兼数”，而他所说的“数”，仅仅是整数与整数之比，也就是现代意义上的“有理数”（整数和分数的统称）。也就是说，他认为除了有理数以外，不可能存在另类的数。
当希勃索斯提出他的发现之后，毕达哥拉斯大吃一惊，原来世界上真的有“另类数”存在。 15世纪意大利著名画家达.芬奇称之为“无理的数”，17世纪德国天文学家开普勒称之为“不可名状”的数。这一发现使该学派领导人惶恐、恼怒，认为这将动摇他们在学术界的统治地位。希勃索斯因此被囚禁，受到百般折磨，最后竞遭到沉舟身亡的惩处。 希勃索斯终于为宣传科学而献出了宝贵的生命，这在科学史上留下了悲壮的一页。正因为希勃索斯发现了无理数，数的概念才得以扩充。从此，数学的研究范围扩展到了实数领域。
1、比较大小：
3、比较大小： 3
1. a是一个实数,它的相反数为____；
如果，a≠0那么它的倒数为______.
6.设m是 的整数部分，n是 的小数部分， 试求 n（ +m ）的值