初中数学人教版八年级上册14.1.2 幂的乘方优秀ppt课件

这是一份初中数学人教版八年级上册14.1.2 幂的乘方优秀ppt课件，文件包含1412-1413幂的乘方与积的乘方课件pptx、1412-1413幂的乘方与积的乘方教案doc、1412-1413幂的乘方与积的乘方练习doc等3份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

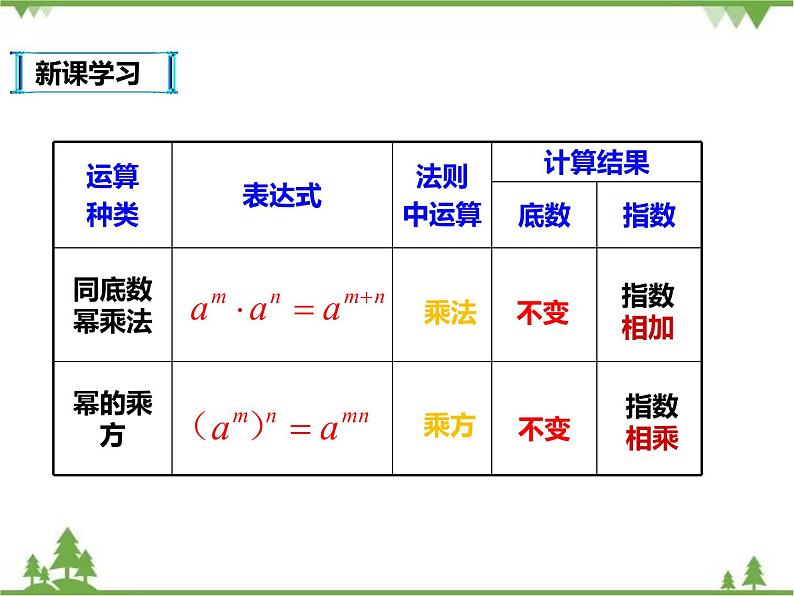
法则：同底数的幂相乘，底数不变，指数相加。
（其中m、n为正整数）
如 am·an·ap =
根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:(1)（32）3 = 32×32×32 = 3( ) (2)（a2）3 = a2 × a2 × a2 =a( ) (3)（am）3 =am × am × am= a ( ) (m是正整数)
对于任意底数a与任意正整数m,n,(am)n=?
(同底数幂的乘法法则)
（m，n都是正整数）．
幂的乘方，底数 ，指数 ．
例1:计算:(103)5 ; (2) (a4)4 ; (3) (am)2 ; (4) -(x4)3 。
解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16; (3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .
1、已知ax=3,ay=2,试求a2x+3y的值。
分析：首先根据同底数幂的乘法法则，可得a2x+3y=a2x×a3y，然后根据幂的乘方的运算方法，可得a2x×a3y=(ax)2 ×(ay)3，最后把ax=3,ay=2代入化简后的算式，求出值是多少即可。
解：∵ax=3,ay=2, ∴ a2x+3y=a2x×a3y=(ax)2 ×(ay)3=32×23=72
2、已知2m=a,32n=b,试求23m+10n的值。
分析：首先根据同底数幂的乘法法则，可得23m+10n=23m×210n=(2m)3×(25n)2 ，然后根据2m=a,32n=b,求出值即可。
解：∵2m=a,32n= (25n)2 = b, ∴ 23m+10n=23m×210n=(2m)3×(25n)2 =a3b2
1.判断题(1) (x3)2=x3+2=x5 ( )(2) a ×(-a2)3=a7 ( )(3) (xm-3)3=x3m-9 ( )
2.设n为正整数，且x2n=3，求（x3n）2-4（x3）2n的值．
解：∵x2n=3，∴（x3n）2-4（x3）2n=（x2n）3-4（x2n）3=27-4×27=-81．
①(ab)2=(ab)·(ab)=(a·a)(b·b)=a（ ）b（ ）；②(ab)3＝_ ____＝ ___ __ ＝a（ ）b（ ）；③(ab)4＝ _ ____ ＝ _ ____ ＝a（ ）b（ ）.猜想：(ab)n＝a（ ）b（ ）
(ab)·(ab) ·(ab)
(a·a·a) (b·b·b)
(ab)·(ab) ·(ab) ·(ab)
(a·a·a·a) (b·b·b·b)
把积的每一个因式分别乘方，再把所得的幂相乘。
因此可得：(ab)n=anbn (n为正整数)
(abc)n=an·bn·cn
(2a)3; (2) (-5b)3(3) (xy2)2; (4) (-2x3)4
解: (1)(2a)3=23·a3=8a3;(2) (-5b)3=(-5)3·b3=-125b3;(3) (xy2)2=x2·(y2)2=x2y4;(4) (-2x3)4=(-2)4·(x3)4=16x12
例题3：计算：①（－2a2b3c）3； ②［－a2·（－a4b3）3］3.
运用积的乘方法则计算时，注意每个因式都要乘方，尤其是字母的系数不要漏乘方.
①原式＝（-2）3·（a2）3·（b3）3·c3
②原式＝（－1）3·（a2）3·（－a4b3）9
＝（－1）·a6·（－1）9（a4）9（b3）9
(1)原式＝(4 × 0.25)8=(1)8=1
灵活变化，使可以用乘法法则。
2、如果3n•27n•81n=916，求n的值
分析：把3n•27n•81n化为94n求解即可．
解：∵3n•27n•81n=916，∴94n=916，∴4n=16，解得n=4．
2(x3)2 · x3－(3x3)3＋(5x)2 ·x7
解：原式=2x6 · x3－27x9+25x2 ·x7
注意：运算顺序是先乘方，再乘除，最后算加减
=2x9－27x9+25x9
3.已知10m=5，10n=2，求102m+3n的值．
解析：首先根据同底数幂的乘法法则，可得102m+3n=102m×103n，然后根据幂的乘方的运算方法，可得102m×103n=（10m）2×（10n）3，最后把10m=5，10n=2代入化简后的算式，求出102m+3n的值是多少即可．
解析：∵10m=5，10n=2，∴102m+3n=102m×103n=（10m）2×（10n）3=52×23=25×8=200．
灵活运用乘法法则的逆用。
(am)n=amn（m、n为正整数）
(ab)n=anbn (n为正整数)
1. 若a=355,b=444,c=533,比较a、b、c的大小
分析：先把a、b、c、都变为相同幂的形式，然后进行比较底数的大小，从而可以比较大小。
2. （1）已知：2x+5y-3=0，求4x•32y的值；（2）若n为正整数，且x2n=7，求（-2xn）4+（3x3n）2．
解析：（1）逆用幂的乘方的性质先写成以2为底的幂相乘，再逆用同底数幂的乘法的性质计算，然后把已知条件代入计算即可；（2）根据幂的乘方的性质，将式子进行变形然后代入数据计算即可
解析：（1）4x•32y=22x•25y=22x+5y，∵2x+5y-4=0，∴2x+5y=4，∴原式=24=16．
（2）∵x2n=7，∴（-2xn）4+（3x3n）2，=16（x2n）2+9（x2n）3=16×72+9×73=784+3087=3871