人教版八年级上册14.3 因式分解综合与测试优秀课件ppt

这是一份人教版八年级上册14.3 因式分解综合与测试优秀课件ppt，共15页。PPT课件主要包含了什么叫因式分解，知识点回顾，因式分解的步骤，如何找公因式，基本题型练习一，试一试，基本题型练习二，十拓展题等内容，欢迎下载使用。

把一个多项式写成几个整式的乘积的形式，叫做把这个多项式分解因式．
例 下列变形是否是因式分解.
1、要分解到不能再分为止，括号内合并同类项后注意把数字因数提出来。
2、因式分解的结果是连乘式。
3、因式分解的结果里没有中括号。
（1）取各项系数的最大公约数；（2）取各项都含有的相同字母；（3）取相同字母的最低次幂．
二、因式分解的基本方法一:提取公因式法
2. 提取公因式时要注意什么?
例: 下列用提取公因式法分解因式是否正确?
1 熟记公式及其特点（1）平方差公式,:a2-b2=(a+b)(a-b)（2）完全平方公式: a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
三、因式分解的基本方法二:运用公式法
例 下列多项式哪些能用乘法公式分解因式
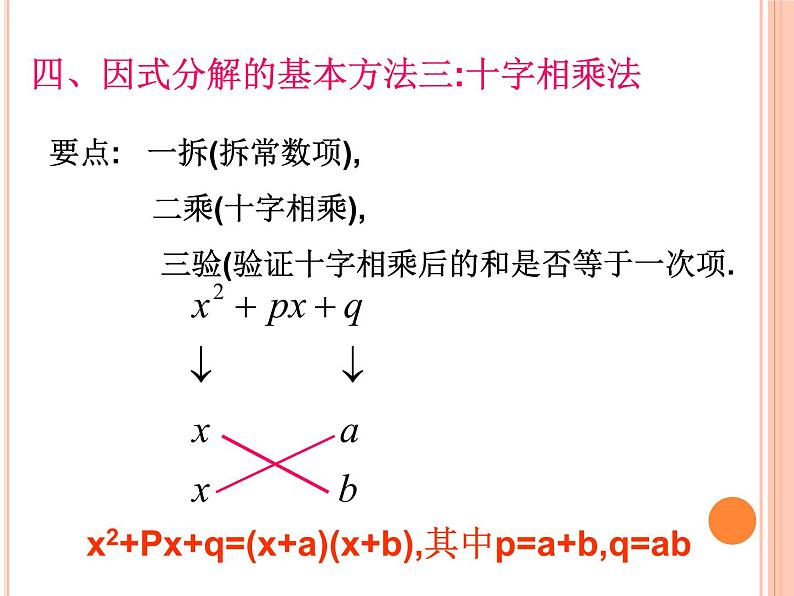
x2+Px+q=(x+a)(x+b),其中p=a+b,q=ab
四、因式分解的基本方法三:十字相乘法
要点: 一拆(拆常数项), 二乘(十字相乘), 三验(验证十字相乘后的和是否等于一次项.
五、因式分解的基本方法四:分组分解法
要点:先观察特征,后正确分组,注意加括号.
2 注意点: 在分解因式时要注意各个因式是否还能继续分解， 直到每一个因式都不能继续分解为止.
六: 一般步骤与注意点
1 一般步骤: 先提公因式,再运用公式或十字相乘,后分组分解,最后是重新整理再分解.
(2) 若4a2＋ma＋9是一个完全平方式，则m＝___
(1) 若9a2b2＋12ab＋_____=( + )2
(3) 若x2＋3x－4=(x＋a)(x＋b),则
(4) 若2a-b=0，则
九、因式分解的简单应用
若在多项式x2+1中加上一个单项式后正好是一个完全平方式，则这个单项式可以是＿＿＿＿＿＿＿＿＿＿＿＿（写出所有可能）．
设2n,2n-2是两个连续偶数，利用因式分解证明：两个连续偶数的平方差是4的倍数。
证明:对于任意正整数n, 都是10的倍数.
2) 求满足 的整数解x和y .