人教版七年级下册5.2.2 平行线的判定授课ppt课件

这是一份人教版七年级下册5.2.2 平行线的判定授课ppt课件，共16页。PPT课件主要包含了考考你，练一练，简说为，∠1∠2，AB∥CD，a∥b，答AB∥CD，理由如下，角平分线定义，等量代换等内容，欢迎下载使用。

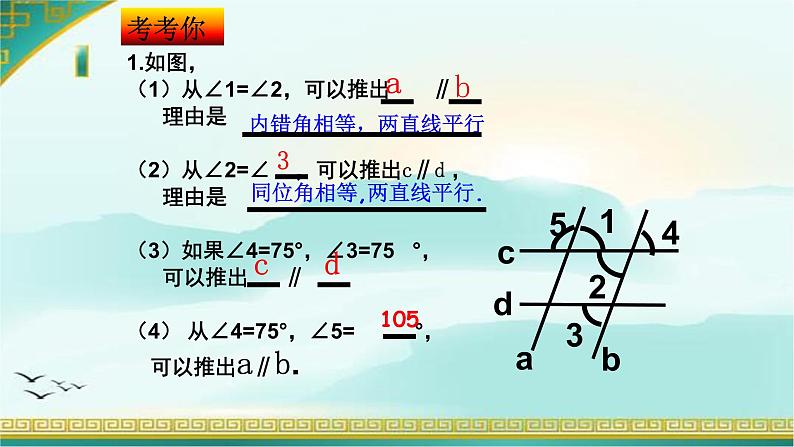
1.如图，（1）从∠1=∠2，可以推出 ∥ 理由是（2）从∠2=∠ ，可以推出c∥d ， 理由是（3）如果∠4=75°，∠3=75 °， 可以推出 ∥ （4） 从∠4=75°，∠5= °， 可以推出a∥b.
内错角相等，两直线平行
同位角相等,两直线平行.
从∠1=∠4，可以推出　 ∥ ， 理由是 。
(3)从∠ABC +∠ =180，可以推出AB∥CD ， 理由是 。
(2)从∠2=∠ ，可以推出AD∥BC， 理由是 。
(4)从∠5=∠ ，可以推出AB∥CD， 理由是 。
同旁内角互补,两直线平行
同位角相等,两直线平行
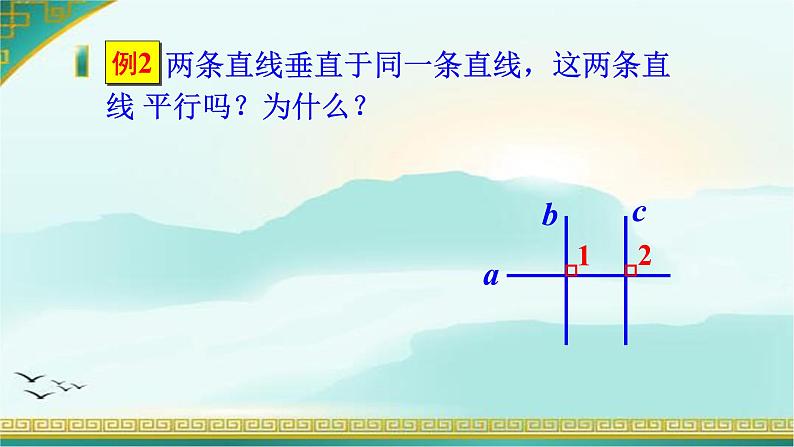
两条直线垂直于同一条直线，这两条直线 平行吗？为什么？
如果两条直线都垂直于同一条直线，那么这两条直线平行。
垂直于同一条直线的两条直线平行.
1.同位角相等, 两直线平行.2.内错角相等, 两直线平行.3.同旁内角互补, 两直线平行.4.如果两条直线都与第三条直线平行， 那么这两条直线也互相平行.5.在同一平面内,如果两条直线都垂直于 同一条直线，那么这两条直线平行。
判定两条直线是否平行的方法有：
如图：直线AB、CD都和AE相交，且∠1+∠A=180º ．求证：AB//CD
证明：∵∠1+∠A=180º
∴∠2+∠A=180º
( ）
（ ）
( ）
同旁内角互补，两直线平行
（1）如图1，∠C＝57°， 当∠ABE＝ °时，就能使BE∥CD.
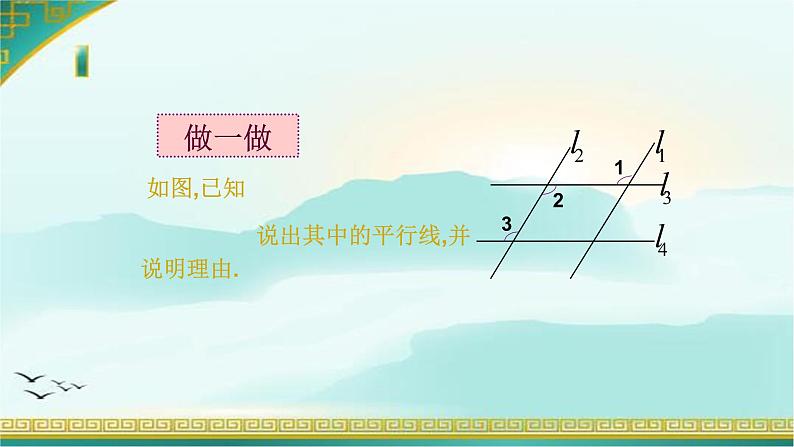
（2）如图2 ， ∠1＝120°,∠2＝60°． 问a与b的关系？
例1：已知：如图，ABC、CDE都是直线， 且∠1=∠2，∠1=∠C，求证：AC∥FD.
∵ ∠1 = ∠2， ∠1 = ∠C （已知）
∴ ∠2=∠C （等量代换）
∴ AC∥FD （同位角相等，两直线平行）
例3：如图，已知∠1= ∠3，AC平分∠DAB你 能判断那两条直线平行？请说明理由？

∵ AC平分∠DAB（ ）
∴ ∠1=∠2（ ）
又∵ ∠1= ∠3（ ）
∴ ∠2=∠3（ ）
∴ AB∥CD( )
∵ ∠1=∠C （已知）
∴ MN∥BC （内错角相等，两直线平行）
∵ ∠2=∠B （已知）
∴ EF∥BC （同位角相等，两直线平行）
∴ MN∥EF （ ）
练习3：已知：如图，∠1=∠C，∠2=∠B， 求证：MN∥EF.
平行于同一直线的两条直线平行
（1）∵∠1 =∠4（已知）∴____∥____( )（2）∵∠___= ∠___(已知）∴BC ∥ EF( ) (3) ∵∠1= ∠___(已知）∴DE ∥____( )
（A）∠2＝∠3 （B）∠1＝∠4 （C）∠1＝∠2 （D）∠1＝∠3