









数学七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定评优课教学ppt课件
展开1.掌握平行线的三种判定方法,会运用判定方法来判断两条直线是否平行;(重点)
2.能够根据平行线的判定方法进行简单的推理.
在同一个平面内,不相交的两条直线叫做平行线.记作a∥b.
2.基本事实(平行公理):
也就是说:如果b∥a,c∥a,那么b∥c.几何语言:∵ b∥a,c∥a,∴ b∥c.
经过直线外一点,有且只有一条直线与这条直线平行.
如果两条直线都与第三条直线平行,那么这两条直线也
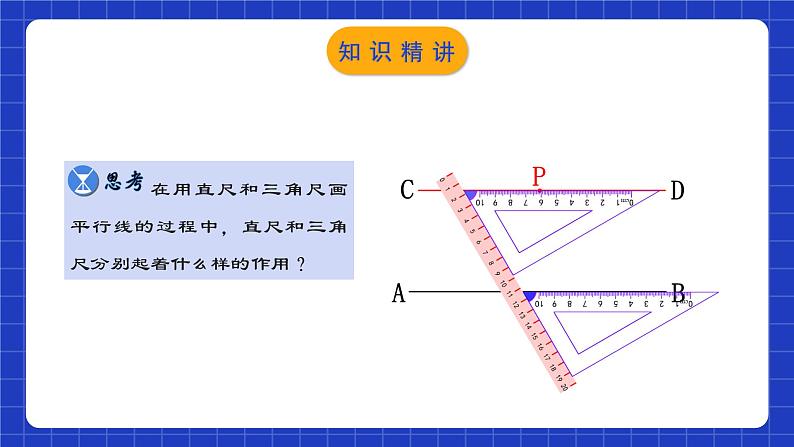
如何用直尺和三角板过直线AB外一点P做AB的平行线CD.
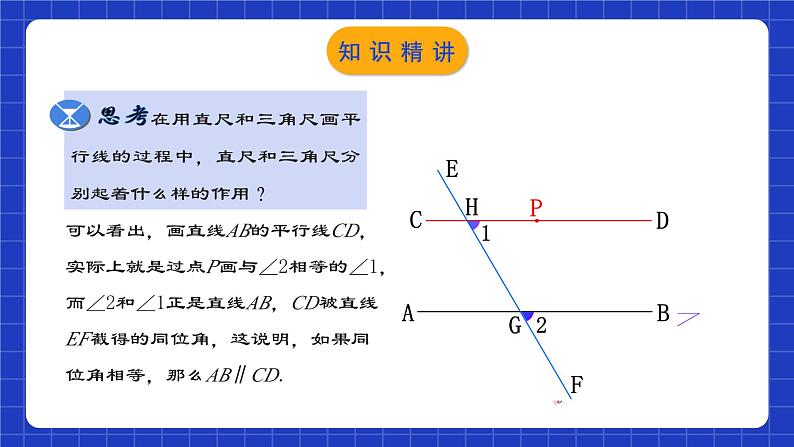
在用直尺和三角尺画平行线的过程中,直尺和三角尺分别起着什么样的作用?
可以看出,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角,这说明,如果同位角相等,那么AB∥CD.
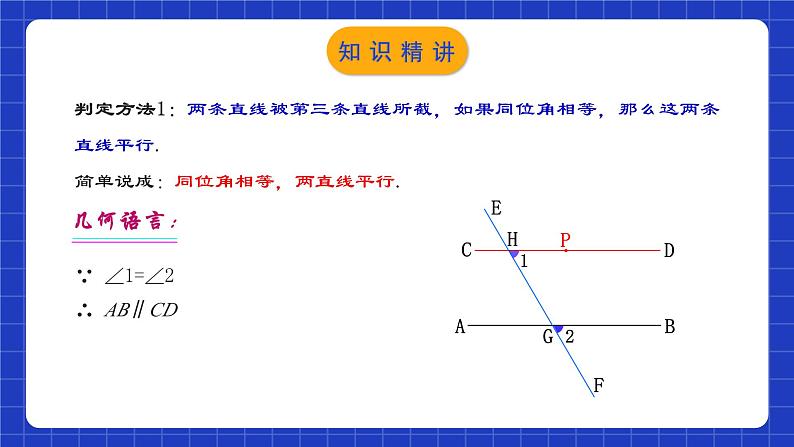
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.
∵ ∠1=∠2∴ AB∥CD
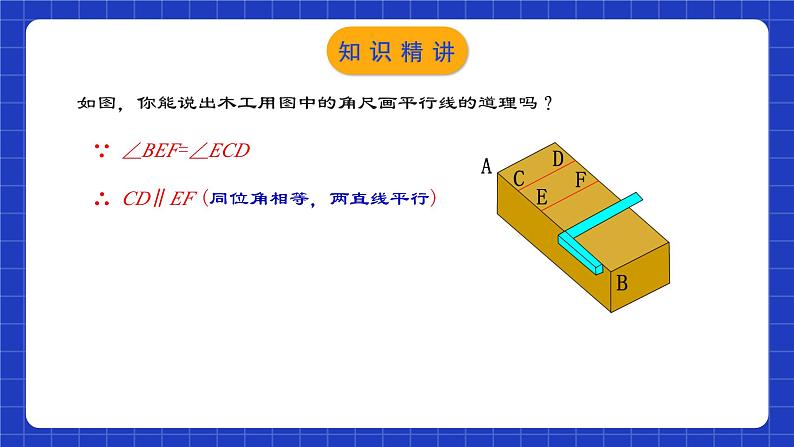
如图,你能说出木工用图中的角尺画平行线的道理吗?
∵ ∠BEF=∠ECD∴ CD∥EF (同位角相等,两直线平行)
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角. 由同位角相等,可以判定两条直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?
(1) 内错角满足什么关系时?两直线会平行?(2) 同旁内角满足什么关系时?两直线会平行?
如图,由3=2,可推出a∥b吗?
解: a∥b .∵ 3=2(已知) 1=3(对顶角相等)∴ 1=2(等量代换)∴ a∥b (同位角相等,两直线平行)
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 简单说成:内错角相等,两直线平行.
如图,由2+4=180°,可推出a∥b吗?
解: a∥b .∵ 2+4=180° (已知) 1+4=180°(邻补角定义)∴ 1=2(同角的补角相等)∴ a∥b (同位角相等,两直线平行)
解: a∥b .∵ 2+4=180° (已知) 3+4=180°(邻补角定义)∴ 2=3(同角的补角相等)∴ a∥b (内错角相等,两直线平行)
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.
∵ ∠1+∠2=180°∴ AB∥CD
遇到一个新问题时,常常把它转化为已知的(或已经解决的)问题来解决.这一节中,我们利用“同位角相等,两直线平行”得到了“内错角相等,两直线平行”和“同旁内角互补,两直线平行”. 因此,在解题的过程中,可以用这种思路去分析实际问题,从而解决问题.
同位角相等,两直线平行.内错角相等,两直线平行. 同旁内角互补,两直线平行.
例1.如图,AB⊥EF于点B,CD⊥EF于点D,∠1=∠2,试判断BM与DN是否平行,为什么?
已知:如图,CF平分∠ACM,∠1=72°,∠2=36°,判断CM与DN是否平行,并说明理由.
解:CM∥DN ∵CF平分∠ACM∴∠ACM=2∠1∵∠1=72°∴∠ACM=2∠1=144°∴∠BCM=180°-144°=36°∵∠2=36°,∴∠2 =∠BCM.∴CM∥DN
内错角相等,两直线平行
1.如图所示,直线a,b被c所截,现给出下列四个条件:①∠1=∠5;②∠3+∠6=180°;③∠2+∠3=180°;④∠4=∠5.其中能判定a//b的条件有序号是( )A.①② B.①③ C.①④ D.③④2.如图,下列条件中,能判断直线.l1//l2的是( )A.∠2=∠3 B.∠1=∠3 C.∠4+∠5=180° D.∠2=∠4
3.如图,下列条件中,能判断直线l1//l2的是( )A.∠1=∠2 B.∠1=∠5C.∠1+∠3=180° D.∠3=∠54.如图,下列结论中正确的是( ) A.若∠1=∠4,则m//cB.若∠1=∠2,则a//bC.若∠1+∠3=180,则n//cD.若∠2+∠3=180°,则m//n
5.如图(1),光线AB,CD被一个平面镜反射,此时∠1=∠3,∠2=∠4,则AB // _____,BE_____DF.6.如图(2),已知∠C=100°,若增加一个条件,使得AB // CD,试写出符合要求的一个条件:___________________.
7.如图,∠B=∠3,则____//_____,根据的是__________________________;若∠2=∠A,则____//_____,根据的是_______________________________;若∠2=∠E,则____//_____,根据的是_______________________________;若∠B+∠BCE=180°,则____//_____,根据的是________________________________.
同位角相等,两直线平行
同旁内角互补,两直线平行
8.如图,BE是AB的延长线. (1)由∠CBE=∠A可以判定哪两条直线平行?根据什么? (2)由∠CBE=∠C可以判定哪两条直线平行?根据什么?
解:(1)∵ ∠CBE=∠A∴ AD∥BC(同位角相等,两直线平行)(2)∵ ∠CBE=∠C∴ CD∥AE(内错角相等,两直线平行)
9.如图,∠1=∠2=55°,∠3等于多少度?直线AB、CD平行吗?说明你的理由.
解: ∠3=55°,AB//CD.∵ ∠l=∠2=55°(已知) ∠2=∠3 (对顶角相等)∴ ∠3=∠1=55°(等量代换)∴ AB//CD (同位角相等,两直线平行)
10.如图,已知∠B=60°,∠ADE是∠B的2倍,那么直线EF与BC平行吗?请说明理由.
解: EF//BC.∵ ∠B=60° (已知)∴ ∠ADE=2∠B=120° (已知)∴ ∠BDF=∠ADE=120° (对顶角相等)∴ ∠B+∠BDF=180° (等式的性质)∴ EF//BC (同旁内角互补,两直线平行)
11.小明有一块小画板,他想知道它的上、下边缘是否平行,而小明身边只有一个量角器,你能帮他解决这一问题吗?
解:在上、下边缘之间画一条线段AB(如图所示),得到四个角.利用量角器测量出∠1和∠4(或∠1和∠3或∠2和∠3或∠2和∠4)中的一组角的度数.然后利用内错角相等,两直线平行或同旁内角互补,两直线平行来判定上、下边缘是否平行.
判定方法1:同位角相等,两直线平行.判定方法2:内错角相等,两直线平行. 判定方法3:同旁内角互补,两直线平行.
判定两条直线平行的方法:
数学10.2 直方图精品教学课件ppt: 这是一份数学<a href="/sx/tb_c42631_t3/?tag_id=26" target="_blank">10.2 直方图精品教学课件ppt</a>,文件包含人教版数学七年级下册1022《直方图2》课件pptx、人教版数学七年级下册1022《直方图2》教学设计docx、人教版数学七年级下册1022《直方图2》导学案docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学人教版七年级下册第十章 数据的收集、整理与描述10.2 直方图获奖教学课件ppt: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c42631_t3/?tag_id=26" target="_blank">第十章 数据的收集、整理与描述10.2 直方图获奖教学课件ppt</a>,文件包含人教版数学七年级下册1021《直方图1》课件pptx、人教版数学七年级下册1021《直方图1》教学设计docx、人教版数学七年级下册1021《直方图1》导学案docx等3份课件配套教学资源,其中PPT共37页, 欢迎下载使用。
人教版七年级下册10.1 统计调查精品教学ppt课件: 这是一份人教版七年级下册<a href="/sx/tb_c42629_t3/?tag_id=26" target="_blank">10.1 统计调查精品教学ppt课件</a>,文件包含人教版数学七年级下册1011《全面调查》课件pptx、人教版数学七年级下册1011《全面调查》教学设计docx、人教版数学七年级下册1011《全面调查》导学案docx等3份课件配套教学资源,其中PPT共36页, 欢迎下载使用。














