初中数学人教版八年级下册18.2.1 矩形优秀课件ppt

这是一份初中数学人教版八年级下册18.2.1 矩形优秀课件ppt，共29页。PPT课件主要包含了素养目标，矩形的判定定理1，∴ABDC，几何语言，又∵OAOD，∴ACBD，∴∠BAD90°，∴∠OAB40°，利用对角线判定矩形，矩形的判定定理2等内容，欢迎下载使用。

一位很有名望的木工师傅，招收了两名徒弟，一天，师傅有事外出，两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门，做完之后，两人都说对方的门不是矩形，而自已的是矩形. 你能想一个办法确定谁做的门是矩形吗？
2. 能应用矩形定义、判定等知识，解决简单的证明题和计算题.
1. 理解并掌握矩形的判定方法 .
3.提高学生合情推理和演绎推理的能力.
小明利用周末的时间，为自己做了一个相框．
问题1 请你利用直尺和三角板帮他检验一下，相框是矩形吗？　　除了矩形的定义外，有没有其他判定矩形的方法呢？
问题2 你还记得学习平行四边形的判定时，我们是如何猜想并进行证明的吗？
同样，小明通过研究矩形性质的逆命题，得到判定矩形的方法呢？ 　　小明的猜想:　对角线相等的四边形是矩形．　　　　
问题3 上节课我们已经知道“矩形的对角线相等”，反过来，小明猜想对角线相等的四边形是矩形，你觉得对吗？
【讨论】你能证明这一猜想吗？
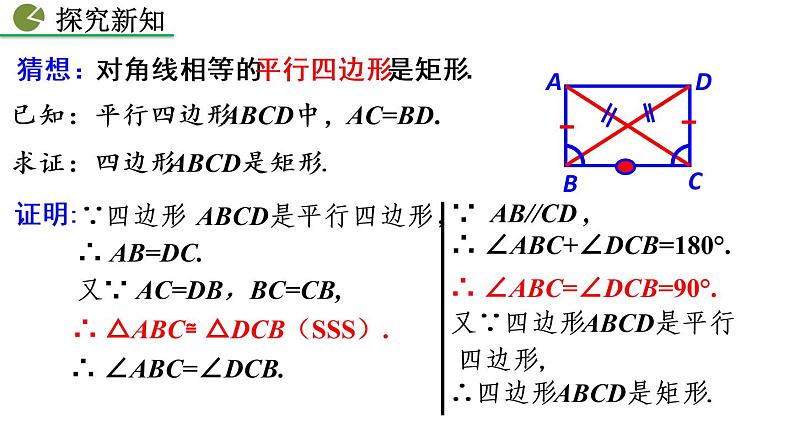
猜想：对角线相等的平行四边形是矩形.
已知：平行四边形ABCD中，AC=BD.求证：四边形ABCD是矩形.
∴ △ABC≌ △DCB（SSS）.
∵ AB//CD ,∴ ∠ABC+∠DCB=180°.
∴ ∠ABC=∠DCB=90°. 又∵四边形ABCD是平行 四边形,
∴四边形ABCD是矩形.
∴ ∠ABC=∠DCB.
∵四边形 ABCD是平行四边形，
又∵ AC=DB，BC=CB,
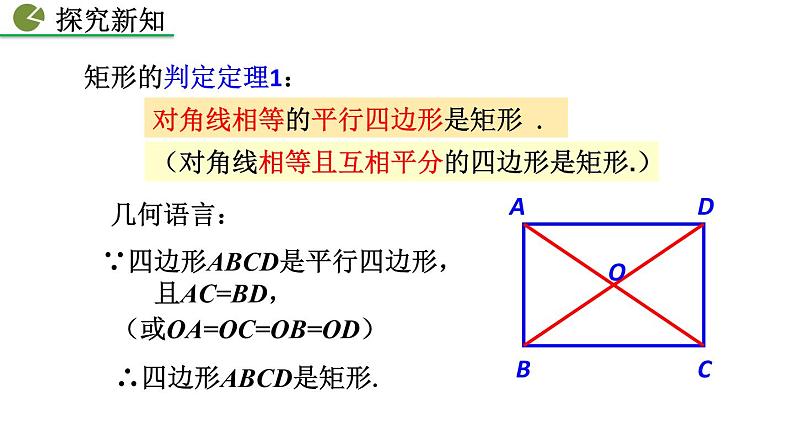
对角线相等的平行四边形是矩形 .
∵四边形ABCD是平行四边形， 且AC=BD，
（对角线相等且互相平分的四边形是矩形.）
（或OA=OC=OB=OD）
解：∵四边形ABCD是平行四边形，
又∵∠OAD=50°，
解：四边形ABCD是矩形.理由如下：∵四边形ABCD是平行四边形,∴ AO=CO,DO=BO.又∵∠1= ∠2，∴AO=BO.∴AC=BD.∴四边形ABCD是矩形.
问题1 前边我们学习了矩形的四个角，知道它们都是直角，它的逆命题是什么？成立吗？
逆命题：四个角是直角的四边形是矩形.
问题2 四边形至少有几个角是直角就是矩形呢？
做一做 李芳同学由“边——直角、边——直角、边——直角、边”这样四步，画出了一个四边形，她说这就是一个矩形，她的判断对吗？为什么？
猜想：有三个角是直角的四边形是矩形 .
已知：如图,在四边形ABCD中,∠A=∠B=∠C=90°.求证：四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°，∴AD∥BC , AB∥CD.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
∵ ∠A=∠B=∠C=90° ∴四边形ABCD是矩形.

有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形 .
例 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
证明：∵CF平分∠ACD， ∴∠1=∠2. 又∵ MN∥BC， ∴∠1=∠3. ∴ ∠2=∠3. 同理可证：OC=OE. ∴OE=OF.
(2)当O运动到何处时, 四边形AECF为矩形?
利用角判断四边形是矩形
答：当点O为AC的中点时，四边形AECF是矩形.理由：由（1）知OE=OF, 又AO=CO, ∴四边形AECF是平行四边形. 又∵EC, FC分别平分∠ACB ,∠ACD, ∴∠2+∠4=90°,即∠ECF=90°. ∴四边形 AECF是矩形.
如图， □ ABCD的四个内角的平分线分别相交于E，F，G，H，求证：四边形 EFGH为矩形．
证明：在□ ABCD中，AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB,∠ABC的平分线,
∴四边形EFGH是矩形．
同理可证∠AED=∠EHG=90°,
1. 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（　　）A．∠A=∠B B．∠A=∠CC．AC=BD D． AB⊥BC
2. 已知：如图，在▱ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．（1）求证：△ABE≌△CDF.（2）求证：四边形AECF是矩形．
（1）证明：∵四边形ABCD是平行四边形，∴∠B＝∠D，AB＝CD，AD∥BC.∴∠AEB＝∠AEC＝∠CFD＝∠AFC＝90°.在△ABE和△CDF中， ∴△ABE≌△CDF（AAS）.（2）证明：∵AD∥BC，∴∠EAF＝∠AEC＝∠AFC＝90°.
∴四边形AECF是矩形．
∴∠EAF＝∠AEB＝90°.
∵AE⊥BC，CF⊥AD，
1.如图，在▱ABCD中，AC和BD相交于点O，则下面条件能判定▱ABCD是矩形的是 （　　）
A．AC=BD B．AC=BCC．AD=BC D．AB=AD
2.如图,直线EF∥MN , PQ交EF , MN于A , C两点,AB , CB , CD , AD分别是∠EAC , ∠MCA , ∠ ACN , ∠CAF的平分线,则四边形ABCD是 （ ）A.梯形 B.平行四边形 C.矩形 D.不能确定
3.如图,矩形ABCD的对角线AC , BD相交于点O，E ， F ， G ， H分别是AO ， BO ， CO ， DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
∵四边形ABCD是矩形，
AO=BO=CO=DO.
∵ AE=BF=CG=DH，
∴OE=OF=OG=OH.
∴四边形EFGH是平行四边形.
∵EO+OG=FO+OH，即EG=FH，
∴四边形EFGH是矩形.
4.如图，在四边形ABCD中，AB∥CD，∠BAD=90°，AB=5，BC=12，AC=13．求证：四边形ABCD是矩形．
证明：四边形ABCD中，AB∥CD，∠BAD=90°，∴∠ADC=90°.又∵△ABC中，AB=5，BC=12，AC=13，满足132=52+122，即∴△ABC是直角三角形，且∠B=90°.∴四边形ABCD是矩形．
如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E，求证：四边形ADCE为矩形．
证明：在△ABC中，AB＝AC，AD⊥BC， ∴∠BAD＝∠DAC，即∠DAC＝ ∠BAC.又∵AN是△ABC外角∠CAM的平分线，∴∠MAE＝∠CAE＝ ∠CAM,∴∠DAE＝∠DAC＋∠CAE＝ (∠BAC＋∠CAM)＝90°.又∵AD⊥BC，CE⊥AN，∴∠ADC＝∠CEA＝90°,∴四边形ADCE为矩形．
如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝24cm，BC＝26cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P，Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．(1)经过多长时间，四边形PQCD是平行四边形？
解：设经过xs，四边形PQCD为平行四边形， 即PD＝CQ， 所以24－x＝3x， 解得x＝6. 即经过6s，四边形PQCD是平行四边形.
(2)经过多长时间，四边形PQBA是矩形？
解：设经过ys，四边形PQBA为矩形，即AP＝BQ，∴y＝26－3y，解得y＝6.5，即经过6.5s，四边形PQBA是矩形.
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明