人教版八年级下册18.2.2 菱形公开课ppt课件

这是一份人教版八年级下册18.2.2 菱形公开课ppt课件，共27页。PPT课件主要包含了对角线，菱形的四条边相等，菱形的邻角互补，菱形的性质，素养目标，数学语言，菱形的判定定理1，∴OAOC，又∵AC⊥BD，∴BABC等内容，欢迎下载使用。

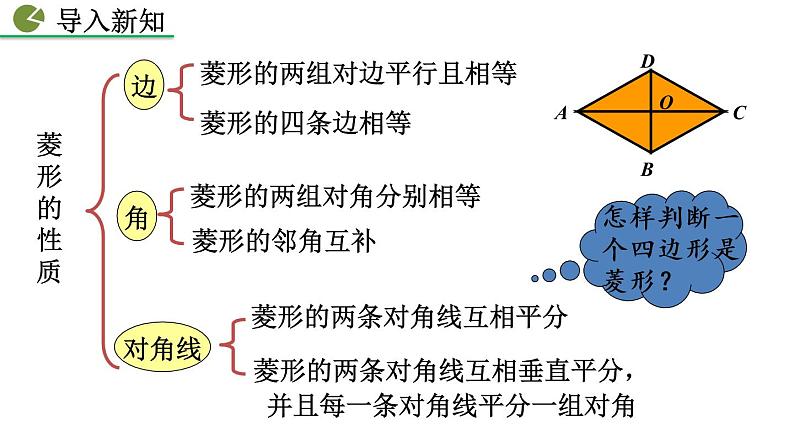
菱形的两条对角线互相平分
菱形的两组对边平行且相等
菱形的两组对角分别相等
菱形的两条对角线互相垂直平分，并且每一条对角线平分一组对角
2. 经历菱形判定定理的探究过程，渗透类比思想，体会研究图形判定的一般思路.
1. 掌握菱形的三种判定方法，能根据不同的已知条件，选择适当的判定定理进行推理和计算 .
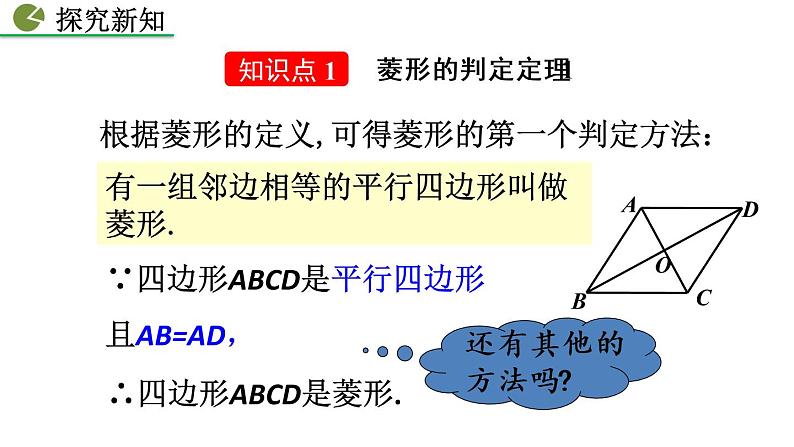
根据菱形的定义,可得菱形的第一个判定方法：
∵四边形ABCD是平行四边形且AB=AD，
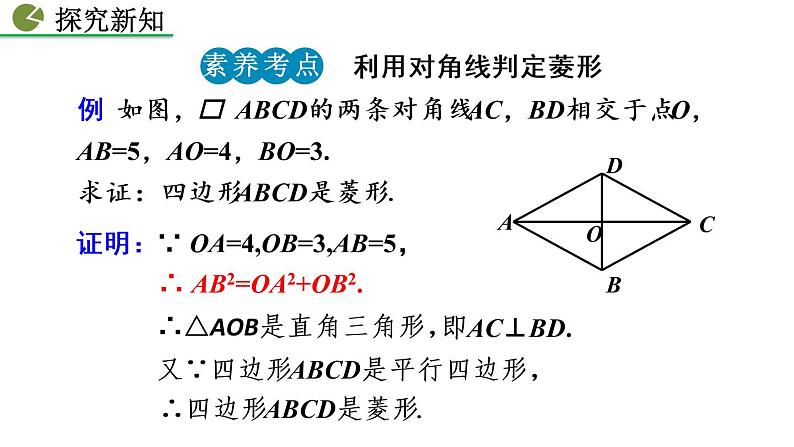
∴四边形ABCD是菱形.
有一组邻边相等的平行四边形叫做菱形.
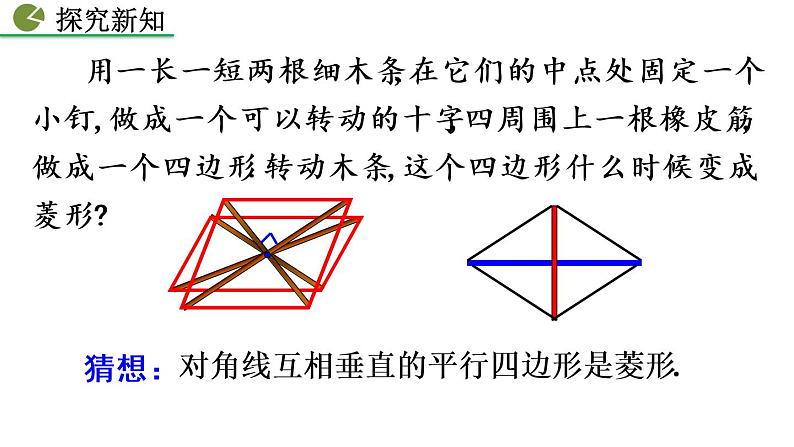
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
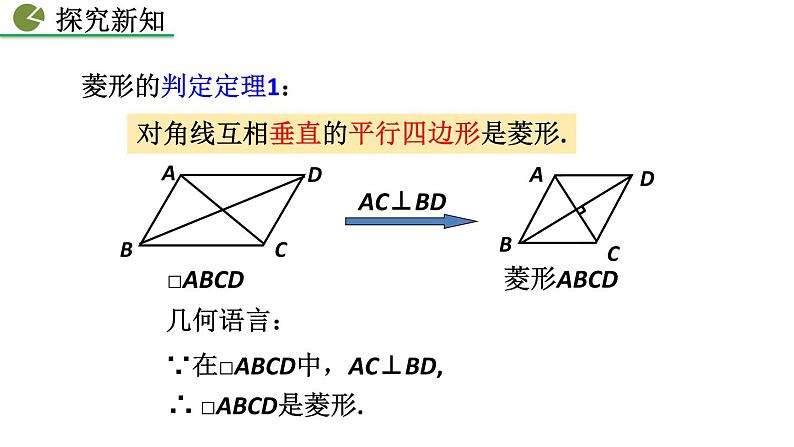
对角线互相垂直的平行四边形是菱形.
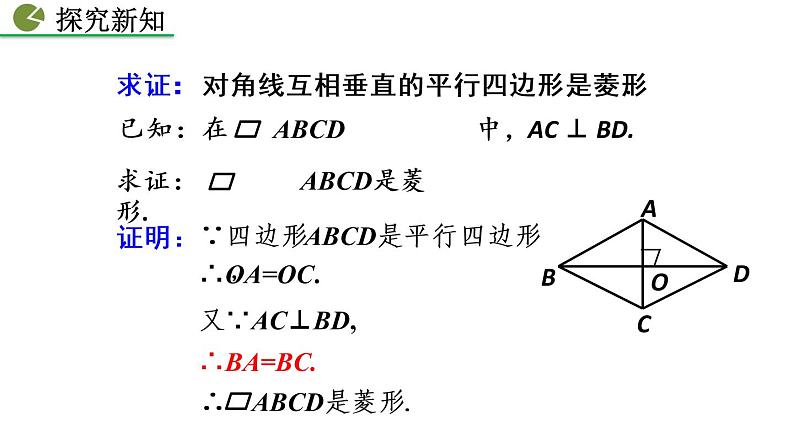
求证：对角线互相垂直的平行四边形是菱形.
∵四边形ABCD是平行四边形,
几何语言：∵在□ABCD中，AC⊥BD,
∴ □ABCD是菱形.
又∵四边形ABCD是平行四边形，
∵ OA=4,OB=3,AB=5，
∴ AB2=OA2+OB2.
∴△AOB是直角三角形，
在四边形ABCD中，对角线AC，BD互相平分，若添加一个条件使得四边形ABCD是菱形，则这个条件可以是 （ 　 ）A．∠ABC=90° B．AC⊥BDC．AB=CD D．AB∥CD
猜想：四条边都相等的四边形是菱形 .
李芳同学先画两条等长的线段AB , AD，然后分别以B，D为圆心，AB为半径画弧，得到两弧的交点C，连接BC，CD，就得到了一个四边形，猜一猜，这是什么四边形？
证明：∵AB=BC=CD=AD, ∴AB=CD , BC=AD. ∴四边形ABCD是平行四边形.又∵AB=BC,∴四边形ABCD是菱形.
已知：如图，四边形ABCD中,AB=BC=CD=AD.求证：四边形ABCD是菱形.
四条边都相等的四边形是菱形.
几何语言：∵在四边形ABCD中，AB=BC=CD=AD，
∴四边形 ABCD是菱形.
∵AB=BC=CD=DA
∴四边形ABCD是菱形
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
证明：连接AC , BD.
∵四边形ABCD是矩形，
∵点E , F , G , H为各边中点，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形.
例 如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形.
利用边相等判断四边形是菱形
∴ ,
如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于点E，连接AE、CD.求证：四边形ADCE是菱形.
∵ MN是AC的垂直平分线,∴AD=CD，OA=OC，AE=CE.∵ CE∥AB，∠DAO=∠ECO. ∴ △ADO ≌ △CEO .∴ AD=CE .∴AD=CD=CE=AE.∴四边形ADCE是菱形.
如图，在△ABC中，D , E分别是AB , AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF.(1)求证：四边形BCFE是菱形；
(1)证明：∵D , E分别是AB , AC的中点，∴DE∥BC且2DE＝BC.又∵BE＝2DE，EF＝BE，∴EF＝BC，EF∥BC.∴四边形BCFE是平行四边形．又∵EF＝BE，∴四边形BCFE是菱形；
菱形性质和判定的综合应用
(2)解：∵∠BCF＝120°，∴∠EBC＝60°.∴△EBC是等边三角形.过点E作EH⊥BC, 则HE= ,∴菱形的边长为4，高为 ，∴菱形的面积为 .
(2)若CE＝4，∠BCF＝120°，求菱形BCFE的面积．
判定一个四边形是菱形时，要结合条件灵活选择方法．如果可以证明四条边相等，可直接证出菱形；如果只能证出一组邻边相等或对角线互相垂直，可以先尝试证出这个四边形是平行四边形．
如图，在平行四边形ABCD中，AC平分∠DAB，AB=2，求平行四边形ABCD的周长.
解：∵四边形ABCD为平行四边形，∴AB∥CD.∴∠BAC=∠ACD.∵AC平分∠DAB，∴∠DAC=∠BAC.∴∠DAC=∠ACD.∴AD=DC.∴四边形ABCD为菱形.∴四边形ABCD的周长=4×2=8．
如图，AC＝8，分别以A , C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D．依次连接A,B,C,D，连接BD交AC于点O．（1）判断四边形ABCD的形状并说明理由；（2）求BD的长．
解：（1）四边形ABCD为菱形；由作法,得AB＝AD＝CB＝CD＝5，所以四边形ABCD为菱形；（2）∵四边形ABCD为菱形，在Rt△AOB中，OB＝ ，
∴OA＝OC＝4，OB＝OD，AC⊥BD，
1.下列命题中正确的是（ ）A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
2.下列条件中，不能判定四边形ABCD为菱形的是（ ）A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DAC.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
证明：∵ ∠1= ∠2, 又∵AE=AC,AD=AD, ∴ △ACD≌ △AED (SAS). 同理△ACF≌△AEF(SAS) . ∴CD=ED, CF=EF. 又∵EF=ED, ∴四边形ABCD是菱形.
5.如图,在△ABC中, AD是角平分线,点E , F分别在AB , AD上,且AE=AC,EF = ED.求证：四边形CDEF是菱形.
∴CD=ED=CF=EF.
如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm.将△ABC沿射线BC方向平移10cm，得到△DEF，A，B，C的对应点分别是D，E，F，连接AD.求证：四边形ACFD是菱形．
由平移变换的性质,得CF＝AD＝10cm，DF＝AC.∵∠B＝90°，AB＝6cm，BC＝8cm，∴AC＝DF＝AD＝CF＝10cm.∴四边形ACFD是菱形．
∴ .
已知：如图,□ ABCD的对角线AC的垂直平分线与边AD，BC分别交于E，F．求证：四边形AFCE是菱形.
∴AO=CO, ∠AOE=90°.
∴∠FOC=∠AOE=90°.
∴ AD∥BC. ∴AE∥FC.
∴∠AEO=∠CFO.
∴△AEO≌△CFO.
∴四边形AFCE是平行四边形.
∴四边形AFCE是菱形.
有一组邻边相等的平行四边形是菱形
运用定理进行计算和证明