数学八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.1 矩形一等奖ppt课件

互动导学内容安排

教学环节

教师活动

学生活动

设计意图

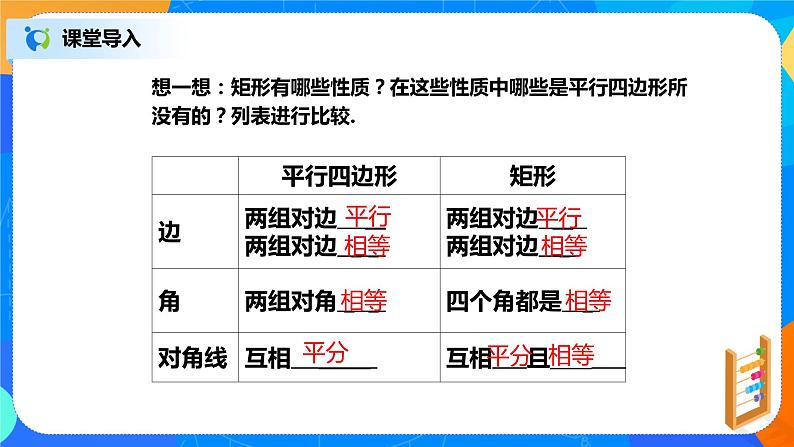
课堂导入(约5分钟)

一、知识回顾

想一想：矩形有哪些性质？在这些性质中哪些是平行四边形所没有的？列表进行比较。

我们知道如何判定一个四边形是平行四边形，平行四边和矩形有很多相似之处，那么它们的判定有什么相似之处呢？本节课我们一起来学习。

除此之外，还有没有其他的判定方法？

根据老师的提问，回顾学过的知识点。

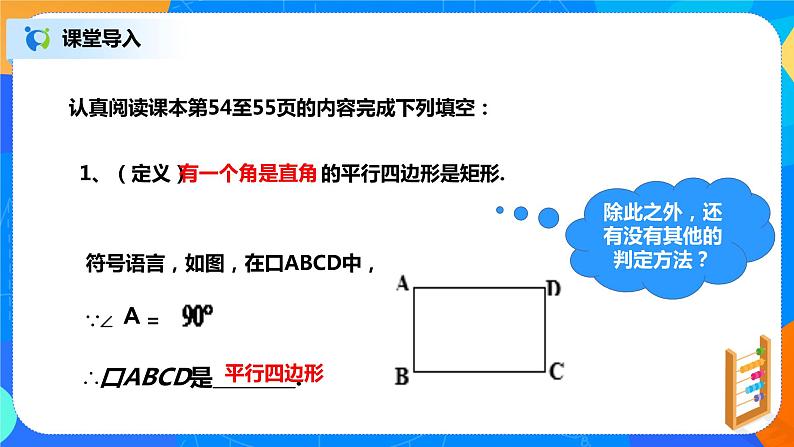
认真阅读课本第54至55页的内容完成下列填空：

1.（定义）  有一个角是直角  的平行四边形是矩形。

符号语言，如图，在平行四边形ABCD中，

∵∠ A＝90°

∴平行四边形ABCD是  平行四边形  。

理解几何知识的内存联系，感悟性质定理与判定定理之间的关系。

探究新知(16—18分钟)

1．矩形的判定

在日常生活中，我们经常能看到这样的场景。工人师傅为了检验两组对边相等的四边形窗框是否成矩形，一种方法是量一量这个四边形的两条对角线长度，如果对角线长相等，则窗框一定是矩形，你知道为什么吗？

大家能证明这个猜想吗？

证明时，我们需要结合矩形的定义，从证明一个角为90°入手，再根据平行四边形的性质，从而找出已知条件。大家动手试一下吧。

课件展示证明过程。

由此，我们得到了矩形的另一个判定定理：

对角线相等的平行四边形是矩形。

在上一节课的学习当中，我们知道一个矩形的四个角都是直角，如果将这个命题反过来，即它的逆命题还成立吗？如果上述逆命题成立，那么进一步说，至少有几个角是直角的四边形是矩形呢？

按照刚刚的判定定理的证明，大家能有什么样的思路呢？（学生回答证明）

课件展示证明过程。

矩形的另一个判定定理：有三个角是直角的四边形是矩形。

课本例2讲解。

今天我们主要学习了矩形的判定定理，现在，大家来练习一下吧。

【知识巩固】1、□ABCD中，AE、CF、BF、DE分别为四个内角平分线，求证：EGFH是矩形。

解：∵四边形ABCD是平行四边形，

∴∠BAD+∠ABC=180°，

∵AE、BF分别是内角的平分线，

∴∠BAG=∠DAG=∠BAD，∠ABG=∠CBE=∠ABC，

∴∠BAG+∠ABG=（∠BAD+∠ABC）=90°，

同理：∠E=∠F=90°，

∴∠EGF=90°，∴四边形EGFH是矩形。

2、如图，在四边形ABCD中，AB∥CD，∠B=∠D，AE平分∠BAD交BC于E．若AB=2，AE=2，试判断四边形ABCD的形状，并说明理由。

解：四边形ABCD是矩形；理由如下：

∵AB∥CD，

∴∠B+∠C=180°，

∵∠B=∠D，

∴∠D+∠C=180°，

∴AD∥BC，

∴四边形ABCD是平行四边形，∠DAE=∠AEB，

∵AE平分∠BAD，

∴∠BAE=∠DAE，

∴∠BAE=∠AEB，

∴BE=AB=2，

∵AB2+BE2=22+22=8=（2 ）2=AE2，

∴△ABE是直角三角形，∠B=90°，

∴四边形ABCD是矩形。

3、如图，在△AEC、△BED中，∠AEC=∠BED=90°，AC、BD相交于点O，且O是AC、BD的中点．求证：四边形ABCD是矩形．

解：连接EO，

∵O是AC、BD的中点，

∴AO=CO，BO=DO，

在Rt△EBD中，

∵O为BD中点，

∴EO=BD，

在Rt△AEC中，∵O为AC中点，

∴EO=AC，

∴AC=BD，

又∵四边形ABCD是平行四边形，

∴平行四边形ABCD是矩形。 

猜想：工人师傅是怎样知道窗户是矩形的呢?

猜想：除度量角度之外,木工师傅度量什么也能知道做好的门框是矩形呢?

猜想：有三个角是直角的四边形是矩形 。

我们该如何证明这个猜想呢？

围绕逆命题是否成立展开探究活动。

掌握几何证明题的思路。

巩固提升(21分钟)

1、四边形ABCD的对角线AC、BD互相平分，要使它成为矩形，需要添加的条件是（　B　）

A．AB=CD B．AC=BD C．AB=BC D．AC⊥BD

2、下列命题中，假命题是（　C　）

A．有一组对角是直角且一组对边平行的四边形是矩形

B．有一组对角是直角且一组对边相等的四边形是矩形

C．有两个内角是直角且一组对边平行的四边形是矩形

D．有两个内角是直角且一组对边相等的四边形是矩形

3、有下列说法：①四个角都相等的四边形是矩形；②有一组对边平行，有两个角为直角的四边形是矩形；③两组对边分别相等且有一个角为直角的四边形是矩形；④对角线相等且有一个角是直角的四边形是矩形；⑤对角线互相平分且相等的四边形是矩形．其中，正确的个数是（　B　）

A．2个 B．3个 C．4个 D．5个

4、如图，在△ABC中，AD为BC边上的中线，延长AD至E，使DE=AD，连接BE，CE。

（1）请判断四边形ABEC的形状；

（2）当△ABC满足什么条件时，四边形ABEC是矩形？

解：（1）四边形ABEC是平行四边形；理由如下：

∵AD为BC边上的中线，∴BD=CD，

∵DE=AD，

∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形）；

（2）当∠BAC=90°，四边形ABEC是矩形；理由如下：

∵四边形ABEC是平行四边形，∠BAC=90°，

∴四边形ABEC是矩形（有一个角是直角的平行四边形是矩形）

【拓展提升】1、如图，在平行四边形ABCD中，角线AC、BD相交于点O，动点E以1个单位每秒的速度从点A出发沿AC向运动，点F同时以1个单位每秒的速度从点C发沿CA方向运动，若AC=12，BD=8，求出经过几秒后，四边形BPDQ是矩形？

解： 设经过t秒后，四边形BPDQ是矩形；

则AE=CF=t，

∵四边形ABCD是平行四边形，

∴OA=OC= AC=6，OB=OD=BD=4，

∴OE=OF，

∴四边形BFDE是平行四边形，

当EF=BD，即OE=OD时，四边形BFDE是矩形，

此时6-t=4，或t-6=2，

解得：t=2，或t=8，

即经过2秒或8秒后，四边形BPDQ是矩形。

独立完成，

应用矩形的判定定理。

课堂小结(约3分钟)

矩形的判定：

（1）定义： 有一个角是直角的平行四边形是矩形。

（2）对角线相等的平行四边形是矩形。

（3）有三个角是直角的四边形是矩形。

课后作业

教学反思

本节课主要是关于判定的推导，采用的教学方法是以实际物体及实例进行开展，通过不断创设有效的教学情境刺激学生的思维，与学生进行真诚的交流，让学生在整堂课中能在不断出现的问题及不断被自己"聪明"的解决问题的成功喜悦中进行学习，享受学习的乐趣，从而获得好的教学效果。