人教版八年级下册18.2.1 矩形精品ppt课件

互动导学内容安排

教学环节

教师活动

学生活动

设计意图

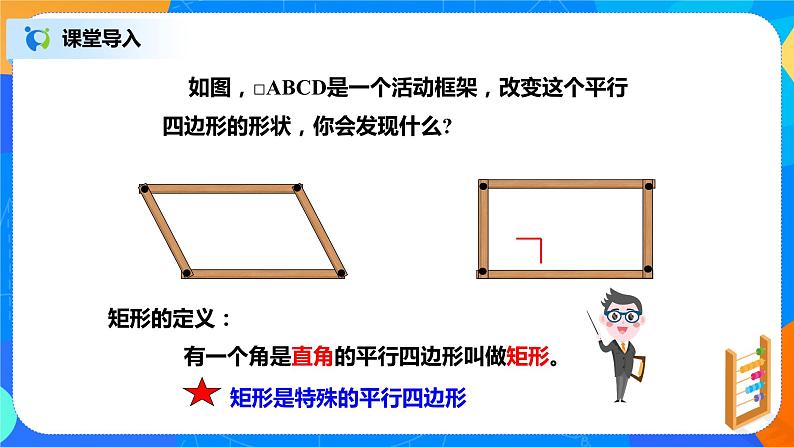
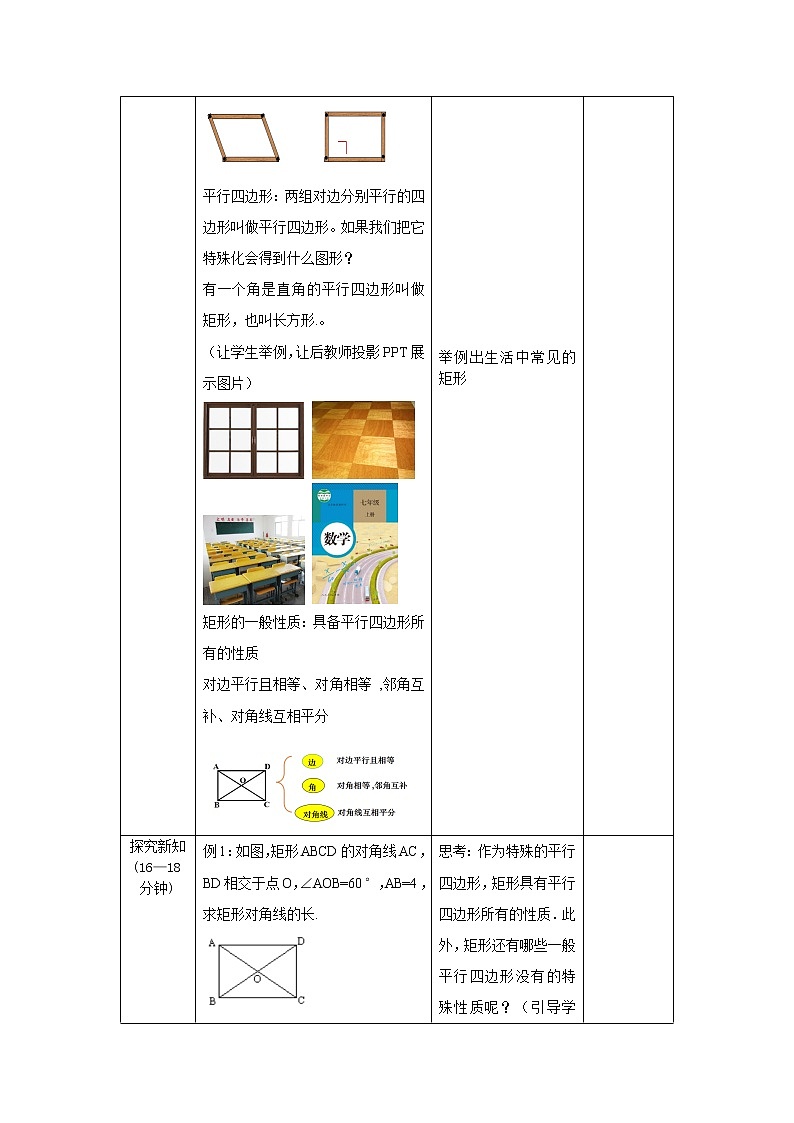
课堂导入(约5分钟)

1.什么叫平行四边形？

两组对边分别平行的四边形叫做平行四边形。

2.平行四边形有哪些性质？

①边：对边平行且相等。

②角：对角相等且邻角互补。

③对角线：互相平分。

如图，□ABCD是一个活动框架，改变这个平行四边形的形状，你会发现什么?

平行四边形：两组对边分别平行的四边形叫做平行四边形。如果我们把它特殊化会得到什么图形？

有一个角是直角的平行四边形叫做矩形，也叫长方形.。

（让学生举例，让后教师投影PPT展示图片）

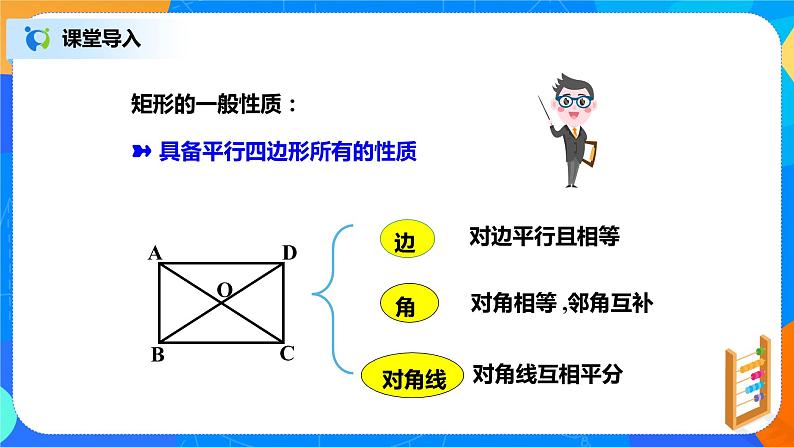
矩形的一般性质：具备平行四边形所有的性质

对边平行且相等、对角相等 ,邻角互补、对角线互相平分

回答问题。

举例出生活中常见的矩形

复习巩固，为新课辅设。

探究新知(16—18分钟)

例1：如图，矩形ABCD的对角线AC，BD相交于点O，∠AOB=60°，AB=4，求矩形对角线的长.

分析：因为矩形是特殊的平行四边形，所以它具有对角线相等且互相平分的特殊性质，根据矩形的这个特性和已知，可得△OAB是等边三角形，因此对角线的长度可求．

解：∵四边形ABCD是矩形，

∴AC与BD相等且互相平分．

∴OA=OB．

又∠AOB=60°，

∴△OAB是等边三角形．

∴矩形的对角线长AC=BD = 2OA=2×4=8（cm）

例2：如图，在△ABC中，∠BAC＞90°，DC⊥DB，BE⊥EC，F为BC上的一个动点，猜想：当F为于BC上的什么位置时，△FDE是等腰三角形，并证明你的猜想是正确的。

当F为BC上的中点时，△FDE是等腰三角形，

证明：∵DC⊥DB，F为BC上的中点，

∴DF=BC

∵BE⊥EC，F为BC上的中点，

∴EF=BC

∴DF=EF，

∴△FDE是等腰三角形

思考：作为特殊的平行四边形，矩形具有平行四边形所有的性质．此外，矩形还有哪些一般平行四边形没有的特殊性质呢？（引导学生类比平行四边的性质进行学习，然后提出猜想）。

猜想（1）矩形的四个角都是直角

猜想（2）矩形的对角线相等

认真阅读课本第52页至53页的内容，完成下面证明过程。

猜想1：矩形的四个角都是直角。

巩固提升(21分钟)

1.如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，EF=7，BC=10，则△EFM的周长是（   ）A

A．17      B．21      C．24       D．27

2.如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为（   ）B

A．（0，-） B．（0，-） C．（0，-） D．（0，-）

3.如图，在矩形ABCD中，AD=12，AB=7，DF平分∠ADC，AF⊥EF。

（1）求证：AF=EF；（2）求EF长。

（1）证明：∵四边形ABCD是矩形，

∴∠B=∠C=∠ADC=90°，AB=DC=7，BC=AD=12，

∴∠BAF+∠AFB=90°，

∵DF平分∠ADC，

∴∠ADF=∠CDF=45°，

∴△DCF是等腰直角三角形，

∴FC=DC=7，

∴AB=FC，

∵AF⊥EF，

∴∠AFE=90°，

∴∠AFB+∠EFC=90°，

∴∠BAF=∠EFC，

在△ABF和△FCE中，

∠BAF＝∠EFC；AB＝FC；∠B＝∠C，

∴△ABF≌△FCE（ASA），∴EF=AF；

（2）解：BF=BC-FC=12-7=5，

在Rt△ABF中，由勾股定理得：AF= = =，

则EF=AF=。

4.已知：如图 ，矩形 ABCD，AB长8 cm ，对角线比AD边长4 cm．求AD的长及点A到BD的距离AE的长．

分析：（1）因为矩形四个角都是直角，因此矩形中的计算经常要用到直角三角形的性质，而此题利用方程的思想，解决直角三角形中的计算，这是几何计算题中常用的方法．

略解：设AD=xcm，则对角线长（x+4）cm，在Rt△ABD中，由勾股定理：，解得x=6． 则 AD=6cm．

（2）“直角三角形斜边上的高”是一个基本图形，利用面积公式，可得到两直角边、斜边及斜边上的高的一个基本关系式： AE×DB＝ AD×AB，解得 AE＝ 4.8cm．

5.已知：如图，矩形ABCD中，E是BC上一点，DF⊥AE于F，若AE=BC． 求证：CE＝EF．

   分析：CE、EF分别是BC，AE等线段上的一部分，若AF＝BE，则问题解决，而证明AF＝BE，只要证明△ABE≌△DFA即可，在矩形中容易构造全等的直角三角形．

证明：∵四边形ABCD是矩形，

∴∠B=90°，且AD∥BC．∴∠1=∠2．

∵DF⊥AE，∴∠AFD=90°．

 ∴∠B=∠AFD．又AD=AE，

∴△ABE≌△DFA（AAS）．

∴AF=BE．

∴EF=EC．

此题还可以连接DE，证明△DEF≌△DEC，得到EF＝EC．

独立完成

巩固矩形性质定理

课堂小结(约3分钟)

课后作业

教材P53，练习第2题．

教学反思

让学生体会直角三角形斜边上的中线等于斜边的一半证明过程，能够帮助学生掌握几何证明的思路和方法。