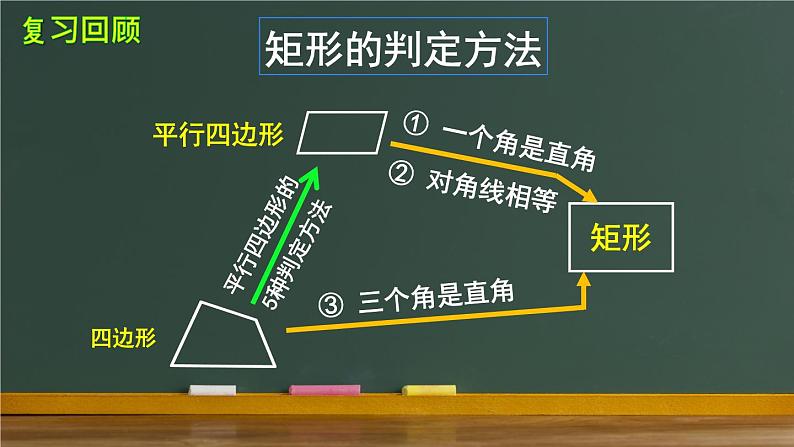
初中数学人教版八年级下册18.2.2 菱形教学ppt课件

这是一份初中数学人教版八年级下册18.2.2 菱形教学ppt课件，共21页。PPT课件主要包含了学习目标，矩形的判定方法，菱形的定义，探究菱形的判定方法，菱形的性质，菱形的判定定理，菱形的四条边都相等，菱形的判定方法，应用练习巩固知识等内容，欢迎下载使用。

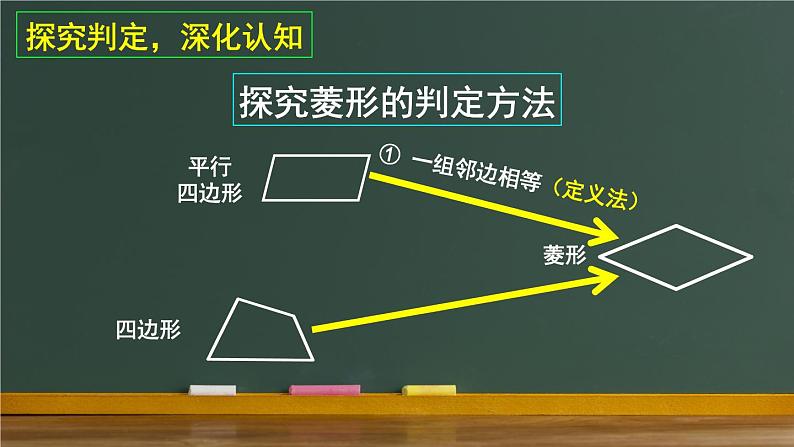
有一组邻边相等的平行四边形叫做菱形.
∵ 四边形ABCD是平行四边形
∴ 四边形ABCD是菱形.
① 一组邻边相等（定义法）
对角线互相垂直的平行四边形是菱形.
菱形的对角线互相垂直.
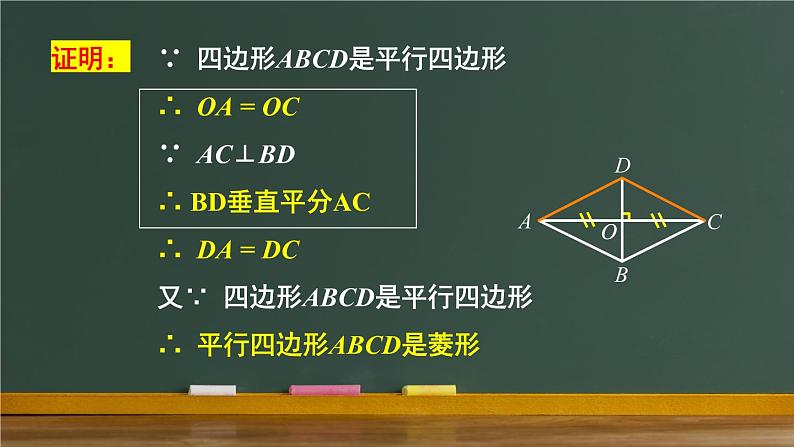
猜想1 对角线互相垂直的平行四边形是菱形
证明： ∵ 四边形ABCD是平行四边形 ∴ OA = OC ∵ AC⊥BD ∴ BD垂直平分AC ∴ DA = DC 又∵ 四边形ABCD是平行四边形 ∴ 平行四边形ABCD是菱形
在平行四边形ABCD中，∵ AC⊥BD，∴ 平行四边形ABCD是菱形.
猜想2 四条边相等的四边形是菱形
已知：如图，在四边形ABCD中，AB = BC = CD = AD. 求证：四边形ABCD是菱形.
证明：∵ AB = BC = CD = AD，∴ AB = CD， BC = AD.∴ 四边形ABCD是平行四边形.又 AB = BC，∴ 四边形ABCD是菱形.
菱形的判定定理：四条边相等的四边形是菱形.
∵ AB = BC = CD = AD，∴ 四边形ABCD是菱形.
（1）有一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四条边相等的四边形是菱形。
例 如图， ABCD的对角线AC，BD相交于点O，且AB = 5，AO = 4，BO = 3.求证： ABCD是菱形.
证明：∵ 32+42=25，52=25 ∴∴ △AOB是直角三角形∴ ∠AOB=90°∴ AC⊥BD又∵ ABCD是平行四边形∴ ABCD是菱形
例 如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD.求证：四边形ABCD是菱形.
证明：∵ AE∥BF， ∴ ∠1 =∠2.∵ AC平分∠BAD，∴ ∠1 =∠3.∴ ∠2 =∠3.∴ AB = BC.
证明：同理 AB = AD. ∴ AD = BC.∵ AD∥BC， ∴ 四边形ABCD是平行四边形.又 AB = AD，∴ 四边形ABCD是菱形.