人教版八年级下册18.2.2 菱形示范课课件ppt

第十八章  平行四边形

18.2.2 菱形

第2课时  菱形的判定

一、 教学目标

探究菱形的判定方法，掌握菱形的判定定理，了解菱形在实际问题中的应用．

二、 重点难点

重点

理解并掌握菱形的判定定理．

难点

发展学生的逻辑推理能力．

三、 教学设计

（一）   新知导入

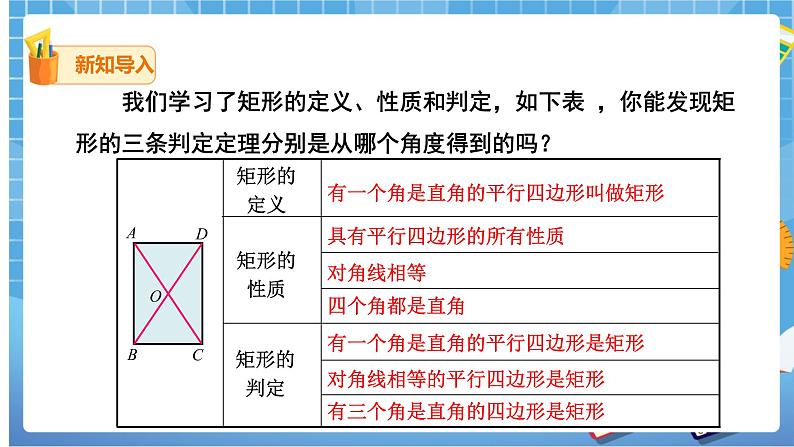
我们学习了矩形的定义、性质和判定，如下表 ，你能发现矩形的三条判定定理分别是从哪个角度得到的吗？

（教师提问，学生回答，PPT2逐条展示结果）

菱形的定义与性质如下表．你认为可以从哪些角度思考菱形的判定条件？

（教师提问，学生回答，PPT2逐条展示结果，提出问题：  你的想法正确吗？

如何证明你的猜想？  ）

（二）   新知讲解

（PPT4展示）

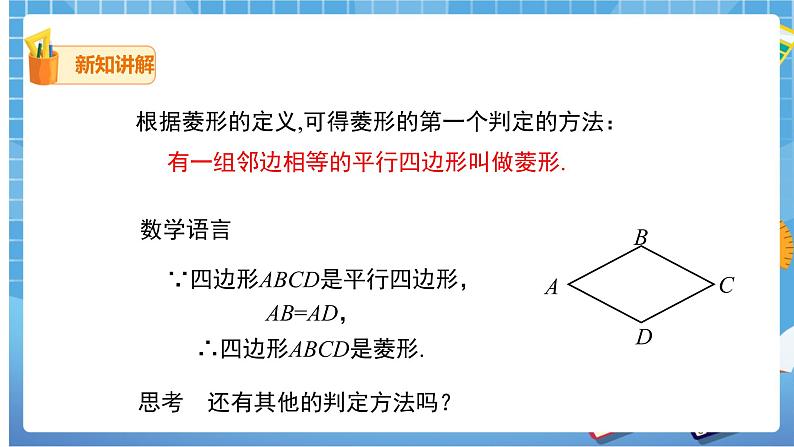
根据菱形的定义,可得菱形的第一个判定的方法：

有一组邻边相等的平行四边形叫做菱形.

数学语言

∵四边形ABCD是平行四边形，

AB=AD，

∴四边形ABCD是菱形.

思考    还有其他的判定方法吗？

类比学习平行四边形和矩形的判定过程，研究菱形性质定理的逆命题,你能找到菱形判定的其他方法吗？

猜想1：对角线互相垂直的平行四边形是菱形

猜想2：四条边都相等的四边形是菱形

证一证

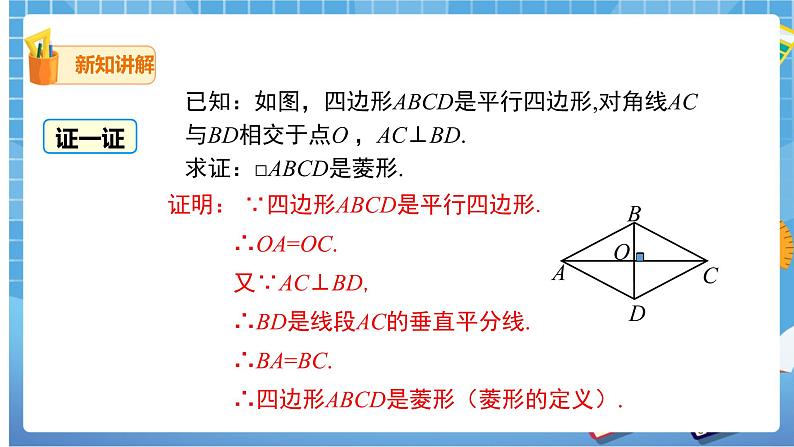
已知：如图，四边形ABCD是平行四边形,对角线AC与BD相交于点O ，AC⊥BD.

求证：□ABCD是菱形.

（教师引导学生证明猜想1.分组讨论，协同解决问题，组长汇报证明过程，教师点评，PPT6展示证明过程）

归纳总结

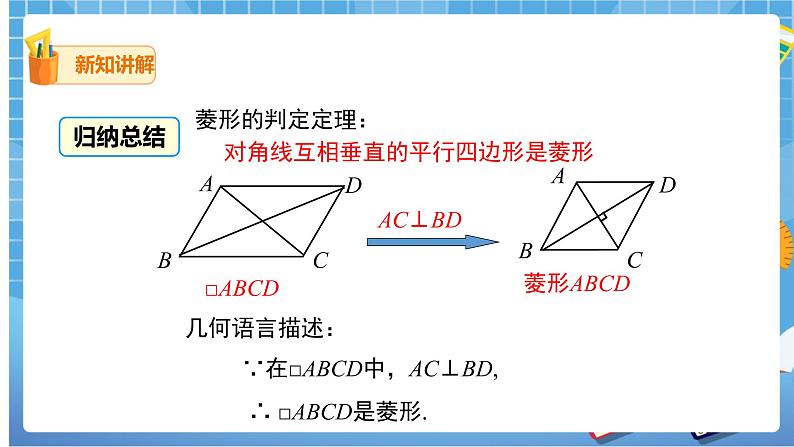
菱形的判定定理：

对角线互相垂直的平行四边形是菱形

（PPT展示结果，教师强调学生自己书写几何语言）

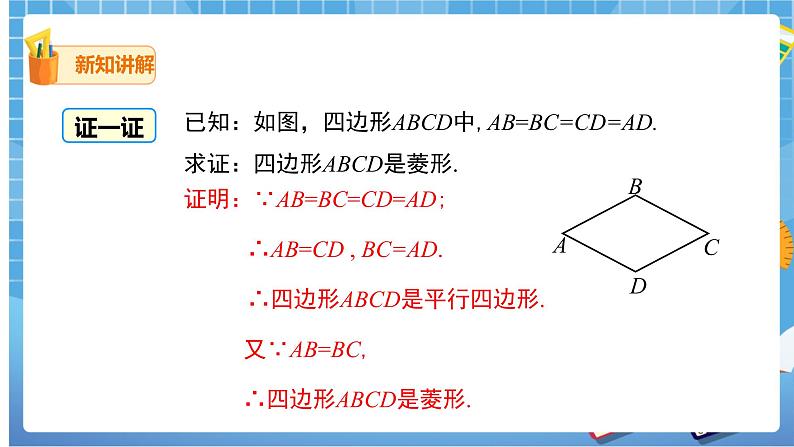
证一证

已知：如图，四边形ABCD中,AB=BC=CD=AD.

求证：四边形ABCD是菱形.

（教师引导学生证明猜想2.分组讨论，协同解决问题，组长汇报证明过程，教师点评，PPT8展示证明过程）

归纳总结

菱形的判定定理：

四条边都相等的四边形是菱形

（PPT9展示结果，教师强调学生自己书写几何语言）

例1   如图，   ABCD的两条对角线AC、BD相交于点O，AB=5，AO=4，BO=3.

    求证：四边形ABCD是菱形.

（学生分组练习，组长汇报结果，PPT10展示解答过程）

例2  如图,在△ABC中, AD是角平分线,点E、F分别在 AB、 AD上,且AE=AC,

EF = ED.

    求证：四边形CDEF是菱形.     

（学生分组练习，组长汇报结果，PPT11展示解答过程）

例3    如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，

求证：四边形EFGH是菱形.

（学生分组练习，组长汇报结果，PPT12展示解答过程）

（三）   课堂练习

1.在四边形ABCD中，对角线AC，BD互相平分，若添加一个条件使得四边形ABCD是菱形，则这个条件可以是                   （ 　 ）

 A．∠ABC=90°

 B．AC⊥BD

 C．AB=CD

D．AB∥CD

2.下列命题中正确的是                       （      ）

A.一组邻边相等的四边形是菱形

B.三条边相等的四边形是菱形

C.四条边相等的四边形是菱形

D.四个角相等的四边形是菱形

3.如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ACED为菱形的是（　　）

   A．AB=BC         B．AC=BC   

   C．∠B=60°     D．∠ACB=60°

4.如图，矩形ABCD的对角线相交于点O，DE∥AC,CE ∥BD.

求证：四边形OCED是菱形.

（四）   拓展提高

1.如图,在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线交BC于点E，连接EF．

（1）求证：四边形ABEF为菱形；

（2）AE，BF相交于点O，若BF=6，AB=5，求AE的长．

（1）证明：由尺规作∠BAF的平分线的过程可得AB=AF，∠BAE=∠FAE，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠FAE=∠AEB，

∴∠BAE=∠AEB，

∴AB=BE，

∴BE=FA，

∴四边形ABEF为平行四边形，

∵AB=AF，

∴四边形ABEF为菱形；

解：∵四边形ABEF为菱形，

∴AE⊥BF，BO=    FB=3，AE=2AO，

在Rt△AOB中，由勾股定理得AO =4，

∴AE=2AO=8．

四、 课堂总结

六、作业设计

　　　　　　　　　　　　　课后作业：课本60页习题18.2第6题。