初中数学人教版八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形一等奖课件ppt

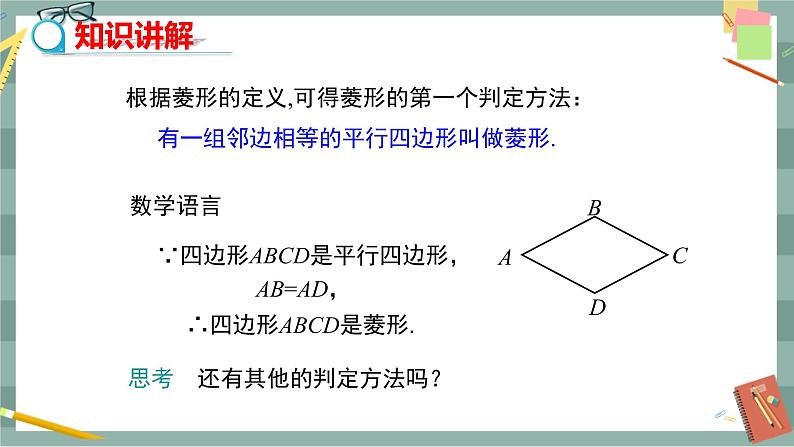
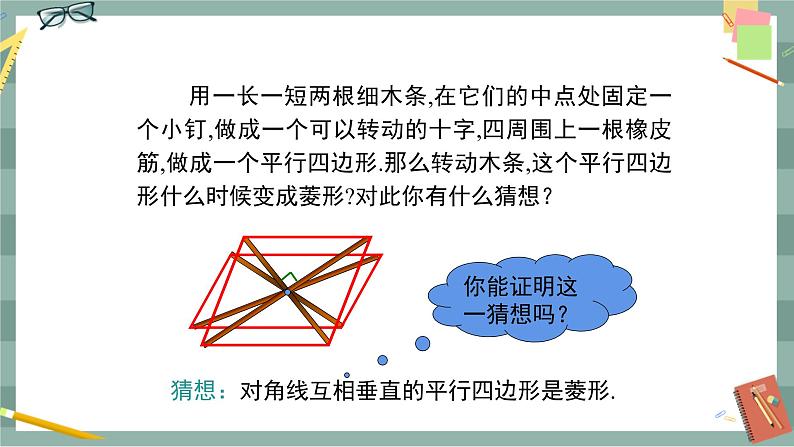
教学目标

1.掌握菱形判定定理的证明并会灵活运用.

2.经历探索、猜想、证明的过程，从中体会探索结论的思考方法，理解对猜想进行证明的必要性，不断感受合情推理是人们正确认识事物的重要途径.

3.通过菱形与矩形判定方法的类比，进一步体会类比思想方法的作用.

教学重难点

重点：菱形判定定理的证明及应用.

难点：菱形判定定理的综合应用.

教学过程

导入新课

导入1：

图1

问题1：两张宽度相等的纸条，交叉在一起，重叠部分（图1）是什么图形？你是怎样判断的？

师生活动：学生讨论后，学生代表发言，教师板书.它是菱形.因为宽度相等的纸条对边都是平行的，首先构成了平行四边形，还能观察出邻边是相等的，根据菱形的定义可判断是菱形.（作出判断容易，但证明有难度，若不能证出也无妨，可留待后解，只要能引出问题2即可）

问题2：运用菱形的定义进行菱形的判定，应具备几个条件？

师生活动：学生讨论后，学生代表发言，教师板书.应具备两个条件，一要看是不是平行四边形，二要看邻边是否相等，即一组邻边相等的平行四边形是菱形.

问题3：要判定一个四边形是菱形，除根据定义判定外，还有其他的判定方法吗？

导入课题：菱形的判定.

导入2：

1.平行四边形、矩形的判定方法是什么？

2.菱形的概念及性质是什么？

探究新知

教师：菱形是有一组邻边相等的平行四边形，因此在识别一个四边形是不是菱形时，可首先看这个四边形是不是平行四边形，再看它两邻边是不是相等，这种用“定义”识别的方法是最重要和最基本的识别方法.

几何语言：

在ABCD中，∵ AB＝BC，∴ 四边形ABCD是菱形.

教师：今天我们类比平行四边形、矩形的判定方法继续研究菱形的判定方法.

活动1：探讨对角线互相垂直的平行四边形是菱形.

教师：大家都知道，菱形的特别之处在于对角线互相垂直，那么能否从对角线的特点来识别菱形呢？

如图2所示，用一长一短两根木条，在它们的中点处固定一个小钉，做成一个可转动的十字，四周围上一根橡皮筋，做成一个四边形.转动木条，这个四边形什么时候变成菱形？

图2

学生猜想1：对角线互相垂直的平行四边形是菱形.

（先让学生根据菱形对角线的特殊性猜想，并进行证明，从而得出一种判定方法.在探索的过程中，让学生自己写出已知、求证和证明，培养他们的能力）

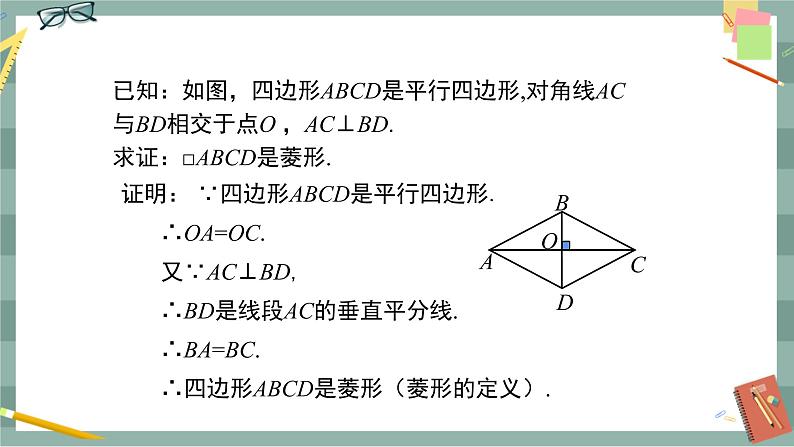
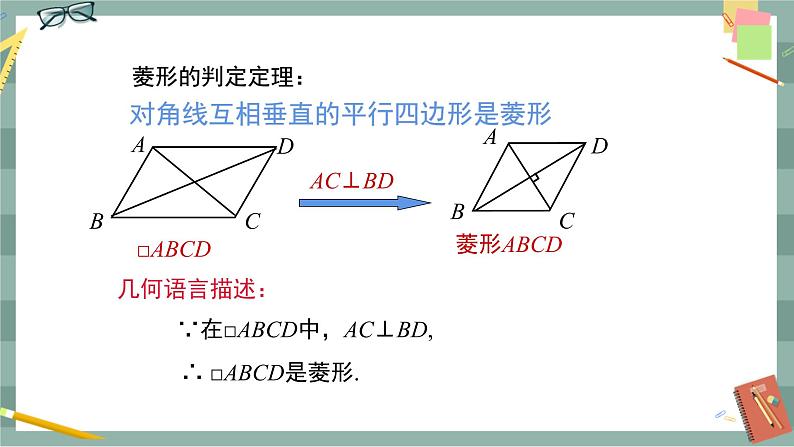
图3

已知：如图3所示，在ABCD中，对角线AC⊥BD.

求证：四边形ABCD是菱形.

分析：要证明ABCD是菱形，可以利用垂直平分线的性质证明有一组邻边相等.

证明：∵ 四边形ABCD是平行四边形，∴ AO＝CO.

∵ AC⊥BD，∴ DA＝DC.∴ ABCD是菱形.

定理：对角线互相垂直的平行四边形是菱形.

几何语言：在ABCD中，∵ AC⊥BD，

∴ABCD是菱形.

注意此方法包括两个条件：（1）平行四边形；（2）两条对角线互相垂直.

活动2：探讨四条边相等的四边形是菱形.

教师：菱形的特别之处在于它的邻边相等，能否从边的特点来识别菱形呢？

如图4所示，先画两条等长的线段AB，AD，然后分别以B，D为圆心，AB长为半径画弧，得到两弧的交点C，连接BC，CD，就得到了一个四边形，猜一猜，这是一个怎样的四边形.说出你的理由.

图4　　　　　 　　　图5

学生猜想2：四条边相等的四边形是菱形.

已知：如图5所示，在四边形ABCD中， AB＝BC＝CD＝DA.

求证：四边形ABCD是菱形.

分析：利用菱形的定义和两组对边分别相等的四边形是平行四边形，可使问题得证.

证明：∵ AB＝BC＝CD＝DA，∴ AB＝CD，BC＝DA，

∴ 四边形ABCD是平行四边形.

∵ AB＝AD，∴ 四边形ABCD是菱形.

定理：四条边相等的四边形是菱形.

几何语言：在四边形ABCD中，∵ AB＝BC＝CD＝AD，∴ 四边形ABCD是菱形.

新知应用

图6

例1　如图6所示，ABCD的对角线AC，BD相交于点O，且AB＝5，AO＝4，BO＝3.

求证：ABCD是菱形.

分析：因为四边形ABCD为平行四边形，所以只需利用勾股定理的逆定理证明对角线互相垂直即可.

证明：∵ AB＝5，AO＝4，BO＝3，

∴ AB2＝AO2+BO2，

∴ △OAB是直角三角形，∠AOB＝90°，

∴ AC⊥BD.∴ABCD是菱形.

图7

例2　如图7所示，顺次连接矩形ABCD各边中点，得到四边形EFGH.求证：四边形EFGH是菱形.

证明：连接AC，BD.

∵ 四边形ABCD是矩形，

∴ AC＝BD.

∵ 点E，F，G，H为各边中点，

∴ EF＝GH＝BD，FG＝EH＝AC，

∴ EF＝FG＝GH＝HE，

∴ 四边形EFGH是菱形.

课堂小结

菱形可根据下列方法进行识别.

布置作业

教材第58页练习第1，2，3题.

板书设计