数学22.3 实际问题与二次函数课时训练

这是一份数学22.3 实际问题与二次函数课时训练，共9页。试卷主要包含了心理学家研究发现，给出下列结论等内容，欢迎下载使用。

22.3《实际问题与二次函数》拓展练习


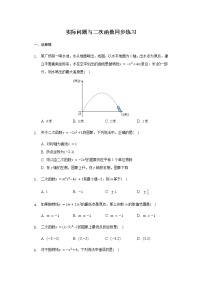
1.太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法.为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻.在一定条件下,直杆的太阳影子长度l(单位:米)与时刻t(单位:时)的关系满足函数关系式l=at2+bt+c(a,b,c是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是( )





B.13 D.13.5





2.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,则右轮廓DFE所在抛物线的解析式为( )





A.y=(x+3)2 B.y=(x-3)2 C.y=-(x+3)2 D.y=-(x-3)2





3.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .






































4.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+,则下列结论:


(1)柱子OA的高度为 m;


(2)喷出的水流距柱子1 m处达到最大高度;


(3)喷出的水流距水平面的最大高度是2.5 m;


(4)水池的半径至少要2.5 m才能使喷出的水流不至于落在水池外.


其中正确的有( )





A.1个 B.2个 C.3个 D.4个





5.心理学家研究发现:一般情形下,在一节40分钟的课中,学生的注意力随教师讲课的时间变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持为理想的稳定状态,随后学生的注意力开始分散.经过试验分析,知学生的注意力指数y随时间x(分钟)的变化规律为y=


有一道数学竞赛题需要讲解16.5分钟,为了使效果更好,要求学生的注意力指数最低值达到最大.那么,教师经过适当安排,应在上课的第 分钟开始讲解这道题.





6.如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80 m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为 m.


























7.如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-k)2+h.已知球与O点的水平距离为6 m时,达到最高2.6 m,球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m,则下列判断正确的是( )





A.球不会过球网 B.球会过球网但不会出界


C.球会过球网并会出界 D.无法确定





8.某企业要生产一批产品,按要求必须在15天内完成,已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足函数关系y=2x+18(0≤x≤15).经调研,工人甲生产该产品的成本p(元/件)与第x天的函数关系图象如图所示.


(1)求p与x之间的函数表达式;


(2)若工人甲第x天创造的利润为w元,求w与x之间的函数关系式,并求出在第几天时,利润最大,最大利润是多少?




































































9.如图,有一块边长为6 cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )





A. cm2 B. cm2 C. cm2 D. cm2





10.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室总占地面积最大为 m2.








11.荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间t(天)之间的函数关系为p=日销售量y(千克)与时间t(天)之间的函数关系如图所示:





(1)求日销售量y与时间t的函数关系式;


(2)哪一天的日销售利润最大?最大利润是多少?


(3)该养殖户有多少天日销售利润不低于2 400元?


(4)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.























12.某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长为6 m,鱼隐约在水面了,估计鱼离鱼竿支点有8 m,此时鱼竿鱼线呈一个平面,且鱼线与水平面夹角α恰好为60°,以鱼竿支点为原点,则鱼竿所在抛物线的解析式为 .








13.某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:


(1)月销量y(件)与售价x(元)的关系满足:y=-2x+400;


(2)工商部门规定销售价x满足:70≤x≤150(计算月利润时不考虑其他成本).给出下列结论:


①这种文化衫的月销量最小为100件;


②这种文化衫的月销量最大为260件;


③销售这种文化衫的月利润最小为2 600元;


④销售这种文化衫的月利润最大为9 000元.


其中正确的是 (把所有正确结论的序号都填上).










































































参考答案


1.答案为：C；


解析：把(12,0.6)、(13,0.35)、(14,0.4)代入l=at2+bt+c中,


得解得∴l=0.15t2-4t+27.


∵0.15>0,∴l有最小值,当t=-=≈13.33时,该地影子最短.故选C.


2.答案为：B；


解析：∵高CH=1 cm,BD=2 cm,且B、D关于y轴对称,∴D点坐标为(1,1),


∵AB∥x轴,AB=4 cm,最低点C在x轴上,∴A,B关于直线CH对称,


∴左边抛物线的顶点C的坐标为(-3,0),


∴右边抛物线的顶点F的坐标为(3,0),


设右边抛物线的解析式为y=a(x-3)2,


把D(1,1)代入得1=a×(1-3)2,解得a=,


∴右边抛物线的解析式为y=(x-3)2,故选B.


3.答案为：0

解析：设每天缴纳电商平台推广费用后的利润为W元,则W=(110-40-t)·(20+4t)-a(20+4t)=-4t2+(260-4a)t+1 400-20a.


要使W随t的增大而增大,则-≥30,解得a≤5.∵a>0,∴0

4.答案为：C；


解析：当x=0时,y=,故柱子OA的高度为 m,(1)正确;


∵y=-x2+2x+=-(x-1)2+2.25,∴顶点是(1,2.25),故喷出的水流距柱子1 m处达到最大高度,喷出的水流距水平面的最大高度是2.25 m,故(2)正确,(3)错误;解方程-x2+2x+=0,得x1=-,x2=,故水池的半径至少要2.5 m才能使喷出的水流不至于落在水池外,(4)正确.故选C.


2.答案为：7.5；


解析：设在上课的第x分钟开始讲解这道题,


由题意知4x+60=(x+16.5)2-(x+16.5)+165,整理得x2-219x+1586.25=0,


∴(x-7.5)(x-211.5)=0,∴x=7.5或x=211.5(舍去),


即在上课的第7.5分钟开始讲解这道题,注意力指数最低值达到最大.


3.答案为：15；


解析：∵三块矩形区域的面积相等,∴矩形AEFD面积是矩形BCFE面积的2倍,


∴AE=2BE,设矩形ABCD的面积为y m2,BC=x m,BE=a m,


则AE=2a m,∴8a+2x=80,∴a=-x+10,3a=-x+30,


∴y=x=-x2+30x.


∵a=-x+10>0,∴x<40.y=-x2+30x=-(x-20)2+300(0

∴当x=20时,y有最大值,最大值为300,


当x=20时,a=-x+10=5,∴AB=AE+BE=3a=15 (m).


4.答案为：C；


解析：∵球与O点的水平距离为6 m时,达到最高2.6 m,∴设抛物线为y=a(x-6)2+2.6,


∵抛物线y=a(x-6)2+2.6过点(0,2),∴2=a(0-6)2+2.6,解得a=-,


故y与x的关系式为y=-(x-6)2+2.6,当x=9时,y=-×(9-6)2+2.6=2.45>2.43,


所以球会过球网;当y=0时,-(x-6)2+2.6=0,解得x1=6+2>18,x2=6-2(舍去),


故会出界.故选C.


5.解：(1)当0≤x≤5时,p=40,


当5≤x≤15时,设p=kx+b,


根据题意,得解得则p=x+35,


综上,p=


(2)当0≤x≤5时,w=(60-40)(2x+18)=40x+360,


当x=5时,w取得最大值,最大值为560元;


当5

∴当x=8时,w取得最大值,最大值为578元.


综上所述,w=


工人甲在第8天时创造的利润最大,最大利润为578元.


6.答案为：C；


解析：设筝形较短边为x cm,则较长的边为x cm,


故底面等边三角形的边长为(6-2x)cm,则S=(6-2x)·x·3=-6x2+18x,


故侧面积的最大值为== (cm2).故选C.


7.答案为：75；


解析：设垂直于现有墙的一面墙长为x m,建成的饲养室总占地面积为y m2,


则利用现有墙的长为27+3-3x=(30-3x)m,


∴y=x(30-3x)=-3x2+30x=-3(x-5)2+75.


∵-3<0,∴当x=5时,ymax=75,


即能建成的饲养室总占地面积最大为75 m2.


8.解：(1)设解析式为y=kt+b,将(1,198)、(80,40)代入,


得解得


∴y=-2t+200(1≤t≤80,t为整数).


(2)设日销售利润为w元,则w=(p-6)y.


①当1≤t≤40时,w=(-2t+200)=-(t-30)2+2 450,


∴当t=30时,w最大=2 450;


②当41≤t≤80时,w=(-2t+200)=(t-90)2-100,


∴当t=41时,w最大=2 301.


∵2 450>2 301,∴第30天的日销售利润最大,最大利润为2 450元.


(3)由(2)得当1≤t≤40时,w=-(t-30)2+2 450,


令w=2 400,则-(t-30)2+2 450=2 400,解得t1=20,t2=40.


作出函数w=-(t-30)2+2 450的图象如下,





∴当20≤t≤40时,日销售利润不低于2 400元,


又由(2)知,当41≤t≤80时,w最大=2 301<2 400,


∴t的取值范围是20≤t≤40.


∴该养殖户有21天日销售利润不低于2 400元.


(4)设日销售利润为w元.根据题意,得


w=(-2t+200)=-t2+(30+2m)t+2 000-200m(1≤t≤40).


∴其函数图象的对称轴为t=2m+30,


∵w随t的增大而增大,


∴由二次函数的图象及其性质可知2m+30≥40.


解得m≥5,又m<7,∴5≤m<7.


12.答案为：y=-(x-5)2+3


解析：过点A作AC⊥OB,交OB于点C,


∵AB=6 m,OB=8 m,α=60°,


∴∠BAC=30°,∴BC=AB=3 m,∴OC=OB-BC=5 m,


由勾股定理可得AC=3 m,故可得点A的坐标为(5,3).


设抛物线解析式为y=a(x-5)2+3,


又∵抛物线经过原点,∴a(0-5)2+3=0,解得a=-,


故抛物线解析式为y=-(x-5)2+3.





13.答案为：①②③


解析 由题意知,当70≤x≤150时,y=-2x+400,


∵-2<0,∴y随x的增大而减小,


∴当x=150时,y取得最小值,最小值为100,故①正确;


当x=70时,y取得最大值,最大值为260,故②正确;


设销售这种文化衫的月利润为W元,


则W=(x-60)(-2x+400)=-2(x-130)2+9 800,


∵70≤x≤150,


∴当x=70时,W取得最小值,最小值为-2×(70-130)2+9 800=2 600元,故③正确;


当x=130时,W取得最大值,最大值为9 800元,故④错误.


故其中正确的是①②③.