初中数学北师大版九年级上册第一章 特殊平行四边形1 菱形的性质与判定教学设计

这是一份初中数学北师大版九年级上册第一章 特殊平行四边形1 菱形的性质与判定教学设计，共24页。教案主要包含了教学建议，知识导图， ，总结与反思等内容，欢迎下载使用。




第1讲


讲























菱形的性质与判定












































概 述














【教学建议】


菱形这种图形在生活中也比较常见，在教学过程中，结合现实生活中的菱形物体给学生讲解，必能收到事半功倍的效果.


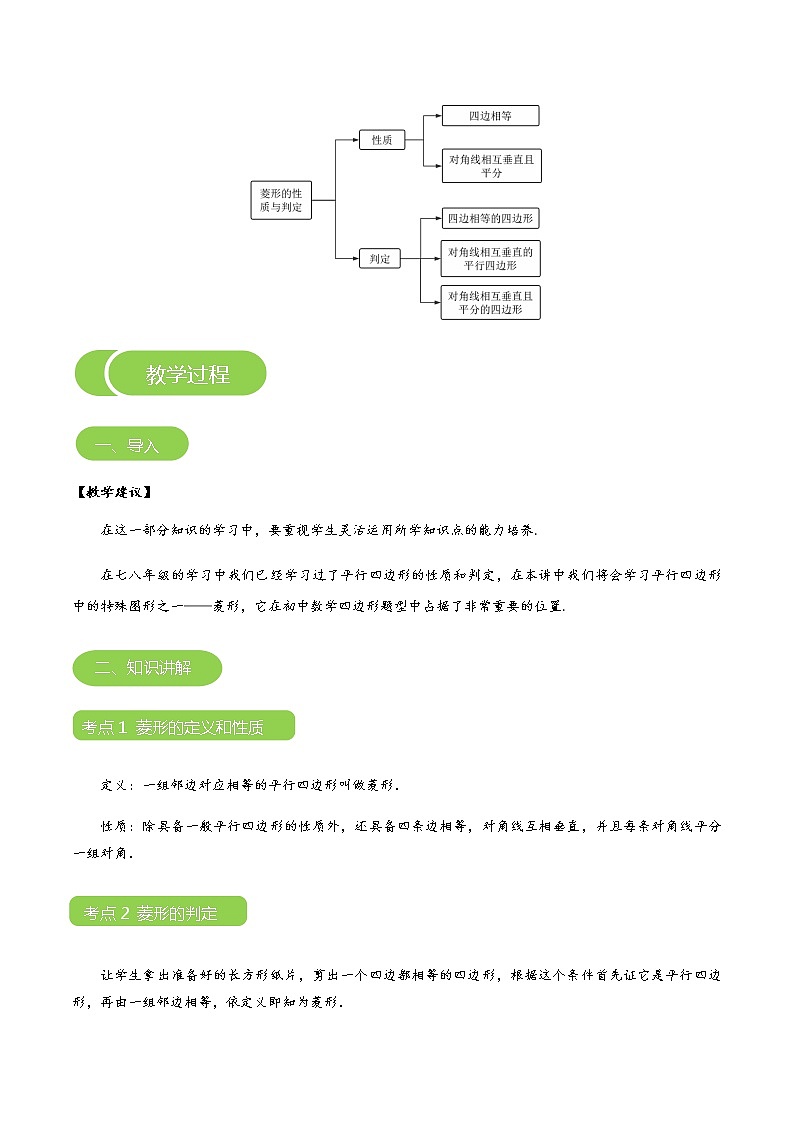
【知识导图】











教学过程








一、导入








【教学建议】


在这一部分知识的学习中，要重视学生灵活运用所学知识点的能力培养.


在七八年级的学习中我们已经学习过了平行四边形的性质和判定，在本讲中我们将会学习平行四边形中的特殊图形之一——菱形，它在初中数学四边形题型中占据了非常重要的位置.





二、知识讲解








考点1 菱形的定义和性质








定义：一组邻边对应相等的平行四边形叫做菱形．


性质：除具备一般平行四边形的性质外，还具备四条边相等，对角线互相垂直，并且每条对角线平分一组对角．


考点2 菱形的判定











让学生拿出准备好的长方形纸片，剪出一个四边都相等的四边形，根据这个条件首先证它是平行四边形，再由一组邻边相等，依定义即知为菱形．


菱形判定定理1：四边都相等的四边形是菱形


1、已知：如图，在 ABCD中，BD⊥AC，O为垂足．


求证：ABCD是菱形.


启发：在已知是平行四边形的情况下，要证明是菱形，只要证明一组邻边相等．


证明：∵四边形ABCD是平行四边形，


∴AO＝CO（平行四边形的对角线互相平分）．


∵BD⊥AC，


∴AD＝CD


∴ABCD是菱形（菱形的定义）．


结论：菱形判定定理2：对角线互相垂直的平行四边形是菱形．


2、猜想：对角线互相垂直平分的四边形是不是菱形？


启发：通过四个直角三角形的全等得到四条边相等．


结论：对角线互相垂直平分的四边形是菱形．





三 、例题精析








类型一 菱形的定义与性质





例题1








如图，菱形ABCD的周长为24cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长等于【 】





A.3cm B.4cm D.2cm


【解析】A.


∵菱形ABCD的周长为24cm，∴边长AB=24÷4=6cm.


∵对角线AC、BD相交于O点，∴BO=DO.


又∵E是AD的中点，∴OE是△ABD的中位线.∴OE=AB=×6=3（cm）.故选A.


【总结与反思】此题运用了菱形的定义与性质：四边相等、对角线相互平分.





类型二 菱形的轴对称性（最值问题）和面积





例题1








如图，已知菱形ABCD中，∠ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD作垂线，垂足分别为E、F．


（1）BD的长是______


（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______．


【解析】 ；．


（1）连接AC，交BD与点O，


∵四边形ABCD是菱形，∠ABC=60°，


∴△ABC为等边三角形，AC=AB=8，


根据菱形性质得：AO=CO=AC=4，OB=OD，AC⊥BD，


根据勾股定理得：BD=2OB=2×=8；


（2）延长FP交BC于点M，则FM⊥BC．


∵PM=PE，


∴PE+PF=PF+PM=FM，


又∵S菱形ABCD=AC•BD=BC•FM，


∴×8×8=8•FM，即FM=4，


∴要使PE+PF+PC取最小值，只要PC取最小值．


当CP⊥BD，即点P与点O重合时，PE+PF+PC的值最小．


此时PB=BO=DO=BD=4．


故答案为：8；4．


【总结与反思】 此题是对菱形定义和性质的灵活运用，通过菱形性质求出了最值.





类型三 菱形的判定





例题1








如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ABCD为菱形的是（ ）


A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°


．


【解析】A


首先根据平移的性质得出AB平行且等于CD，得出四边形ABCD为平行四边形，根据邻边相等的平行四边形是菱形可得添加条件AB=BC即可即可．


试题解析：∵将△ABC沿BC方向平移得到△DCE，


∴AB平行且等于CD，


∴四边形ABCD为平行四边形，


当AB=BC时，平行四边形ACED是菱形．


故选A．


【总结与反思】先证明四边形是平行四边形，再由邻边相等证明四边形是菱形..








四 、课堂运用








基础








1.在菱形ABCD中，若∠ADC=120°，对角线AC=6，则菱形的周长是（ ）


A．4 B．24 C．8 D．24


2.如图，菱形ABCD中，P为对角线AC上一动点，E,F分别为AB、BC中点，若AC=8，BD=6，则PE+PF的最小值为___________.








答案与解析


1.【答案】C


【解析】试题分析：先根据菱形的性质求得∠BAD=60°，AO=3，即可得到△ABD为等边三角形，根据等边三角形可得AB的长，从而求得结果.


∵菱形ABCD，∠ADC=120°，AC=6，


∴AB=AD，∠BAD=60°，AO=3，∠AOB=90°


∴△ABD为等边三角形，∠BAO=30°，


∴AB=2BO，


∵，解得，


∴菱形的周长是，


故选C.


2.【答案】1、5


【解析】设AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，根据菱形的性质推出N是AD中点，P与O重合，推出PE+PF=NF=AB，根据勾股定理求出AB的长即可．


设AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，


∴PN=PE，


∵四边形ABCD是菱形，


∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，


∵E为AB的中点，


∴N在AD上，且N为AD的中点，


∵AD∥CB，


∴∠ANP=∠CFP，∠NAP=∠FCP，


∵AD=BC，N为AD中点，F为BC中点，


∴AN=CF，


在△ANP和△CFP中


∠ANP=∠CFP，AN=CF，∠NAP=∠CFP，


∴△ANP≌△CFP（ASA），


∴AP=CP，


即P为AC中点，


∵O为AC中点，


∴P、O重合，


即NF过O点，


∵AN∥BF，AN=BF，


∴四边形ANFB是平行四边形，


∴NF=AB，


∵菱形ABCD，AC=8，BD=6，


∴AC⊥BD，OA=4，OB=3，


，


则PE+PF的最小值为5.














巩固








1.如图，在菱形ABCD中，对角线AC、BD相交于点O，AC=12，BD=16，E为AD中点，点P在x轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标（-5,0）和（5,0）.请你写出其余所有符合这个条件的P点坐标 .





2.如图所示，在Rt△ABC中，AD平分∠BAC，交BC于D，CH⊥AB于H，交AD于F，DE⊥AB垂足为E，求证：四边形CFDE是菱形.








答案与解析


1.【答案】（，）和（，）


【解析】由在菱形ABCD中，AC=12，BD=16，E为AD中点，根据菱形的性质与直角三角形的性质，易求得OE的长，然后分别从①当OP= OE时，②当OE=PE时，③当OP=EP时去分析求解即可求得答案．


∵四边形ABCD是菱形，AC=12，BD=16，


∴AC⊥BD，OA=AC=6，OD=BD=8，


∴在Rt△AOD中，


∵E为AD中点，


∴OE=AD=5，


①当OP=OE时，P点坐标（-5，0）和（5，0）；


②当OE=PE时，此时点P与D点重合，即P点坐标为（8，0）；


③如图，当OP=EP时，过点E作EK⊥BD于K，作OE的垂直平分线PF，交OE于点F，交x轴于点P，


∴EK∥OA，


∴EK：OA=ED：AD=1：2，


∴EK=OA=3，


∴


∵∠PFO=∠EKO=90°，∠POF=∠EOK，


∴△POF∽△EOK，


∴OP：OE=OF：OK，


即OP：5=：4，


解得，


∴P点坐标为（，0）．


∴其余所有符合这个条件的P点坐标为：（8，0）或（，0）．


2.【答案】证明：∵AD平分∠BAC，


∴∠1=∠2，


∵在Rt△ABC中，CH⊥AB于H，


∴∠1+∠AFH=90°，∠2+∠4=90°，


∵∠3=∠AFH，∠1=∠2，


∴∠3=∠4，


∴FC=CD，


∵DE⊥AB垂足为E，∠ACD=90°，∠1=∠2，


∴CD=DE，∴FC=DE，


∵CH⊥AB，DE⊥AB，


∴FC∥DE，


∴四边形CFED是平行四边形，


∵FC=CD，


∴四边形CFED是菱形





拔高








1.如图，边长为4的菱形ABCD中，∠DAB=60°，E是AD上的动点（与A，D不重合），F是CD上的动点，且AE+CF=4．


（1）求证：不论点E，F的位置如何变化，△BEF是正三角形；


（2）设AE=x，△BEF的面积是S，求S与x的函数关系式．


2.已知AC是菱形ABCD的对角线，∠BAC=60°，点E是直线BC上的一个动点，连接AE，以AE为边作菱形AEFG，并且使∠EAG=60°，连接CG，当点E在线段BC上时（如图1）易证：AB=CG+CE．当点在E线段BC的延长线上时（如图2），猜想AB、CG、CE之间的关系并证明；当点在E线段CB的延长线上时（如图3），猜想AB、CG、CE之间的关系．








答案与解析


1.【答案】见解析


【解析】（1）证明：连接BD，


∵四边形ABCD是菱形，∠DAB=60°，∠ADC=120°，


∴△ABD是正三角形．


∴∠ABD=∠ADB=60°，AB=BD，


又因AE+CF=4，DF+CF=4，


∴AE=DF，


而∠FDB=∠ADC-∠ADB=60°=∠DAB，


∴△AEB≌△DBF，


∴BE=BF，∠ABE=∠DBF，


∵∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=∠ABD=60°


∴△BEF是正三角形．


（2）解：过E作EG⊥AB于点G，


∵AE=x，∠DAB=60°，


∴EG=x，AG=x，


∴BG=4-x，


∴BE2=EG2+BG2=+=


作FH⊥EB垂足为点H，


S△BEF=BE•FH=BEBE==（）．


2.【答案】见解析


【解析】（1）AB=CG-CE


证明：∵AC是菱形ABCD的对角线且∠BAC=60°，


∴AC=AD．


∵四边形AEFG菱形，


∴∠DAC=∠GAE=60°，


∴∠DAG=∠CAE．





在△ACE和△ADG中





∴△ACE≌△ADG（SAS），


∴CE=DG．


∴AB=CD=CG-DG=CG-CE；


（2）AB=CE-CG．


同理可证△ACG≌△ABE，


∴BE=CG．


∴AB=CB=CE-BE=CE-CG．








五 、课堂小结








本节的重要内容：菱形的性质与判定.


①四边都相等的四边形是菱形；


②在已知是平行四边形的情况下，要证明是菱形，只要证明一组邻边相等；


③对角线互相垂直平分的四边形是菱形．








六 、课后作业











基础








1.如图所示，在菱形ABCD中，对角线AC=10，BD=24，AE⊥BC于E，则AE的长是（ ）


A． D．8





2.如图，四边形ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件 ，


使四边形ABCD成为菱形.（只需添加一个条件即可）





3.如图，在菱形ABCD中，∠B=60°，点E、F分别在边AB、AD上，且AE=DF．


（1）试猜想△ECF的形状，并说明理由．


（2）若AB=10，那么△ECF的周长是否存在最小值？如果存在，请求出来；如果不存在，请说明理由．











答案与解析


1.【答案】A


【解析】根据菱形的性质得出BO、CO的长，在RT△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AE，可得出AE的长度．


∵四边形ABCD是菱形，AC=10，BD=24，


∴CO=AC=5，BO=BD=12，AO⊥BO，


∴，


∵，


，解得，


故选A.


2.【答案】OA=OC（答案不唯一）


【解析】根据菱形的判定，平行的性质，全等三角形的判定和性质，由已知，添加OA=OC或AD=BC或AD//BC或AB=BC等即可判定ABCD成为菱形.


3.【答案】见解析.


【解析】△ECF是等边三角形．


证明：连接AC，


∵∠B=60°，


∴AC=AB=CD，∠D=∠CAE=60°


又∵AE=FD，


∴△CDF≌△CEA（SAS），


∴CE=EF，∠ACE=∠DCF，


而∠DCF+∠FCA=60°，


∴∠ACE+FCA=60°=∠ECF，


∴△ECF是等边三角形．


（2）存在．


很明显当CE⊥AB时长度最小，


此时CE=BCsin∠B=5，


∴最小周长=15．











巩固











1. 如图，在四边形ABCD中，AC=BD=6，E、F、G、H分别是AB、BC、CD、DA的中点，则EG2+FH2= .








2.（2011•福州）已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．


（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；


（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，


①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．


②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．








答案与解析


1.【答案】36.


【解析】如图，连接EF，FG，GH，EH，EG与FH相交于点O.


∵E、H分别是AB、DA的中点，∴EH是△ABD的中位线.


∴EH= BD=3.


同理可得EF=GH= AC=3，FG= BD=3.


∴EH=EF=GH=FG=3.∴四边形EFGH为菱形.


∴EG⊥HF，且垂足为O.∴EG=2OE，FH=2OH.


在Rt△OEH中，根据勾股定理得：OE2+OH2=EH2=9.


等式两边同时乘以4得：4OE2+4OH2=9×4=36.


∴（2OE）2+（2OH）2=36，即EG2+FH2=36.


2.【答案】见解析.


【解析】（1）证明：①∵四边形ABCD是矩形，


∴AD∥BC，


∴∠CAD=∠ACB，∠AEF=∠CFE，


∵EF垂直平分AC，垂足为O，


∴OA=OC，


∴△AOE≌△COF，


∴OE=OF，


∴四边形AFCE为平行四边形，


又∵EF⊥AC，


∴四边形AFCE为菱形，


②设菱形的边长AF=CF=xcm，则BF=（8﹣x）cm，


在Rt△ABF中，AB=4cm，


由勾股定理得42+（8﹣x）2=x2，


解得x=5，


∴AF=5cm．


（2）①显然当P点在AF上时，Q点在CD上，此时A、C、P、Q四点不可能构成平行四边形；


同理P点在AB上时，Q点在DE或CE上，也不能构成平行四边形．


因此只有当P点在BF上、Q点在ED上时，才能构成平行四边形，


∴以A、C、P、Q四点为顶点的四边形是平行四边形时，PC=QA，


∵点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，


∴PC=5t，QA=12﹣4t，


∴5t=12﹣4t，


解得t=，∴以A、C、P、Q四点为顶点的四边形是平行四边形时，t=秒．


②由题意得，以A、C、P、Q四点为顶点的四边形是平行四边形时，点P、Q在互相平行的对应边上．


分三种情况：


i）如图1，当P点在AF上、Q点在CE上时，AP=CQ，即a=12﹣b，得a+b=12；


ii）如图2，当P点在BF上、Q点在DE上时，AQ=CP，即12﹣b=a，得a+b=12；


iii）如图3，当P点在AB上、Q点在CD上时，AP=CQ，即12﹣a=b，得a+b=12．


综上所述，a与b满足的数量关系式是a+b=12（ab≠0）．











拔高








1.在菱形ABCD中，∠ABC=60°，E是对角线AC上一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF.


（1）若E是线段AC的中点，如图1，求证：BE=EF；


（2）若E是线段AC或AC延长线上的任意一点，其它条件不变， 如图2、图3，线段BE、EF有怎样的数量关系，直接写出你的猜想；并选择一种情况给予证明.





2.如图①，在菱形ABCD和菱形BEFG中，点A、B、E在同一条直线上，P是线段DF的中点，连接PG，PC．若


（1）请写出线段PG与PC所满足的关系；并加以证明．


（2）若将图①中的菱形BEFG饶点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，原问题中的其他条件不变，如图②．那么你在（1）中得到的结论是否发生变化？若没变化，直接写出结论，若有变化，写出变化的结果．


（3）若将图①中的菱形BEFG饶点B顺时针旋转任意角度，原问题中的其他条件不变，请猜想（1）中的结论有没有变化？





答案与解析


1.【答案】见解析


【解析】（1）延长GP交DC于H，


∵DC∥GF，


∴∠DHP=∠PGF，∠DPH=∠GPF，


∵DP=PF，


∴△DHP≌△PGF，


∴HD=GF，


∵四边形ABCD和四边形GFEB是菱形，


∴DC=CB，FG=GB，


∴DH=GB


∴DC-DH=CB-GB，


∴CH=CG，


∴△CHG就是等腰三角形且CP是底边上的中线，根据等腰三角形三线合一的特点，


即可得出CP⊥PG；


∴线段PG与PC的位置关系是PG⊥PC；


（2）线段PG与PC的位置关系是PG⊥PC；


证明：如图②，延长GP到H，使PH=PG，


连接CH，CG，DH，


∵P是线段DF的中点，


∴FP=DP，


∵∠GPF=∠HPD，


∴△GFP≌△HDP，


∴GF=HD，∠GFP=∠HDP，


∵,


∴∠ADC=∠ABC=60°，∠GBF=60°，


∵四边形ABCD是菱形，


∴CD=CB，∠ADC=∠ABC=60°，点A、B、F又在一条直线上，


∴∠FBC=120°，


∴∠HDC=∠CBG=60°，


∵四边形BEFG是菱形


∴GF=GB，


∴HD=GB，即在△HDC与△GBC中，





，





∴△HDC≌△GBC（SAS），


∴CH=CG，∠DCH=∠BCG，


∴∠DCH+∠HCB=∠BCG+∠HCB=120°，


即∠HCG=120°


∵CH=CG，PH=PG，


∴PG⊥PC．


（3）将图①中的菱形BEFG饶点B顺时针旋转任意角度，


（1）中的结论没有变化，PG⊥PC．


2.【答案】见解析


【解析】（1）图2：BE=EF.图3.


图2证明如下：过点E作EG∥BC，交AB于点G，





∵四边形ABCD为菱形，∴AB=BC.


又∵∠ABC=60°，∴△ABC是等边三角形.


∴AB=AC，∠ACB=60°.


又∵EG∥BC，∴∠AGE=∠ABC=60°.


又∵∠BAC=60°，∴△AGE是等边三角形.∴AG=AE.∴BG=CE.


又∵CF=AE，∴GE=CF.


又∵∠BGE=∠ECF=120°，∴△BGE≌△ECF（SAS）.∴BE=EF.


（2）图2，过点E作EG∥BC，交AB于点G，





根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形，根据等边三角形的性质得到AB=AC，∠ACB=60°，再求出△AGE是等边三角形，根据等边三角形的性质得到AG=AE，从而可以求出BG=CE，再根据等角的补角相等求出∠BGE=∠ECF=120°，然后利用“边角边”证明△BGE和△ECF 全等，根据全等三角形对应边相等即可得证.


图3，证明思路与方法与图2完全相同， 证明如下：


过点E作EG∥BC交AB延长线于点G，





∵四边形ABCD为菱形，∴AB=BC.


又∵∠ABC=60°，∴△ABC是等边三角形.


∴AB=AC∠ACB=60°.


又∵EG∥BC，∴∠AGE=∠ABC=60°.


又∵∠BAC=60°，∴△AGE是等边三角形.∴AG=AE.∴BG=CE.


又∵CF=AE，∴GE=CF.


又∵∠BGE=∠ECF=60°，∴△BGE≌△ECF（SAS）.∴BE=EF.








七 、教学反思











适用学科
初中数学
适用年级
初三
适用区域
北师版区域
课时时长（分钟）
120
知识点
菱形的性质


菱形的轴对称性（最值问题）和面积


菱形的判定


菱形的性质与判定
教学目标
1、掌握菱形的性质与判定.


2、学会应用菱形的性质解决最值问题.
教学重点
能熟练掌握菱形的性质与判定.
教学难点
菱形综合题.