






北师大版九年级上册1 菱形的性质与判定优质课件ppt
展开1.1.1 菱形的性质与判定
北师大版数学九年级上册
教学目标
1、掌握菱形的的定义,理解菱形与平行四边形的“特殊与一般”的关系。 2、理解并掌握菱形的性质定理; 在证明性质和运用性质解决问题的过程中进一步发展学生的逻辑推理能力。
新知导入
平行四边形有哪些特征?矩形与平行四边形比较有哪些特殊的特征?
平行四边形
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
四个角是直角
对角线相等
新知导入
下面几幅图片中都含有一些平行四边形.观察这些平行四边形,你能发现它们有什么样的共同特征?
通过观察发现这些平行四边形的邻边都相等,这就是本节课要研究的特殊平行四边形——菱形.
新知讲解
平行四边形
观察平行四边形图形的变化,你有什么发现?
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
新知讲解
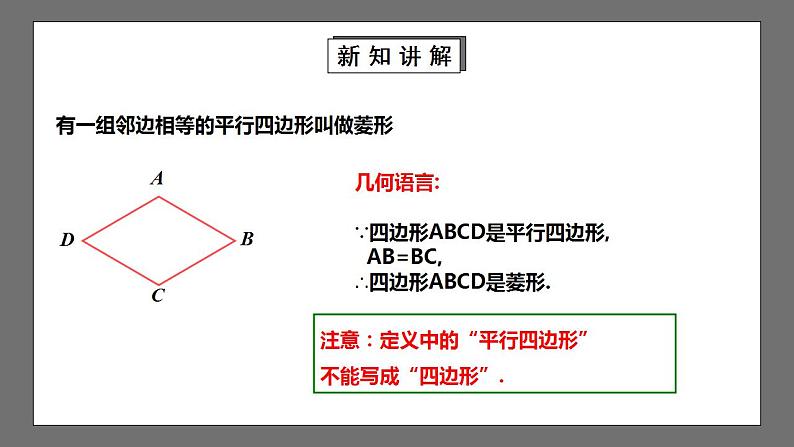
有一组邻边相等的平行四边形叫做菱形
∵四边形ABCD是平行四边形, AB=BC, ∴四边形ABCD是菱形.
几何语言:
注意:定义中的“平行四边形”不能写成“四边形”.
新知讲解
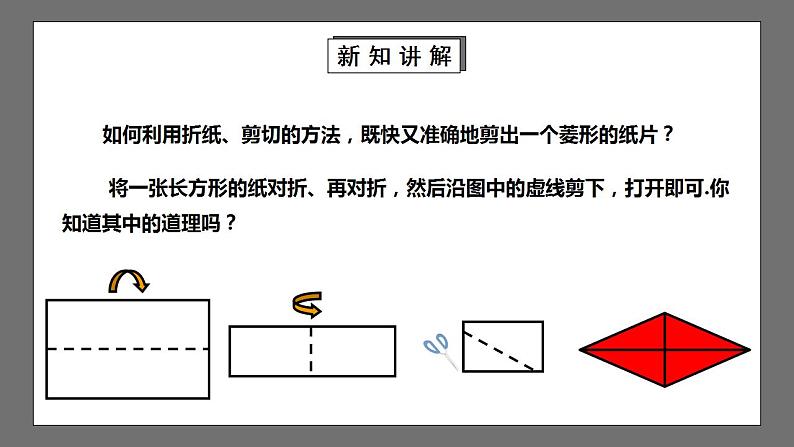
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
新知讲解
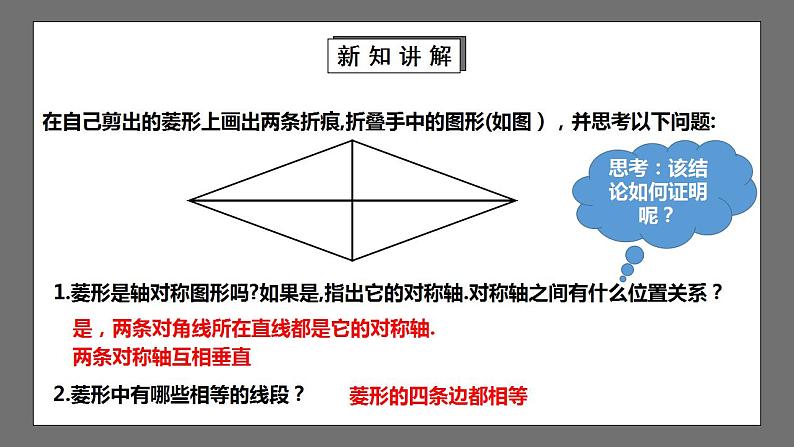
在自己剪出的菱形上画出两条折痕,折叠手中的图形(如图),并思考以下问题:
1.菱形是轴对称图形吗?如果是,指出它的对称轴.对称轴之间有什么位置关系?
2.菱形中有哪些相等的线段?
思考:该结论如何证明呢?
菱形的四条边都相等
是,两条对角线所在直线都是它的对称轴. 两条对称轴互相垂直
新知讲解
中心对称
对边平行且相等
对角相等
对角线互相平分
中心对称轴对称
四条边都相等
对角相等
对角线互相平分且垂直
观察所示的菱形,将你的发现填入下表.
菱形有几条对称轴?
对称中心在哪里?
新知讲解
如图,我们发现,菱形既是中心对称图形,也是轴对称图形,对称轴为它的对角线所在的直线.
由此,很容易猜想菱形所具有的特殊性质:
菱形的四条边都相等.
菱形的对角线互相垂直.
如何证明这两个猜想?
新知讲解
已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.求证明: (1)AB=BC=CD=AD; (2)AC⊥BD.
证明:(1) ∵四边形ABCD是菱形 ∴AB=CD, AD=BC 又∵AB=AD ∴AB=BC=CD=AD
新知讲解
(2)∵AB=AD ∴ △ABD是等腰三角形 又∵四边形ABCD是菱形 ∴OB=OD 在等腰三角形ABD中 ∵OB=OD ∴ AO⊥BD 即AC⊥BD
思考:根据等腰三角形性质,还能推出什么性质?
新知讲解
在等腰三角形ABD中 ∵OB=OD ∴ AO⊥BD ∴ AO平分∠BAD, 即∠DAC=∠BAC. 同理可证∠DCA=∠BCA, ∠ADB=∠CDB,∠ABD=∠CBD.
性质推论:菱形的每一条对角线平分一组对角.
新知讲解
类比平行四边形的性质,从边、角、对角线、对称性四方面有条理的将结论进行归纳.
四条边都相等
对边平行
对角相等
对角线互相垂直
对角线互相平分
每一条对角线平分一组对角
既是中心对称图形又是轴对称图形
新知讲解
例1 如图,在菱形 ABCD 中,对角线 AC 与 BD相交于点 O, ∠BAD = 60°,BD = 6,求菱形的边长 AB 和对角线 AC 的长。
新知讲解
新知讲解
如图,在菱形ABCD中,对角线AC、BD相交于点O, BD=12cm,AC=6cm,求菱形的周长.
新知讲解
菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的面积。
你有什么发现?
新知讲解
菱形的面积公式
菱形的面积 = 底×高 = 对角线乘积的一半
课堂练习
1.如图,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是 ( )A.AB∥DC B.AC=BDC.AC⊥BD D.OA=OC
B
2.若菱形的一条边长为5 cm,则这个菱形的周长为 ( )A.20 cm B.18 cm C.16 cm D.12 cm
A
课堂练习
3、如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .4.如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为 .
(4,4)
课堂练习
5.如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF. 求证:△ABF≌△DAE
证明:∵四边形ABCD是菱形,∴AB=AD,AD∥BC.∴∠BPA=∠DAE.∵∠ABC=∠AED,∴∠BAF=∠ADE.∵∠ABF=∠BPF,∠BPA=∠DAE,∴∠ABF=∠DAE.又∵AB=DA,∴△ABF≌△DAE(ASA).
课堂练习
6.如图,在□ABCD中,对角线AC,BD相交于点O,过点O作MN⊥BD,分别交AD,BC于点M,N.求证:四边形BNDM是菱形.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,OD=OB.∴∠MDO=∠NBO.∵MN⊥BD,∴∠MOD=∠NOB=90°.∴△MOD≌△NOB(ASA).∴MD=NB.又∵ MD∥NB,∴四边形BNDM是平行四边形.又∵MN⊥BD,∴四边形BNDM是菱形.
课堂总结
菱形的判定:
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
板书设计
1.1.1 菱形的性质与判定(1)菱形的定义(2)菱形的性质
作业布置
【必做题】教材第4页随堂练习.【选做题】教材第4页习题1.1的1,2题.
课程结束
北师大版数学九年级上册
数学九年级上册2 视图完美版ppt课件: 这是一份数学九年级上册2 视图完美版ppt课件,文件包含核心素养目标523《视图》课件pptx、核心素养目标523《视图》教案docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
数学2 视图优秀ppt课件: 这是一份数学2 视图优秀ppt课件,文件包含核心素养目标522《视图》课件pptx、核心素养目标522《视图》教案docx等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学北师大版九年级上册2 视图完美版ppt课件: 这是一份初中数学北师大版九年级上册2 视图完美版ppt课件,文件包含核心素养目标521《视图》课件pptx、核心素养目标521《视图》教案docx等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













