

初中北师大版1 菱形的性质与判定教学设计
展开第1讲
讲
菱形的性质与判定
通过对本节课的学习,你能够:
掌握菱形的性质与判定.
学会应用菱形的性质解决最值问题.
.
概 述
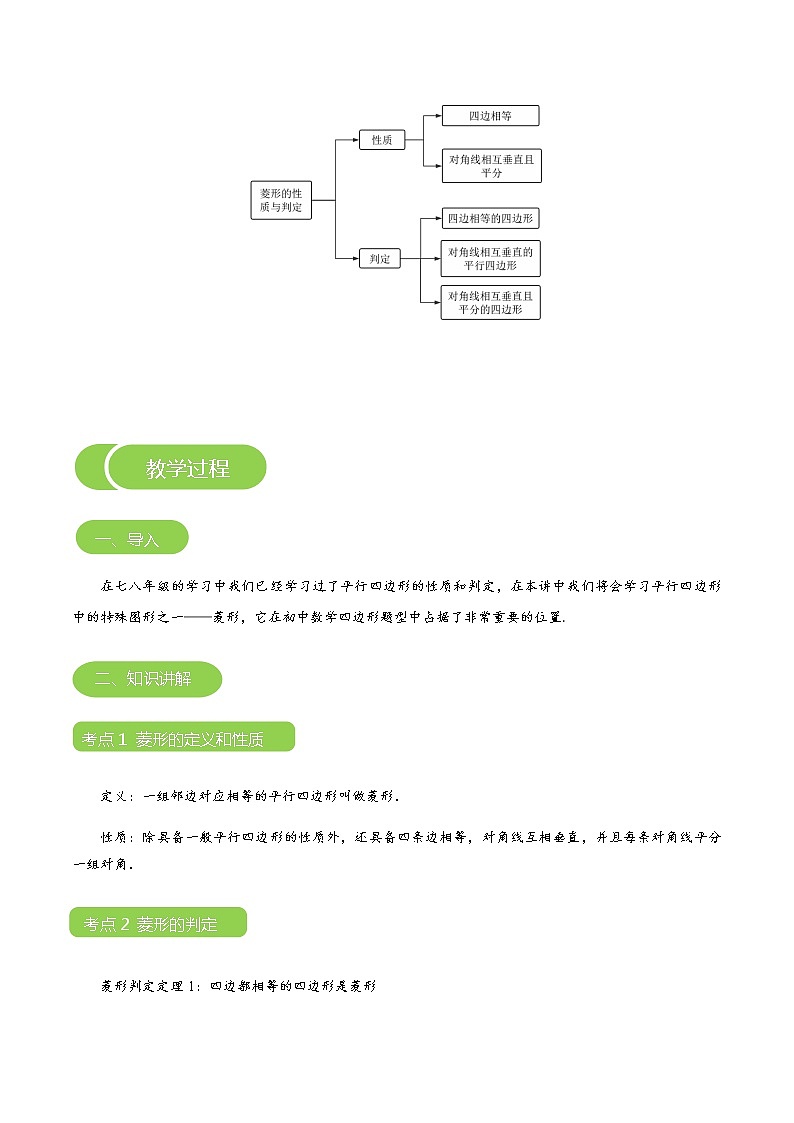
【知识导图】
教学过程
一、导入
在七八年级的学习中我们已经学习过了平行四边形的性质和判定,在本讲中我们将会学习平行四边形中的特殊图形之一——菱形,它在初中数学四边形题型中占据了非常重要的位置.
二、知识讲解
考点1 菱形的定义和性质
定义:一组邻边对应相等的平行四边形叫做菱形.
性质:除具备一般平行四边形的性质外,还具备四条边相等,对角线互相垂直,并且每条对角线平分一组对角.
考点2 菱形的判定
菱形判定定理1:四边都相等的四边形是菱形
1、已知:如图,在 ABCD中,BD⊥AC,O为垂足.
求ABCD是菱形.
启发:在已知是平行四边形的情况下,要证明是菱形,只要证明一组邻边相等.
证明:∵四边形ABCD是平行四边形,
∴AO=CO(平行四边形的对角线互相平分).
∵BD⊥AC,
∴AD=CD
∴ABCD是菱形(菱形的定义).
结论:菱形判定定理2:对角线互相垂直的平行四边形是菱形.
2、猜想:对角线互相垂直平分的四边形是不是菱形?
启发:通过四个直角三角形的全等得到四条边相等.
结论:对角线互相垂直平分的四边形是菱形.
三 、例题精析
类型一 菱形的定义与性质
例题1
如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于【 】
A.3cm B.4cm D.2cm
【总结与反思】
类型二 菱形的轴对称性(最值问题)和面积
例题1
如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD作垂线,垂足分别为E、F.
(1)BD的长是______
(2)连接PC,当PE+PF+PC取得最小值时,此时PB的长是______.
【总结与反思】
类型三 菱形的判定
例题1
如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°
.
【总结与反思】
四 、课堂运用
基础
1.在菱形ABCD中,若∠ADC=120°,对角线AC=6,则菱形的周长是( )
A.4 B.24 C.8 D.24
2.如图,菱形ABCD中,P为对角线AC上一动点,E,F分别为AB、BC中点,若AC=8,BD=6,则PE+PF的最小值为___________.
巩固
1.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(-5,0)和(5,0).请你写出其余所有符合这个条件的P点坐标 .
2.如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFDE是菱形.
.
拔高
1.如图,边长为4的菱形ABCD中,∠DAB=60°,E是AD上的动点(与A,D不重合),F是CD上的动点,且AE+CF=4.
(1)求证:不论点E,F的位置如何变化,△BEF是正三角形;
(2)设AE=x,△BEF的面积是S,求S与x的函数关系式.
2.已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时(如图1)易证:AB=CG+CE.当点在E线段BC的延长线上时(如图2),猜想AB、CG、CE之间的关系并证明;当点在E线段CB的延长线上时(如图3),猜想AB、CG、CE之间的关系.
五 、课堂小结
本节的重要内容:菱形的性质与判定.
①四边都相等的四边形是菱形;
②在已知是平行四边形的情况下,要证明是菱形,只要证明一组邻边相等;
③对角线互相垂直平分的四边形是菱形.
六 、课后作业
基础
1.如图所示,在菱形ABCD中,对角线AC=10,BD=24,AE⊥BC于E,则AE的长是( )
A. D.8
2.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,
使四边形ABCD成为菱形.(只需添加一个条件即可)
3.如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF.
(1)试猜想△ECF的形状,并说明理由.
(2)若AB=10,那么△ECF的周长是否存在最小值?如果存在,请求出来;如果不存在,请说明理由.
巩固
1. 如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2= .
2.(2011•福州)已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
拔高
1.在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)若E是线段AC的中点,如图1,求证:BE=EF;
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变, 如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
2.如图①,在菱形ABCD和菱形BEFG中,点A、B、E在同一条直线上,P是线段DF的中点,连接PG,PC.若
(1)请写出线段PG与PC所满足的关系;并加以证明.
(2)若将图①中的菱形BEFG饶点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变,如图②.那么你在(1)中得到的结论是否发生变化?若没变化,直接写出结论,若有变化,写出变化的结果.
(3)若将图①中的菱形BEFG饶点B顺时针旋转任意角度,原问题中的其他条件不变,请猜想(1)中的结论有没有变化?
适用学科
初中数学
适用年级
初三
适用区域
北师版区域
课时时长(分钟)
120
知识点
菱形的性质
菱形的轴对称性(最值问题)和面积
菱形的判定
菱形的性质与判定
教学目标
1、掌握菱形的性质与判定.
2、学会应用菱形的性质解决最值问题.
教学重点
能熟练掌握菱形的性质与判定.
教学难点
菱形综合题.
初中数学北师大版九年级上册第一章 特殊平行四边形1 菱形的性质与判定教学设计: 这是一份初中数学北师大版九年级上册第一章 特殊平行四边形1 菱形的性质与判定教学设计,共24页。教案主要包含了教学建议,知识导图, ,总结与反思等内容,欢迎下载使用。
数学九年级上册1 反比例函数教案: 这是一份数学九年级上册1 反比例函数教案,共7页。教案主要包含了知识导图,总结与反思等内容,欢迎下载使用。
北师大版九年级上册第五章 投影与视图综合与测试教学设计: 这是一份北师大版九年级上册第五章 投影与视图综合与测试教学设计,共11页。教案主要包含了知识导图,总结与反思等内容,欢迎下载使用。













