初中数学北师大版九年级上册6 利用相似三角形测高教案设计

这是一份初中数学北师大版九年级上册6 利用相似三角形测高教案设计，共15页。教案主要包含了教学建议，知识导图，总结与反思等内容，欢迎下载使用。

第12讲


讲























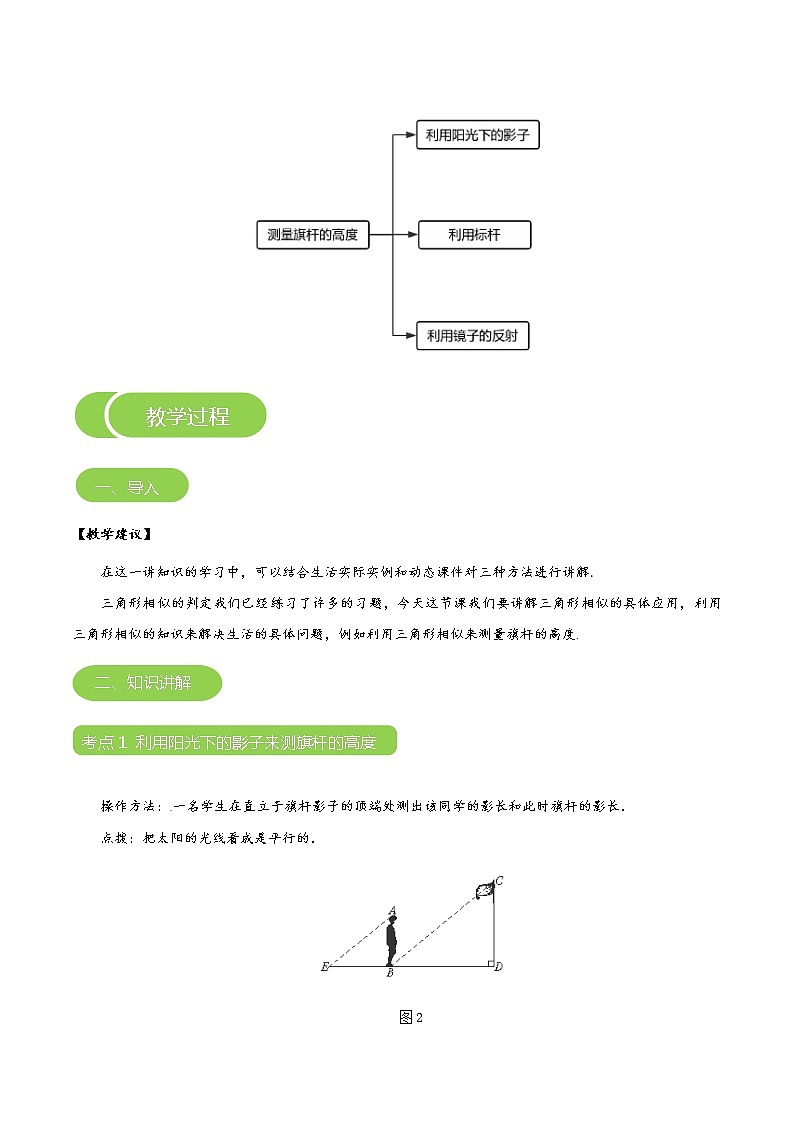
测量旗杆的高度















































概 述











【教学建议】


测量旗杆的高度是三角形相似的重要应用部分，本讲中的三种方法都是热门的考点，因此在学习本讲时，可以采用动态课件与学生共同探讨这三种方法的使用特点，达到理解并应用的目的


【知识导图】











教学过程








一、导入








【教学建议】


在这一讲知识的学习中，可以结合生活实际实例和动态课件对三种方法进行讲解.


三角形相似的判定我们已经练习了许多的习题，今天这节课我们要讲解三角形相似的具体应用，利用三角形相似的知识来解决生活的具体问题，例如利用三角形相似来测量旗杆的高度.





二、知识讲解








考点1 利用阳光下的影子来测旗杆的高度








操作方法：一名学生在直立于旗杆影子的顶端处测出该同学的影长和此时旗杆的影长．


点拨：把太阳的光线看成是平行的．





图2


∵太阳的光线是平行的，∴AE∥CB，∴∠AEB＝∠CBD，


∵人与旗杆是垂直于地面的，∴∠ABE＝∠CDB，∴△ABE∽△CBD ∴ 即CD=[来ZXX因此，只要测量出人的影长BE，旗杆的影长DB，再知道人的身高AB，就可以求出旗杆CD的高度了．[来





考点2 利用标杆来测旗杆的高度








操作方法：选一名学生为观测者，在他和旗杆之间的地面上直立一根高度已知的标杆，观测者前后调整自己的位置，使旗杆顶部、标杆顶部与眼睛恰好在同一直线上时，分别测出他的脚与旗杆底部，以及标杆底部的距离即可求出旗杆的高度．


如图，过点A作AN⊥DC于N，交EF于M．





图3


点拨：∵人、标杆和旗杆都垂直于地面，∴∠ABF＝∠EFD＝∠CDH＝90°


∴人、标杆和旗杆是互相平行的．


∵EF∥CN，∴∠1＝∠2，∵∠3＝∠3，△AME∽△ANC，∴


∵人与标杆的距离、人与旗杆的距离，标杆与人的身高的差EM都已测量出，


∴能求出CN，∵∠ABF＝∠CDF＝∠AND＝90°，∴四边形ABND为矩形．


∴DN＝AB，∴能求出旗杆CD的长度．





考点3 利用镜子反射来测旗杆的高度








操作方法：选一名学生作为观测者．在他与旗杆之间的地面上平放一面镜子，固定镜子的位置，观测者看着镜子来回调整自己的位置，使自己能够通过镜子看到旗杆项端．测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度．


点拨：入射角＝反射角





图4


∵入射角＝反射角 ∴∠AEB＝∠CED ∵人、旗杆都垂直于地面


∴∠B＝∠D＝90°∴


因此，测量出人与镜子的距离BE，旗杆与镜子的距离DE，再知道人的身高AB，就可以求出旗杆CD的高度．





三 、例题精析








类型一 利用影长测高





例题1








同一时刻，身高2.26m的姚明在阳光下影长为1.13m；小林浩在阳光下的影长为0.64m，则小林浩的身高为（ ）


A．1.28m B．1.13mC．0.64mD．0.32m





【解析】A


据相同时刻的物高与影长成比例，


设小林浩的身高为m，


则可列比例式为,


解得，=1.28米．


故选A


【总结与反思】通过利用阳光下的影子所构成的三角形相似即可解答此题..





类型二 利用标杆测高





例题1








九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，求旗杆AB的高度．





【解析】13.5米


∵CD⊥FB，AB⊥FB，∴CD∥AB，


∴△CGE∽△AHE，∴，


即：，∴，


∴AH=11.9，∴AB=AH+HB=AH+EF=11.9+1.6=13.5（m）．





【总结与反思】 此题利用标杆来测量高度.





类型三：利用镜子反射测高





例题1








为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝2.4米，观察者目高CD＝1.6米，则树（AB）的高度为 米．





【解析】5.6米


由题意可知，△DEC∽△BEA，


所以,即，故AB=5.6（米）.


【总结与反思】 通过镜子的反射来测量高度.








四 、课堂运用








基础








1.小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（ ）





A．10米 B．12米 C．15米 D．22.5米





答案与解析


1.【答案】A


【解析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似。因此，


∵，即，∴楼高=10米。故选A。





巩固











1.如图，小明从路灯下向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是_______米．








答案与解析


【答案】5.6


【解析】易得





拔高








1、如图，晚间小明站在距离路灯5m(即BD＝5m)的地面上，发现他的影子长DF为4m．已知小明的身高为1.6m，如果小明再向远离路灯的方向走4m，则此时小明的影长是多少？








答案与解析


1.【答案】影长为7.2m


【解析】先由△FCD∽△FAB得，求得AB的长，再由△GEF∽△GAB，得，可求FG的长，即此时小明的影长．


解：根据题意得，AB∥CD∥EF，BD＝5m，DF＝4m，CD＝EF＝1.6m，所以△FCD∽△FAB，△GEF∽△GAB．由△FCD∽△FAB，得，即，，所以AB＝3.6m．由△GEF∽△GAB，得，即，所以FG＝7.2m，即此时小明的影长为7.2m．











五 、课堂小结








本节的重要内容：利用相似三角形测量旗杆的高度：


1.利用太阳下的影长来测量旗杆的高度


2.利用标杆来测量旗杆的高度


3.利用镜子的反射来测量旗杆的高度








六 、课后作业











基础








1.小明的身高是1.6米，他的影长是2米，同一时刻古塔的影长是18米，则古塔的高是________米．


2.下图中，是木杆和旗杆竖在操场上，其中木杆在阳光下的影子已画出.





（1）用线段表示这一时刻旗杆在阳光下的影子.


（2）比较旗杆与木杆影子的长短.


（3）图中是否出现了相似三角形？


（4）为了出现这样的相似三角形，木杆不可以放在图中的哪些位置？





答案与解析


1.【答案】14.4


【解析】本题主要考查同一时刻物高和影长成正比


利用在同一时刻身高与影长成比例计算．


假设古塔高度为米，则，解得，则古塔的高是14．4米。


2.【答案】见解析


【解析】（1）线段MN即是影长，





（2）旗杆的影子长；


（3）有相似三角形，分别由旗杆及其影子和木杆及其影子以及太阳光线构成；


（4）木杆不可以立在旗杆C影子上.


试题分析：分别作出平行于光线的线，即可得到平行投影，然后根据图形可回答下面的提问．


（1）线段MN即是影长，





（2）旗杆的影子长；


（3）有相似三角形，分别由旗杆及其影子和木杆及其影子以及太阳光线构成；


（4）木杆不可以立在旗杆C影子上.





巩固








1.小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．


9.6米


2米


A


B


C


D








2.如图，为测量学校围墙外直立电线杆AB的高度，小亮在操场上点C处直立高3m的竹竿CD，然后退到点E处，此时恰好看到竹竿顶端D与电线杆顶端B重合；小亮又在点C1处直立高3m的竹竿C1D1，然后退到点E1处，此时恰好看到竹竿顶端D1与电线杆顶端B重合,小亮的眼睛离地面高度EF=1.5m，量得CE=2m，EC1=6m，C1E1=3m。


（1）△FDM∽△ ，△F1D1N∽△ ；


（2）求电线杆AB的高度。





答案与解析


1.【答案】（1）FBG，F1BG（2）15m


【解析】（1）FBG，F1BG。


（2）根据题意，∵D1C1∥BA，∴△F1D1N∽△F1BG。∴。


∵DC∥BA，∴△FDNN∽△FBG。∴。


∵D1N=DM，∴，即。∴GM=16。


∵，∴。∴BG-13.5。


∴AB=BG＋GA=15（m）。


由D1C1∥BA和DC∥BA可得△F1D1N∽△F1BG和△FDNN∽△FBG，根据相似三角形对应边成比例的性质列式求解。


2.【答案】见解析


【解析】作DE⊥AB于点E，





根据题意得：，


，


解得：AE=8米．


则AB=AE+BE=8+2=10米．


即旗杆的高度为10米．


过D点作DN∥BE，得到△CBE∽CDN，△APE∽△ADN.代换即可得出.











拔高








1.如图，甲楼高16米，乙楼坐落在甲楼的正北面，已知当地冬至中午12时，1米长的标杆的影长是米，此时．


(1)如果两楼相距20米，那么甲楼的影子落在乙楼上有多高？


(2)如果甲楼的影子刚好不落在乙楼上，那么两楼的距离是多少？








答案与解析


1.【答案】（1）米．（2）米


【解析】(1)设影长为20米的物体高度为x米，则，


解得，所以．


所以如果两楼相距20米，那么甲楼的影子落在乙楼上的高度为米．


(2)设楼高为16米时，其影长为y米，则，所以．


所以如果甲楼的影子刚好不落在乙楼上，那么两楼的距离为米．


七 、教学反思








适用学科
初中数学
适用年级
初三
适用区域
北师版区域
课时时长（分钟）
120
知识点
利用影长测高


利用标杆测高


利用镜子反射测高


测高综合
教学目标
1、掌握利用相似测高的三种方法.


2、掌握测高的计算.
教学重点
能熟练掌握利用相似测高的方法.
教学难点
能熟练掌握利用相似测高的方法.