北师大版九年级下册4 圆周角和圆心角的关系2课时学案

这是一份北师大版九年级下册4 圆周角和圆心角的关系2课时学案，共4页。学案主要包含了举例，练习等内容，欢迎下载使用。

学习目标:


掌握圆周角定理几个推论的内容,会熟练运用推论解决问题.


学习重点:


圆周角定理几个推论的应用.


学习难点:


理解几个推论的”题设”和”结论”．


学习方法:


指导探索法.


学习过程:


一、举例：


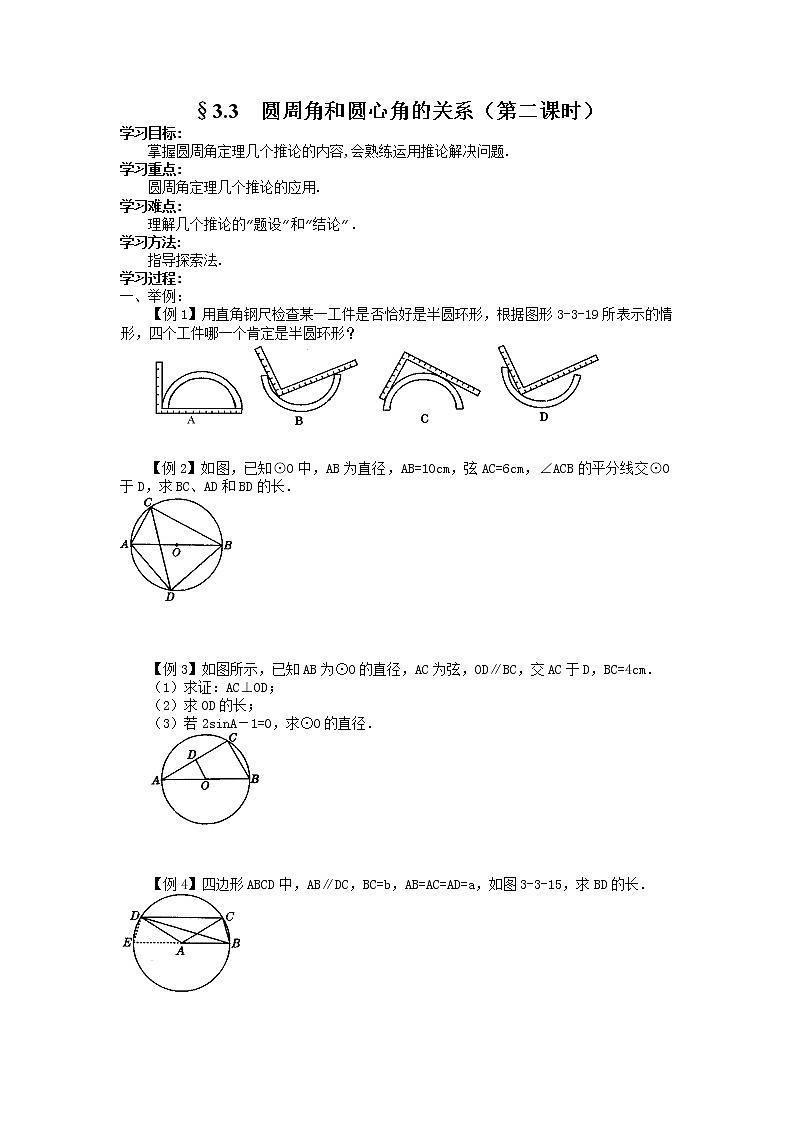
【例1】用直角钢尺检查某一工件是否恰好是半圆环形，根据图形3-3-19所表示的情形，四个工件哪一个肯定是半圆环形？











【例2】如图，已知⊙O中，AB为直径，AB=10cm，弦AC=6cm，∠ACB的平分线交⊙O于D，求BC、AD和BD的长．














【例3】如图所示，已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于D，BC=4cm．


（1）求证：AC⊥OD；


（2）求OD的长；


（3）若2sinA－1=0，求⊙O的直径．














【例4】四边形ABCD中，AB∥DC，BC=b，AB=AC=AD=a，如图3-3-15，求BD的长．














【例5】如图1，AB是半⊙O的直径，过A、B两点作半⊙O的弦，当两弦交点恰好落在半⊙O上C点时，则有AC·AC＋BC·BC=AB2．


（1）如图2，若两弦交于点P在半⊙O内，则AP·AC＋BP·BD=AB2是否成立？请说明理由．


（2）如图3，若两弦AC、BD的延长线交于P点，则AB2=．参照（1）填写相应结论，并证明你填写结论的正确性．





二、练习：


1．在⊙O中，同弦所对的圆周角（ ）


A．相等 B．互补 C．相等或互补 D．都不对


2．如图，在⊙O中，弦AD=弦DC，则图中相等的圆周角的对数是（ ）


A．5对 B．6对 C．7对 D．8对


3．下列说法正确的是（ ）


A．顶点在圆上的角是圆周角


B．两边都和圆相交的角是圆周角


C．圆心角是圆周角的2倍


D．圆周角度数等于它所对圆心角度数的一半


4．下列说法错误的是（ ）


A．等弧所对圆周角相等 B．同弧所对圆周角相等


C．同圆中，相等的圆周角所对弧也相等． D．同圆中，等弦所对的圆周角相等








5．如图4，AB是⊙O的直径，∠AOD是圆心角，∠BCD是圆周角．若∠BCD=25°，则∠AOD=．








6．如图5，⊙O直径MN⊥AB于P，∠BMN=30°，则∠AON=．





7．如图6，AB是⊙O的直径，=，∠A=25°，则∠BOD=．





8．如图7，A、B、C是⊙O上三点，∠BAC的平分线AM交BC于点D，交⊙O于点M．若∠BAC=60°，∠ABC=50°，则∠CBM=，∠AMB=．


9．⊙O中，若弦AB长2cm，弦心距为cm，则此弦所对的圆周角等于 ．





10．如图8，⊙O中，两条弦AB⊥BC，AB=6，BC=8，求⊙O的半径．





11．如图9，AB是⊙O的直径，FB交⊙O于点G，FD⊥AB，垂足为D，FD交AG于E．求证：EF·DE=AE·EG．











12．如图，AB是半圆的直径，AC为弦，OD⊥AB，交AC于点D，垂足为O，⊙O的半径为4，OD=3，求CD的长．





13．如图，⊙O的弦AD⊥BC，垂足为E，∠BAD=∠α，∠CAD=∠β，且sinα=，csβ=，AC=2，求（1）EC的长；（2）AD的长．





14．如图，在圆内接△ABC中，AB=AC，D是BC边上一点．


（1）求证：AB2=AD·AE；


（2）当D为BC延长线上一点时，第（1）小题的结论还成立吗？如果成立，请证明；如果不成立，请说明理由．





15．如图，已知BC为半圆的直径，O为圆心，D是的中点，四边形ABCD对角线AC、BD交于点E．


（1）求证：△ABE∽△DBC；


（2）已知BC=，CD=，求sin∠AEB的值；


（3）在（2）的条件下，求弦AB的长．











16．如图，以△ABC的BC边为直径的半圆交AB于D，交AC于E，过E点作EF⊥BC，垂足为F，且BF：FC=5：1，AB=8，AE=2，求EC的长．