










北师大版九年级下册4 圆周角和圆心角的关系教学ppt课件
展开3.4.1圆周角和圆心角的关系-学案
一、 学习目标
1、理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用;
2、理解圆周角定理的证明中由“特殊到一般”的数学思想方法和完全归纳法的数学思想.
二、温故知新
顶点在圆心的角叫________,圆心角的度数_______它所对弧的度数
三、自主探究:阅读课本p78— 80
探究(一)圆周角的定义
- 观察下列各角, 并说明这些角的共同特征.
如果角的顶点在____________,角的两边____________________________,
像这样的角,叫做圆周角.
2.下列各图中,∠ABC是圆周角吗?
探究(二)圆周角与圆心角的关系
我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系.
1.请在下图中,找出圆周角所对的弧,然后找出这条弧所对的圆心角.
思考:观察上图,圆心O与圆周角的位置关系有哪几种?
2.在上面各图中,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同学交流.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的___________.
探究(三)圆周角定理的推论
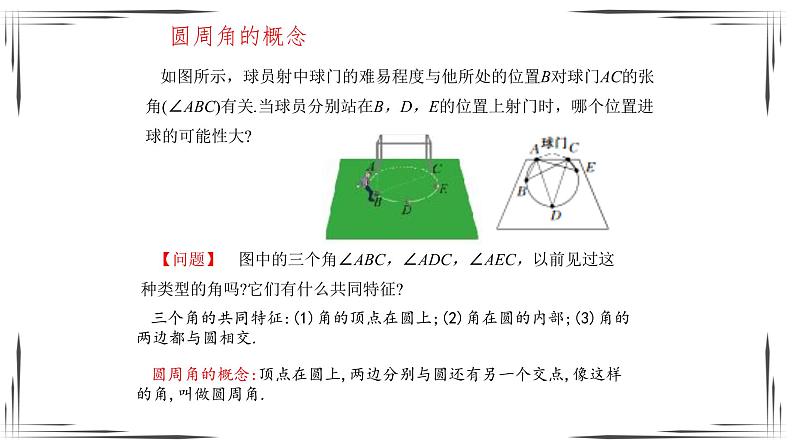
如图:在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角∠ABC有关. 当球员在B、D、E处射门时,他所处的位置对球门所形成的张角
∠ABC、∠ADC、∠AEC,这三个角的大小有什么关系?
归纳:在同圆或等圆中,同弧或等弧所对的圆周角____________.
四、随堂练习
1、看图填空
图(1)中∠ABC= ; 图(2)中,∠BOC= .
(1) (2) (3)
2.如图(3)在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=50°,则∠CAD=_______°.
3. 如图,A、B、C、D是⊙O上的四点,且∠BCD=100°,则∠BOD(所对的圆心角)的度数为__ __°,∠BAD的度数为_ _°.
4.如图,哪个角与∠BAC相等?你能找到几组相等的角?
(3) (4) (5)
5. 如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
五.本课总结:
1.______在圆上,并且角的两边都_________的角叫做圆周角.
- 圆周角定理:在同一圆中,一条弧所对的圆周角等于_______圆心角的_________.
- 圆周角定理的推论:在同圆或等圆中,____________所对的圆周角____________.
你还有什么收获或困惑?
六.当堂检测:
1.如图1,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=( )
A.∠ACD B. ∠ADB C. ∠AED D. ∠ACB
2.如图2,AC是⊙O的直径,弦AB∥CD,若∠BAC=32°,则∠AOD等于( ).
A.64° B.48° C.32° D.76°
3.如图3,弦AB,CD相交于E点,若∠BAC=27°,∠BEC=64°,则∠AOD等于( ).
A.37 B.74° C.54° D.64°
(1) (2) (3) (4)
4.如图4,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=25°,求∠BOC的度数.
答案:
四. 随堂练习
1、40°;60°
2. 25°
3. 160_°, _80_
4.∠BDC; ∠ADB=∠ACB, ∠ABD=∠ACD, ∠DAC=∠DBC
5.证明:∵∠AOB=2∠BOC,∠AOB=2∠ACB ∴∠BOC=∠ACB
∵∠BOC=2∠BAC, ∴∠ACB=2∠BAC
六.当堂检测:
1.A
2.A
3.B.
4.解:∵AB=AD, ∴∠D=∠ABD=25°
∴∠BAC=50°
∴∠BOC=100°
初中数学北师大版九年级下册4 圆周角和圆心角的关系公开课ppt课件: 这是一份初中数学北师大版九年级下册<a href="/sx/tb_c10088_t3/?tag_id=26" target="_blank">4 圆周角和圆心角的关系公开课ppt课件</a>,共25页。PPT课件主要包含了学习目标,情境导入,圆心角的定义,圆周角的定义,探究新知,①角的顶点在圆上,圆周角定理及其推论,议一议,圆心在圆周角的边上,圆心在圆周角内等内容,欢迎下载使用。
浙教版九年级上册3.4 圆心角优秀课件ppt: 这是一份浙教版九年级上册3.4 圆心角优秀课件ppt,文件包含浙教版数学九上341圆心角课件pptx、浙教版数学九上341圆心角教案doc、浙教版数学九上341圆心角学案doc等3份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
2020-2021学年第三章 圆4 圆周角和圆心角的关系教课课件ppt: 这是一份2020-2021学年第三章 圆4 圆周角和圆心角的关系教课课件ppt,文件包含34圆周角和圆心角的关系2-课件ppt、34圆周角和圆心角的关系2-教案doc、34圆周角和圆心角的关系2-练习docx、34圆周角和圆心角的关系2-导学案doc等4份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













