初中数学人教版八年级上册第十五章 分式综合与测试优秀单元测试课后作业题

这是一份初中数学人教版八年级上册第十五章 分式综合与测试优秀单元测试课后作业题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题


1．若分式eq \f(x2－1,x－1)的值为零，则x的值为( )


A．0 B．1 C．－1 D．±1


2．下列式子计算错误的是( )


A.eq \f(0.2a＋b,0.7a－b)=eq \f(2a＋b,7a－b) B.eq \f(x3y2,x2y3)=eq \f(x,y) C.eq \f(a－b,b－a)=－1 D.eq \f(1,c)＋eq \f(2,c)=eq \f(3,c)


3．人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为( )


A．77×10－5 B．0.77×10－7 C．7.7×10－6 D．7.7×10－7


4．化简eq \f(a＋1,a2－2a＋1)÷eq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(2,a－1)))的结果是( )


A.eq \f(1,a2－1) B.eq \f(1,a＋1) C.eq \f(1,a－1) D.eq \f(1,a2＋1)


5．速录员小明打2500个字和小刚打3000个字所用的时间相同，已知小刚每分钟比小明多打50个字，求两人的打字速度．设小刚每分钟打x个字，根据题意列方程，正确的是( )


A.eq \f(2500,x)=eq \f(3000,x－50) B.eq \f(2500,x)=eq \f(3000,x＋50) C.eq \f(2500,x－50)=eq \f(3000,x) D.eq \f(2500,x＋50)=eq \f(3000,x)


6．若关于x的方程eq \f(x＋m,x－3)＋eq \f(3m,3－x)=3的解为正数，则m的取值范围是( )


A．m－eq \f(9,4) D．m>－eq \f(9,4)且m≠－eq \f(3,4)


二、填空题


7．若分式eq \f(3x,x－2)有意义，则x应满足的条件是________．


8．方程eq \f(1,2x)=eq \f(1,x＋1)的解是________．


9．若3x－1=eq \f(1,27)，则x=________.


10．已知a2－6a＋9与(b－1)2互为相反数，则式子eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a,b)－\f(b,a)))÷(a＋b)的值是________．


11．关于x的方程eq \f(2a,x－1)=a－1无解，则a的值是________．


12．若eq \f(1,（2n－1）（2n＋1）)=eq \f(a,2n－1)＋eq \f(b,2n＋1)，对任意自然数n都成立，则a=_______，b=_______；


计算：m=eq \f(1,1×3)＋eq \f(1,3×5)＋eq \f(1,5×7)＋…＋eq \f(1,19×21)=________.





三、解答题


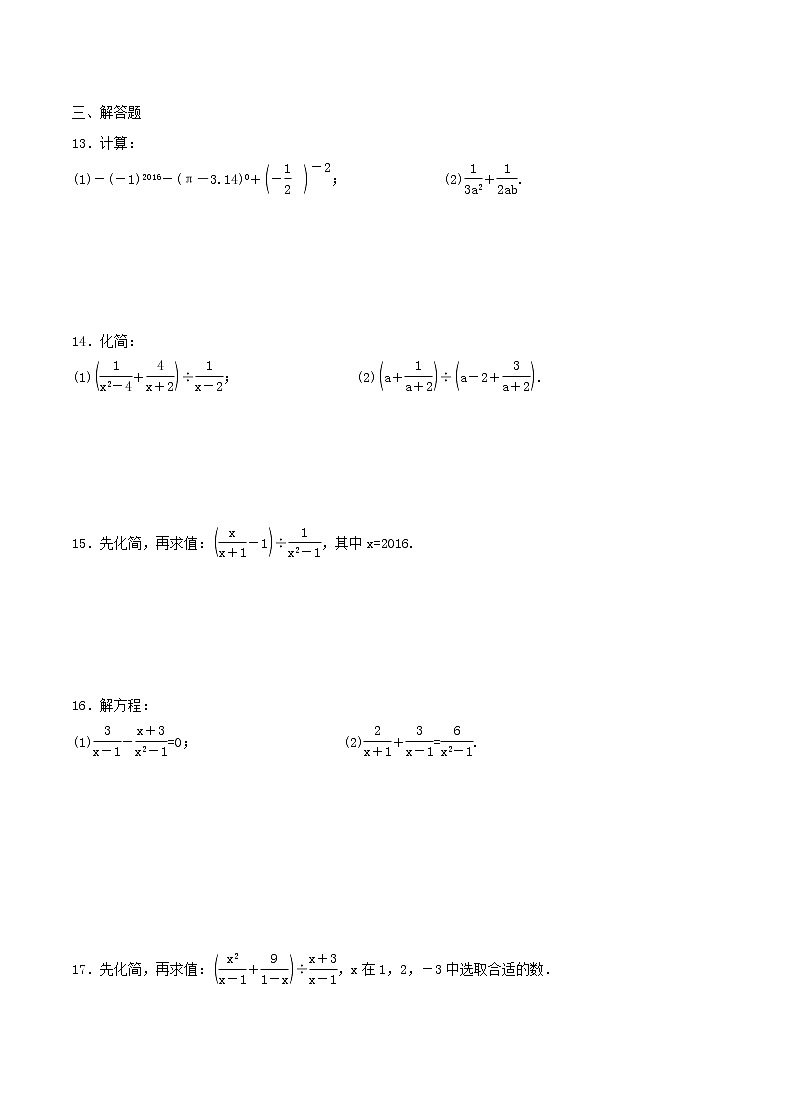
13．计算：


(1)－(－1)2016－(π－3.14)0＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))eq \s\up12(－2)； (2)eq \f(1,3a2)＋eq \f(1,2ab).














14．化简：


(1)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x2－4)＋\f(4,x＋2)))÷eq \f(1,x－2)； (2)eq \b\lc\(\rc\)(\a\vs4\al\c1(a＋\f(1,a＋2)))÷eq \b\lc\(\rc\)(\a\vs4\al\c1(a－2＋\f(3,a＋2))).














15．先化简，再求值：eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,x＋1)－1))÷eq \f(1,x2－1)，其中x=2016.














16．解方程：


(1)eq \f(3,x－1)－eq \f(x＋3,x2－1)=0； (2)eq \f(2,x＋1)＋eq \f(3,x－1)=eq \f(6,x2－1).




















17．先化简，再求值：eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x2,x－1)＋\f(9,1－x)))÷eq \f(x＋3,x－1)，x在1，2，－3中选取合适的数．




















18．先化简，再求值：eq \f(x2＋2x＋1,x＋2)÷eq \f(x2－1,x－1)－eq \f(x,x＋2)，其中x是不等式组eq \b\lc\{(\a\vs4\al\c1(2－（x－1）≥2x，,\f(2x－5,3)－x≤－1))的整数解．




















19．以下是小明同学解方程eq \f(1－x,x－3)=eq \f(1,3－x)－2的过程．


解：方程两边同时乘(x－3)，得


1－x=－1－2. …………………………第一步


解得x=4. ……………………………………第二步


检验：当x=4时，x－3=4－3=1≠0. ………第三步


所以，原分式方程的解为x=4. …………………第四步


(1)小明的解法从第________步开始出现错误；


(2)写出解方程eq \f(1－x,x－3)=eq \f(1,3－x)－2的正确过程．

















20．某中学组织学生到离学校15km的东山游玩，先遣队与大队同时出发，先遣队的速度是大队的速度的1.2倍，结果先遣队比大队早到0.5h，先遣队的速度是多少？大队的速度是多少？























21．老师在黑板上书写了一个代数式的正确演算结果，随后用手掌捂住了一部分，形式如下：





(1)求所捂部分化简后的结果；


(2)原代数式的值能等于－1吗？为什么？















































22．列方程解应用题：


老舍先生曾说“天堂是什么样子，我不晓得，但从我的生活经验去判断，北平之秋便是天堂．”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少．小宇家附近新修了一段公路，他想给市政写信，建议在路的两边种上银杏树．他先让爸爸开车驶过这段公路，发现速度为60千米/时，走了约3分钟．





(1)由此估算这段路长约________千米；


(2)然后小宇查阅资料，得知银杏为落叶大乔木，成年银杏树树冠直径可达8米．小宇计划从路的起点开始，每a米种一棵树，绘制出了示意图，考虑到投入资金的限制，他设计了另一种方案，将原计划的a扩大一倍，则路的两侧共计减少400棵树，请你求出a的值．

















23．观察下列方程的特征及其解的特点．


①x＋eq \f(2,x)=－3的解为x1=－1，x2=－2；


②x＋eq \f(6,x)=－5的解为x1=－2，x2=－3；


③x＋eq \f(12,x)=－7的解为x1=－3，x2=－4.


解答下列问题：


(1)请你写出一个符合上述特征的方程：____________，其解为____________；


(2)根据这类方程特征，写出第n个方程：____________________，其解为________________；


(3)请利用(2)的结论，求关于x的方程x＋eq \f(n2＋n,x＋3)=－2(n＋2)(其中n为正整数)的解．

















参考答案


1．C 2.A 3.C 4.C 5.C


6．B 解析：去分母得x＋m－3m=3x－9，整理得2x=－2m＋9，解得x=eq \f(－2m＋9,2).∵关于x的方程eq \f(x＋m,x－3)＋eq \f(3m,3－x)=3的解为正数，∴－2m＋9＞0，解得m＜eq \f(9,2).当x=3时，即eq \f(－2m＋9,2)=3，解得m=eq \f(3,2).故m的取值范围是m＜eq \f(9,2)且m≠eq \f(3,2).故选B.


7．x≠2 8.x=1 9.－2 10.eq \f(2,3) 11.1或0


12.eq \f(1,2) －eq \f(1,2) eq \f(10,21) 解析：eq \f(1,（2n－1）（2n＋1）)=eq \f(a,2n－1)＋eq \f(b,2n＋1)=eq \f(a（2n＋1）＋b（2n－1）,（2n－1）（2n＋1）)=eq \f(2n（a＋b）＋a－b,（2n－1）（2n＋1）)，∴eq \b\lc\{(\a\vs4\al\c1(a＋b＝0，,a－b＝1，))解得eq \b\lc\{(\a\vs4\al\c1(a＝\f(1,2)，,b＝－\f(1,2).))∴eq \f(1,（2n－1）（2n＋1）)=eq \f(\f(1,2),2n－1)＋eq \f(－\f(1,2),2n＋1)=eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2n－1)－\f(1,2n＋1)))，∴m=eq \f(1,1×3)＋eq \f(1,3×5)＋eq \f(1,5×7)＋…＋eq \f(1,19×21)=eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(1－\f(1,3)＋\f(1,3)－\f(1,5)＋\f(1,5)－\f(1,7)＋…＋\f(1,19)－\f(1,21)))=eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(1－\f(1,21)))=eq \f(10,21).


13．解：(1)原式=－1－1＋4=2.(3分)


(2)原式=eq \f(2b,6a2b)＋eq \f(3a,6a2b)=eq \f(3a＋2b,6a2b).(6分)


14．解：(1)原式=eq \f(1＋4（x－2）,（x＋2）（x－2）)·(x－2)=eq \f(4x－7,x＋2).(3分)


(2)原式=eq \f(a2＋2a＋1,a＋2)÷eq \f(a2－4＋3,a＋2)=eq \f(（a＋1）2,a＋2)·eq \f(a＋2,（a＋1）（a－1）)=eq \f(a＋1,a－1).(6分)


15．解：原式=eq \f(x－x－1,x＋1)·(x2－1)=－(x－1)=－x＋1.(3分)


当x=2016时，原式=－2015.(6分)


16．解：(1)方程两边同乘x2－1，得3(x＋1)－(x＋3)=0，解得x=0.(2分)检验：当x=0时，x2－1≠0，∴原分式方程的解为x=0.(3分)


(2)方程两边同乘x2－1，得2(x－1)＋3(x＋1)=6，解得x=1.(5分)检验：当x=1时，x2－1=0，∴x=1不是原分式方程的解，∴原分式方程无解．(6分)


17．解：eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x2,x－1)＋\f(9,1－x)))÷eq \f(x＋3,x－1)=eq \f(x2－9,x－1)·eq \f(x－1,x＋3)=eq \f(（x＋3）（x－3）,x－1)·eq \f(x－1,x＋3)=x－3.(3分)∵当x=1和x=－3时，原分式无意义，∴选取x=2.当x=2时，原式=2－3=－1.(6分)


18．解：原式=eq \f(（x＋1）2,x＋2)·eq \f(1,x＋1)－eq \f(x,x＋2)=eq \f(x＋1,x＋2)－eq \f(x,x＋2)=eq \f(1,x＋2).(2分)解不等式组eq \b\lc\{(\a\vs4\al\c1(2－（x－1）≥2x，,\f(2x－5,3)－x≤－1，))得－2≤x≤1.(4分)∵x是整数，∴x=－2，－1，0，1.当x=－2，－1，1时，原分式无意义，故x只能取0.(6分)当x=0时，原式=eq \f(1,2).(8分)


19．解：(1)一(2分)


(2)方程两边同时乘(x－3)，得1－x=－1－2x＋6，解得x=4.(7分)检验：当x=4时，x－3≠0.所以，原分式方程的解为x=4.(8分)


20．解：设大队的速度为xkm/h，则先遣队的速度是1.2xkm/h.(1分)根据题意得eq \f(15,x)=eq \f(15,1.2x)＋0.5，解得x=5.(5分)经检验，x=5是原分式方程的解且符合实际．(6分)1.2x=1.2×5=6.(7分)


答：先遣队的速度是6km/h，大队的速度是5km/h.(8分)


21．解：(1)设所捂部分化简后的结果为A，则A=eq \f(x＋1,x－1)·eq \f(x,x＋1)＋eq \f(x2－1,x2－2x＋1)=eq \f(x,x－1)＋eq \f(x＋1,x－1)=eq \f(x＋x＋1,x－1)=eq \f(2x＋1,x－1).(4分)


(2)原代数式的值不能等于－1.(5分)理由如下：若原代数式的值为－1，则eq \f(x＋1,x－1)=－1，即x＋1=－x＋1，解得x=0.


当x=0时，除式eq \f(x,x＋1)=0，故原代数式的值不能等于－1.(9分)


22．解：(1)3(3分)


(2)由题意可得eq \f(3000,a)－eq \f(3000,2a)=eq \f(1,2)×400.(6分)解方程得a=7.5.经检验，a=7.5满足方程且符合题意．(8分)


答：a的值是7.5.(9分)


23．解：(1)x＋eq \f(20,x)=－9 x1=－4，x2=－5(3分)


(2)x＋eq \f(n2＋n,x)=－(2n＋1) x1=－n，x2=－n－1(6分)


(3)x＋eq \f(n2＋n,x＋3)=－2(n＋2)，x＋3＋eq \f(n2＋n,x＋3)=－2(n＋2)＋3，(x＋3)＋eq \f(n2＋n,x＋3)=－(2n＋1)，由(2)知x＋3=－n或x＋3=－(n＋1)，即x1=－n－3，x2=－n－4.(10分)检验：∵n为正整数，当x1=－n－3时，x＋3=－n≠0；当x2=－n－4时，x＋3=－n－1≠0.∴原分式方程的解是x1=－n－3，x2=－n－4.(12分)