初中数学人教版八年级上册13.2 画轴对称图形综合与测试优秀ppt课件

这是一份初中数学人教版八年级上册13.2 画轴对称图形综合与测试优秀ppt课件，共57页。PPT课件主要包含了画轴对称图形，坐标中的轴对称，猜一猜等内容，欢迎下载使用。

我们前面学习了轴对称图形以及轴对称图形的一些相关的性质.如果有一个图形和一条直线，如何画出这个图形关于这条直线对称的图形呢？这节课我们一起来学习作轴对称图形的方法.
3. 通过画轴对称图形，增强学生学习几何的趣味感.
1. 能够按要求画简单平面图形经过一次对称后的图形.
2. 掌握作轴对称图形的方法.
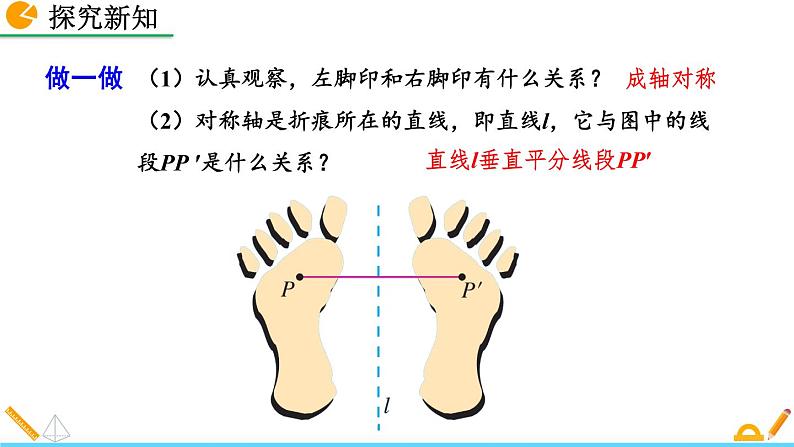
在一张半透明纸的左边部分，画一只左脚印，把这张纸对折后描图，打开对折的纸，就能得到相应的右脚印，这时，右脚印和左脚印成轴对称，折痕所在直线就是它们的对称轴，并且连接任意一对对应点得到的线段被对称轴垂直平分.类似地，请你再画一个图形做一做，看看能否得到同样的结论.
（1）认真观察，左脚印和右脚印有什么关系？
（2）对称轴是折痕所在的直线，即直线l，它与图中的线段PP ′是什么关系？
直线l垂直平分线段PP′
由一个平面图形可以得到与它关于一条直线l对称的图形，这个图形与原图形的形状、大小完全相同；新图形上的每一点都是原图形上的某一点关于直线l的对称点；连接任意一对对应点的线段被对称轴垂直平分.
例1 将一张正方形纸片按如图①，图②所示的方向对折，然后沿图③中的虚线剪裁得到图④，将图④的纸片展开铺平，得到的图案是（ ）
利用轴对称识别图形变化
1.下面是四位同学作的△ABC关于直线MN的轴对称图形，其中正确的是（ ）
例2 如图，将长方形ABCD沿DE折叠，使A点落在BC上的F处，若∠EFB＝50°，则∠CFD的度数为（ ）
A．20° B．30° C．40° D．50°
利用轴对称求角或线段的值
方法点拨：折叠是一种轴对称变换，折叠前后的图形形状和大小不变，对应边和对应角相等．
2．如图，小红把一张含30°角的直角三角形纸片ABC沿较短边的垂直平分线翻折，则∠BOC＝ ．
如何画一个点的轴对称图形？
画出点A关于直线l的对称点A′.
（1）过点A作l的垂线，垂足为点O.
（2）在垂线上截取OA′＝OA.
点A′就是点A关于直线l的对称点.
如何画一条线段的对称图形？
已知线段AB，画出AB关于直线l的对称线段.
【思考】如果有一个图形和一条直线，如何画出与这个图形关于这条直线对称的图形呢？
例3 如图，已知△ABC和直线l，作出与△ABC关于直线l对称的图形.
分析：△ABC可以由三个顶点的位置确定，只要能分别画出这三个顶点关于直线l的对称点，连接这些对称点，就能得到要画的图形.
作法：（1）过点A画直线l的垂线，垂足为点O，在垂线上截取OA′=OA，A′就是点A关于直线l的对称点.
（3）连接A′B′，B′C′，C′A′，得到△ A′B′C′即为所求.
（2）同理，分别画出点B，C关于直线l的对称点B′，C′ .
几何图形都可以看作由点组成.对于某些图形，只要作出图形中一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形.
例4 在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在下面给出的图中画出4个这样的△DEF.
作一个图形关于一条已知直线的对称图形，关键是作出图形上一些点关于这条直线的对称点，然后再根据已知图形将这些点连接起来．
3.如何画线段AB关于直线l 的对称线段A′B′?
作法：1.过点A作直线l的垂线，垂足为点O，在垂线上截OA=O A′ ，点A′就是点A关于直线l的对称点；2.类似地，作出点B关于直线l的对称点B′；3.连接A′B′.
∴ 线段A ′ B ′即为所求.
如图，矩形纸片ABCD中，AB=6cm，BC=8cm．现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（ ）A．6cm B．4cmC．3cm D．2cm
1.作已知点关于某直线的对称点的第一步是（　　）A．过已知点作一条直线与已知直线相交 B．过已知点作一条直线与已知直线垂直 C．过已知点作一条直线与已知直线平行 D．不确定
2.如图，把一张长方形的纸按图那样折叠后，B，D两点落在B′，D′点处，若得∠AOB′=70°，则∠B′OG的度数为________.
3.如图，把下列图形补成关于直线l的对称图形.
如图给出了一个图案的一半，虚线 l 是这个图案的对称轴.整个图案是个什么形状？请准确地画出它的另一半.
如图，画△ABC关于直线m的对称图形.
对称轴是对称点连接的线段的垂直平分线.
(1)找特殊点；(2)作垂线；(3)截取等长；(4)依次连线.
一位外国游客在天安门广场询问小明西直门的位置，但他只知道东直门的位置，聪明的小明想了想，就准确地告诉了他，你能猜到小明是怎么做的吗？
如图，是一幅老北京城的示意图，其中西直门和东直门是关于中轴线对称的.如果以天安门为原点，分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标，你能说出西直门的坐标吗？
1. 理解在平面直角坐标系中，已知点关于x 轴或y 轴对称的点的坐标的变化规律．
2.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法．
平面直角坐标系中的轴对称
已知点A和一条直线MN，你能画出这个点关于已知直线的对称点吗?
∴A′就是点A关于直线MN的对称点.
（2）延长AO至A′,使OA′=AO.
（1）过点A作AO⊥MN，垂足为点O.
如图，在平面直角坐标系中你能画出点A关于x轴的对称点吗?
在平面直角坐标系中画出下列各点关于x轴的对称点.
( , )
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数. （简称：横同纵反）
1.点P(–5, 6)与点Q关于x轴对称，则点Q的坐标为__________.2.点M(a, –5)与点N(–2, b)关于x轴对称，则a=_____, b =_____.
(– 5 , –6 )
如图，在平面直角坐标系中你能画出点A关于y轴的对称点吗?
在平面直角坐标系中画出下列各点关于y轴的对称点.
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等. （简称：横反纵同）
1.点P(–5, 6)与点Q关于y轴对称，则点Q的坐标为__________.2.点M(a, –5)与点N(–2, b)关于y轴对称，则a=_____, b =_____.
例1 如图，四边形ABCD的四个顶点的坐标分别为A(–5,1),B(–2,1),C(–2,5),D(–5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
在平面直角坐标系内作轴对称图形
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形. (一找二描三连）
1.平面直角坐标系中，△ABC的三个顶点坐标分别为A（0,4），B（2,4），C（3，–1）.（1）试在平面直角坐标系中，标出A、B、C三点；（2）若△ABC与△A'B'C'关于x轴对称，画出△A'B'C'，并写出A'、B'、C'的坐标.
例2 已知点A(2a–b，5＋a)，B(2b–1，–a＋b)．(1)若点A、B关于x轴对称，求a、b的值；(2)若A、B关于y轴对称，求(4a＋b)2016的值．
解：(1)∵点A、B关于x轴对称，∴2a–b＝2b–1，5＋a–a＋b＝0，解得a＝–8，b＝–5； (2)∵A、B关于y轴对称，∴2a–b＋2b–1＝0，5＋a＝–a＋b，解得a＝–1，b＝3，∴(4a＋b)2016＝1.
利用轴对称在平面直角坐标系内求字母的值
例3 已知点P(a＋1，2a–1)关于x轴的对称点在第一象限，求a的取值范围．
解：依题意得P点在第四象限，
利用轴对称在平面直角坐标系内求字母的取值范围
方法总结：解决此类题，一般先写出对称点的坐标或判断已知所在的象限，再由各象限内点的坐标的符号，列不等式(组)求解．
5.如图，在平面直角坐标系中，△PQR是△ABC经过某种变换后得到图形，观察点A与点P，点B与点Q，点C与点R的坐标之间的关系，在这种变换下，如果△ABC内任意一点M(a，b)，那么它的对应点N的坐标为 ．
4.已知点M(1–a，2a＋2)，若点M关于x轴的对称点在第三象限，则a的取值范围是 ．
1.如图，点A的坐标（–1，2），点A关于y轴的对称点的坐标为（ ） A．（1，2） B．（–1，–2） C．（1，–2） D．（2，–1）
2.在平面直角坐标系中，点B的坐标是（4，–1），点A与点B关于x轴对称，则点A的坐标是（　　） A．（4，1） B．（–1，4） C．（–4，–1） D．（–1，–4）
1.平面直角坐标系内的点A（–1，2）与点B（–1，–2）关于（　　） A．y轴对称 B．x轴对称 C．原点对称 D．直线y=x对称
2.若点A（1+m，1–n）与点B（–3，2）关于y轴对称，则m+n的值是（　　） A．–5 B．–3 C．3 D．1
3.在平面直角坐标系中，将点A（–1，–2）向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为（　　）A．（–3，–2）B．（2，2）C．（–2，2）D．（2，–2）
4.如图，在平面直角坐标系中，点P（–1，2）关于直线x=1的对称点的坐标为（　　）A．（1，2） B．（2，2） C．（3，2） D．（4，2）
5.已知点P(2a+b,–3a)与点P′（8,b+2).若点P与点P′关于x轴对称，则a=_____， b=_______.若点P与点P′关于y轴对称，则a=_____ ，b=_______.
6.若|a–2|+(b–5)2=0，则点P (a，b)关于x轴对称的点的坐标为________.
1. 已知△ABC的三个顶点的坐标分别为A(–3，5),B(– 4，1),C(–1，3)，作出△ABC关于y轴对称的图形.
解：点A(–3,5),B(–4,1),C(–1,3)关于y轴的对称点分别为A′(3,5),B′(4,1),C′(1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的△A′B′C′.
2. 已知点A（2a+b，–4），B（3，a–2b）关于x轴对称，求点C（a，b）在第几象限？
解：∵点A（2a+b，–4），B（3，a–2b）关于x轴对称， ∴2a+b=3，a–2b=4， 解得a=2，b= –1． ∴点C（2，–1）在第四象限．
在平面直角坐标系中，规定把一个正方形先沿着x轴翻折，再向右平移2个单位称为1次变换．如图，已知正方形ABCD的顶点A、B的坐标分别是（–1，–1）、（–3，–1），把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′，求B的对应点B′的坐标.
解：∵正方形ABCD，点A、B的坐标分别是(–1，–1)、(–3，–1)，∴根据题意，得第1次变换后的点B的对应点的坐标为(–3+2，1)，即(–1，1)，第2次变换后的点B的对应点的坐标为(–1+2，–1)，即(1，–1)，第3次变换后的点B的对应点的坐标为(1+2，1)，即(3，1)，第n次变换后的点B的对应点的为：当n为奇数时为(2n–3，1)，当n为偶数时为(2n–3，–1)，∴把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′，则点B的对应点B′的坐标是(11，1)．
关于坐标轴对称的点的坐标特征
在坐标系中作已知图形的对称图形
关于x轴对称，横同纵反；关于y轴对称，横反纵同.
关键要明确点关于x轴、y轴对称点的坐标变化规律，然后正确画出对称点的位置.