初中人教版第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形优秀课件ppt

这是一份初中人教版第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形优秀课件ppt，共60页。PPT课件主要包含了等腰三角形的性质，ABAC，等腰三角形，AB与AC，BD与CD，AD与AD，∠B与∠C，∠BAD与∠CAD，∠ADB与∠ADC，求证∠BC等内容，欢迎下载使用。

看到下面三角形了吗，它有何特点呢？
我们今天来探讨一下等腰三角形的性质.
1. 探索并掌握等腰三角形的两个性质．
2.会运用等腰三角形的概念和性质解决有关问题.
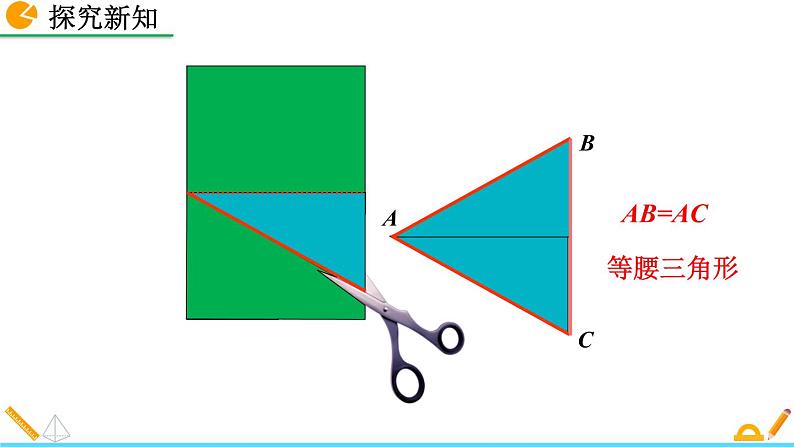
把一张长方形的纸按图中的虚线对折，并剪去阴影部分（一个直角三角形），再把得到的直角三角形展开，得到的三角形ABC有什么特点？
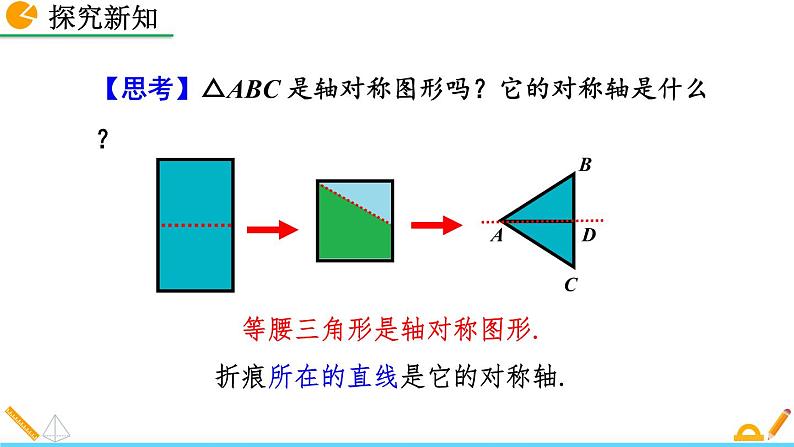
【思考】△ABC 是轴对称图形吗？它的对称轴是什么？
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角.
【思考】由这些重合的角，你能发现等腰三角形的性质吗？说一说你的猜想.
已知：△ABC中，AB=AC,
【思考】如何构造两个全等的三角形？
猜想:等腰三角形的两个底角相等.
如何证明两个角相等呢？
可以运用全等三角形的性质“对应角相等”来证.
已知： 如图，在△ABC中，AB=AC.求证： ∠B= ∠C.
作底边的中线AD， 则BD=CD.
AB=AC ( 已知 )，
BD=CD ( 已作 )，
AD=AD (公共边)，
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一：作底边上的中线.
作顶角的平分线AD，则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
方法二：作顶角的平分线
由△BAD≌ △CAD，除了可以得到∠B= ∠C之外，你还可以得到哪些相等的线段和相等的角？和你的同伴交流一下，看看你有什么新的发现？
解：∵△BAD≌ △CAD，由全等三角形的性质易得BD=CD,∠ADB=∠ADC，∠BAD=∠CAD.又∵ ∠ADB+∠ADC=180°，∴ ∠ADB=∠ADC= 90° ，即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
性质1:等腰三角形的两个底角相等(等边对等角).
如图,在△ABC中, ∵AB=AC(已知),∴∠B=∠C(等边对等角).
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一）.
∵AB=AC, ∠1=∠2(已知)，∴BD=CD, AD⊥BC（等腰三角形三线合一）
∵AB=AC, BD=CD (已知)，∴∠1=∠2, AD⊥BC（等腰三角形三线合一）
∵AB=AC, AD⊥BC(已知)，∴BD=CD, ∠1=∠2（等腰三角形三线合一）
数学语言：如图, 在△ABC中,
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高，看看它们是否重合？
【思考】为什么不一样？
（1）等腰三角形的顶角一定是锐角.（2）等腰三角形的底角可能是锐角，也可能是直角、钝角.（3）钝角三角形不可能是等腰三角形. （4）等腰三角形的顶角平分线一定垂直底边.（5）等腰三角形的角平分线、中线和高互相重合.（6）等腰三角形底边上的中线一定平分顶角.
例1 如图，在△ABC中 ，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.
分析：（1）找出图中所有相等的角；
（2）指出图中有几个等腰三角形？
∠C=∠BDC=∠ABC；
（3）观察∠BDC与∠A、∠ABD的关系，∠ABC、∠C呢？
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A.
（4）设∠A=x ,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠C=180 °，∴ x+2x+2x=180 °,
解：∵AB=AC，BD=BC=AD，∴∠ABC=∠C=∠BDC， ∠A=∠ABD.设∠A=x，则∠BDC= ∠A+ ∠ABD=2x,从而∠ABC=∠C=∠BDC=2x.于是在△ABC中，有 ∠A+∠ABC+∠C=x+2x+2x=180 ° .解得x=36 ° .所以，在△ABC中，∠A=36°，∠ABC=∠C=72°.
在含多个等腰三角形的图形中求角时，常常利用方程思想，通过内角、外角之间的关系进行转化求解.
2.如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数.
解：∵AB=AD=DC ∴ ∠B= ∠ADB，∠C= ∠DAC.设 ∠C=x，则 ∠DAC=x，∠B= ∠ADB= ∠C+ ∠DAC=2x，在△ABC中， 根据三角形内角和定理，得 2x+x+26°+x=180°， 解得x=38.5°.∴ ∠C= x=38.5°， ∠B=2x=77°.
例2 等腰三角形的一个内角是50°，则这个三角形的底角的大小是(　　)A．65°或50° B．80°或40°C．65°或80° D．50°或80°
等腰三角形的分类讨论问题
方法点拨：等腰三角形的两个底角相等，已知一个内角，则这个角可能是底角也可能是顶角，要分两种情况讨论．
3.等腰三角形一个底角为75°,它的另外两个角为_______；4.等腰三角形一个角为70°,它的另外两个角为___________________；5.等腰三角形一个角为110°,它的另外两个角为________.
70°,40°或55°,55°
例3 已知点D、E在△ABC的边BC上，AB＝AC.(1)如图①，若AD＝AE，求证：BD＝CE；(2)如图②，若BD＝CE，F为DE的中点，求证：AF⊥BC.
利用等腰三角形的性质证明线段间的关系
证明：(1)如图①，过A作AG⊥BC于G.∵AB＝AC，AD＝AE，∴BG＝CG，DG＝EG，∴BG–DG＝CG–EG，∴BD＝CE；(2)∵BD＝CE，F为DE的中点，∴BD＋DF＝CE＋EF，∴BF＝CF.∵AB＝AC，∴AF⊥BC.
在等腰三角形有关计算或证明中，有时需要添加辅助线，其顶角平分线、底边上的高、底边上的中线是常见的辅助线．
6. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，∠ABC的平分线BG交AC于点G，交AD于点E，EF⊥AB，垂足为F.(1)若∠BAD＝25°，求∠C的度数；(2)求证：EF＝ED.
1.等腰三角形的一个底角为50°，则它的顶角的度数为_____．
2.如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（　　）A．20°B．35°C．40°D．70°
2.如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=70°，则∠BAC的大小为（　　）A．40° B．30° C．70° D．50°
1.等腰三角形有一个角是90°，则另两个角分别是（ 　）A．30°，60° B．45°，45° C．45°，90° D．20°，70°
3.(1)等腰三角形一个底角为45°,它的另外两个角为_______；(2)等腰三角形一个角为36°,它的另外两个角为____________________；(3)等腰三角形一个角为120°,它的另外两个角为________.
72°,72°或36°,108°
4.在△ABC中， AB=AC，AB的垂直平分线与AC所在的直线相交所得的锐角为50°，则底角的大小为___________．
1.如图，在△ABC中，AB = AC，D是BC边上的中点，∠B = 30°，求 ∠BAD 和 ∠ADC的度数.
解：∵AB=AC，
∴ ∠C= ∠B=30°，∵BD = CD，∴AD⊥BC,∴∠ADB=∠ADC = 90°.
∴∠ BAD =90°– ∠B = 60°.
2.如图，已知△ABC为等腰三角形，BD、CE为底角的平分线，且∠DBC＝∠F，求证：EC∥DF.
∴∠DBC＝∠ECB.∵∠DBC＝∠F，∴∠ECB＝∠F， ∴EC∥DF.
证明：∵△ABC为等腰三角形，AB＝AC，
∴∠ABC＝∠ACB.
又∵BD、CE为底角的平分线， ∴
A、B是4×4网格中的格点，网格中的每个小正方形的边长为1，请在图中标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置．
分别以A、B、C为顶角顶点来分类讨论！
注意是指同一个三角形中.
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上的高和中线与底角的平分线不具有这一性质.
（1）求等腰三角形角的度数时，如果没有明确是底角还是顶角必须分类讨论.（2）等腰三角形“三线合一”定理，角平分线指的是“顶角平分线”.
如图，位于海上B、C两处的两艘救生船接到A处遇险船只的报警，当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发，能不能同时赶到出事地点（不考虑风浪因素）？
1.掌握等腰三角形的判定方法，并运用其进行证明和计算.
2.通过学习等腰三角形的判定方法，使学生能从正反两个方面认识等腰三角形，养成科学的思维习惯.
如图，在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
请同学用直尺和量角器，画一个△ABC，其中∠B=∠C=30°，请你量一量AB与AC的长度，它们之间有什么数量关系，你能得出什么结论？
在△ABD与△ACD，
∴ △ABD ≌ △ACD（AAS）.
过A作AD平分∠BAC交BC于点D.
∴ AC=AB. ( )即△ABC为等腰三角形.
∵∠B=∠C， ( )
等腰三角形的判定方法：
如果一个三角形有两个角相等,那么这两个角所对的边也相等（简写成“等角对等边”，这又是一个判定两条线段相等的根据之一）.
错，因为都不是在同一个三角形中.
【思考】如图,下列推理正确吗?
例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．
已知： 如图，∠CAE是△ABC的外角，∠1=∠2，AD∥BC．
证明：∵AD∥BC，∴∠1=∠B（两直线平行，同位角相等）， ∠2=∠C（两直线平行，内错角相等）． 又∵∠1=∠2， ∴∠B=∠C， ∴AB=AC（等角对等边）．
利用等腰三角形的判定定理判定三角形的形状
1. 已知：如图，AB=DC,BD=CA,BD与CA相交于点E.求证：△AED是等腰三角形.
证明：∵AB=DC，BD=CA，AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边）,
∴ △AED是等腰三角形.
例2 已知：如图，AD∥BC，BD平分∠ABC.求证：AB=AD.
证明：∵ AD∥BC， ∴∠ADB=∠DBC. ∵ BD平分∠ABC， ∴∠ABD=∠DBC， ∴∠ABD=∠ADB， ∴AB=AD.
总结：平分角+平行=等腰三角形
由平行及角平分线识别等腰三角形
2.如图，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于_______.
3.如图，把一张长方形的纸沿着对角线折叠，重合部分是一个等腰三角形吗？为什么？
由折叠可知，∠EBD=∠CBD.
∴∠EDB=∠EBD，∴BE=DE，△EBD是等腰三角形.
∴∠EDB=∠CBD，
例3 如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，AE是∠BAC的平分线，AE与CD交于点F，求证：△CEF是等腰三角形．
证明：∵在△ABC中，∠ACB＝90°，∴∠B＋∠BAC＝90°.∵CD是AB边上的高，∴∠ACD＋∠BAC＝90°，∴∠B＝∠ACD.∵AE是∠BAC的平分线，∴∠BAE＝∠EAC，∴∠B＋∠BAE＝∠ACD＋∠EAC，即∠CEF＝∠CFE，∴CE＝CF，∴△CEF是等腰三角形．
通过计算角相等来证明等腰三角形
“等角对等边”是判定等腰三角形的重要依据，它的前提条件是“在同一个三角形中”．
4.如图所示,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是(　　)　　 　　　　　 　　　　　 A.4B.5C.6D.7
解析: ∵AB=AC，∠ABC=36°，∴∠BAC=108°,∴∠BAD=∠DAE=∠EAC=36°，∴等腰三角形有△ABC,△ABD,△ADE,△ACE,△ACD,△ABE,共有6个.
例4 已知等腰三角形底边长为a,底边上的高的长为h，求作等腰△ABC.使底边BC=a，底边上的高为h.
作法：1.作线段AB=a.2.作线段AB的垂直平分线MN，交AB 于点D.3.在MN上取一点C，使DC=h.4.连接AC，BC，则△ABC即为所求.
利用尺规作图作等腰三角形
例5 如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E，交AC于F.探究EF、BE、FC之间的关系.
解：EF=BE+CF.理由如下：∵ EF∥BC,∴∠EOB=∠CBO，∠FOC=∠BCO. ∵ BO、CO分别平分∠ABC、∠ACB， ∴∠CBO＝∠ABO，∠BCO＝∠ACO，∴∠EOB＝∠ABO ，∠FOC＝∠ACO，∴BE＝OE，CF=OF，∴ EF=EO+FO＝BE+CF.
利用等腰三角形的判定证明线段之间的关系
判定线段之间的数量关系，一般做法是通过证明线段所在的两个三角形全等或利用同一个三角形中“等角对等边”，运用转化思想，解决问题.
5. 在ΔABC中,OB平分∠ABC， OC平分∠ACB，过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗？为什么？
解：∵ OB平分∠ABC，∴∠1=∠2，又 ∵MN∥BC，∴∠2=∠3，∴∠1=∠3∴OM=BM.同理得：ON=CN
在Rt△ABC中，∠ACB=90°，CD⊥AB于D，CE平分∠ACD交AB于E，则下列结论一定成立的是（　　）A．BC=ECB．EC=BEC．BC=BED．AE=EC
解析：∵∠ACB=90°，CD⊥AB，∴∠ACD+∠BCD=90°，∠ACD+∠A=90°，∴∠BCD=∠A．∵CE平分∠ACD，∴∠ACE=∠DCE．又∵∠BEC=∠A+∠ACE，∠BCE=∠BCD+∠DCE，∴∠BEC=∠BCE，∴BC=BE．
1.如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（ ）　A．5个 B．4个 C．3个 D．2个
2.一个三角形的一个外角为130°，且它恰好等于一个不相邻的内角的2倍.这个三角形是（ ）A．钝角三角形 　 B．直角三角形 　C．等腰三角形 　 D．等边三角形
3.如图，直线a、b相交于点O，∠1=50°，点A在直线a上，直线b上存在点B，使以点O、A、B为顶点的三角形是等腰三角形，这样的B点有（　　）A．1个 B．2个 C．3个 D．4个
4.如图，已知∠A=36°，∠DBC=36°，∠C=72°，则∠DBC=_____，∠BDC=_____，图中的等腰三角形有_______________________.
5.如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM＋CN＝9，则线段MN的长为_____.
1.如图，上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°，∠NBC=80°.求从B处到灯塔C的距离.
解：∵∠NBC=∠A+∠C， ∴∠C=80°– 40°= 40°，∴ ∠C = ∠A，∴ BA=BC(等角对等边).∵AB=20×(12–10)=40(海里),∴BC=40海里.答：B处距离灯塔C为40海里.
2.（A类）已知如图，四边形ABCD中，AB=BC，AD=CD，求证：∠A=∠C．（B类）已知如图，四边形ABCD中，AB=BC，∠A=∠C，求证：AD=CD．
证明：（A类）连接AC，∵AB=BC，AD=CD，∴∠BAC=∠BCA，∠DAC=∠DCA，∴∠BAC+∠DAC=∠BCA+∠DCA，即BAD=∠BCD；（B类）连接AC，∵AB=BC，∴∠BAC=∠BCA，又∵∠BAD=∠BCD，即∠BAC+∠DAC=∠BCA+∠DCA，∴∠DAC=∠DCA，∴AD=CD．
在△ABC中，AB=AC，倘若不留神，它的一部分被墨水涂没了，只留下一条底边BC和一个底角∠C，请问，有没有办法把原来的等腰三角形画出来？
3种“补出”方法： 方法1：量出∠C度数，画出∠B＝∠C， ∠B与∠C的边相交得到顶点A． 方法2：作BC边上的垂直平分线，与∠C的一边相交得到顶点A． 方法3：对折．
注意是指同一个三角形中
有两边相等的三角形是等腰三角形