人教版八年级上册13.3.2 等边三角形优质课件ppt

这是一份人教版八年级上册13.3.2 等边三角形优质课件ppt，共60页。PPT课件主要包含了等边三角形的性质，等边对等角，三线合一，等角对等边，两边相等，两腰相等，轴对称图形，等腰三角形，ABAC，∠B∠C等内容，欢迎下载使用。

等边三角形的性质和判定
　　下列图片中有你熟悉的数学图形吗？你能说出此图形的名称吗？
1.掌握等边三角形的定义，等边三角形与等腰三角形的关系.
2.探索等边三角形的性质和判定．
3.能运用等边三角形的性质和判定进行计算和证明．
小明想制作一个三角形的相框，他有四根木条，长度分别为10cm，10cm，10cm，6cm，你能帮他设计出几种形状的三角形？
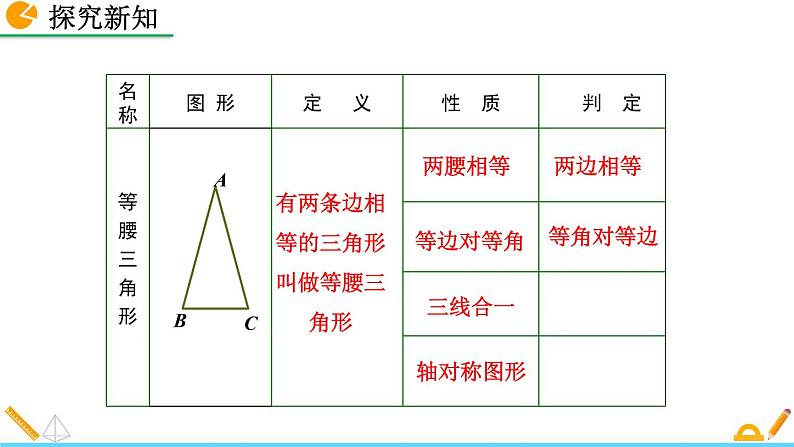
在等腰三角形中，有一种特殊的情况，就是底与腰相等，即三角形的三边相等，我们把三条边都相等的三角形叫做等边三角形.
有两条边相等的三角形叫做等腰三角形
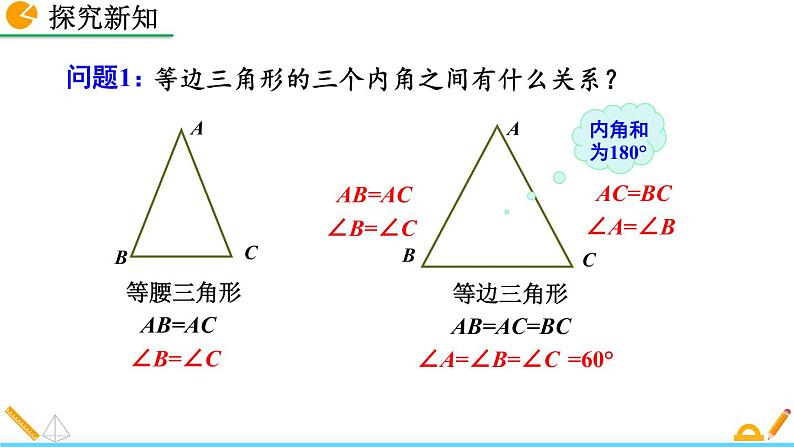
等边三角形的三个内角之间有什么关系？
结论：等边三角形的三个内角都相等，并且每一个角都等于60°.
已知：AB=AC=BC ， 求证：∠A= ∠ B=∠C= 60°.
证明： ∵AB=AC. ∴∠B=∠C .(等边对等角) 同理 ∠A=∠C . ∴∠A=∠B=∠C. ∵ ∠A+∠B+∠C=180°, ∴ ∠A= ∠B= ∠C=60 °.
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴？
结论:等边三角形每条边上的中线、高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高底边的中线三线合一
每条边上的中线、高和这条边所对的角的平分线互相重合
底边上的中线、高和顶角的平分线互相重合
例1 如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE，DE，若∠ABE＝40°，BE＝DE，求∠CED的度数．
解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∵∠ABE＝40°，∴∠EBC＝∠ABC–∠ABE＝60°– 40°＝20°.∵BE＝DE，∴∠D＝∠EBC＝20°，∴∠CED＝∠ACB–∠D＝40°.
解决与等边三角形有关的计算问题，关键是注意“每个内角都是60°”这一隐含条件，一般需结合“等边对等角”、三角形的内角和与外角的性质解答.
1.如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE=CD．求证：BD=DE．
证明：∵△ABC是等边三角形，BD是角平分线，∴∠ABC=∠ACB=60°，∠DBC=30°．又∵CE=CD，∴∠CDE=∠CED．又∵∠BCD=∠CDE+∠CED，∴∠CDE=∠CED=30°．∴∠DBC=∠DEC．∴DB=DE（等角对等边）．
例2 △ABC为等边三角形，点M是BC边上任意一点，点N是CA边上任意一点，且BM＝CN，BN与AM相交于Q点，∠BQM等于多少度？
解：∵△ABC为等边三角形，∴∠ABC＝∠C＝∠BAC＝60°，AB＝BC.又∵BM＝CN，∴△AMB≌△BNC(SAS)，∴∠BAM＝∠CBN，∴∠BQM＝∠ABQ＋∠BAM＝∠ABQ＋∠CBN＝∠ABC＝60°.
此题属于等边三角形与全等三角形的综合运用，一般先利用等边三角形的性质判定三角形全等，而后利用全等及等边三角形的性质，求角度或证明边相等.
2.如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．（1）求证：△ABE≌△CAD；（2）求∠BFD的度数．
（1）证明：∵△ABC为等边三角形，∴∠BAC=∠C=60°，AB=CA，即∠BAE=∠C=60°，在△ABE和△CAD中，∴△ABE≌△CAD（SAS）．（2）解：∵∠BFD=∠ABE+∠BAD，又∵△ABE≌△CAD，∴∠ABE=∠CAD．∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
三个角都相等的三角形是等边三角形
从角看：两个角相等的三角形是等腰三角形
从边看：两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”，你同意吗？
等边三角形的判定方法： 有一个角是60°的等腰三角形是等边三角形.
3.根据条件判断下列三角形是否为等边三角形.
例3 如图，在等边三角形ABC中，DE∥BC，求证：△ADE是等边三角形.
∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
等边三角形的判定的应用
　证明：∵　△ABC 是等边三角形， ∴　∠A =∠ABC =∠ACB =60°． ∵　DE∥BC， ∴　∠ABC =∠ADE， ∠ACB =∠AED. ∴　∠A =∠ADE =∠AED. ∴　△ADE 是等边三角形.
若点D、E 在边AB、AC 的延长线上，且 DE∥BC，结论还成立吗？
若点D、E 在边AB、AC 的反向延长线上，且DE∥BC，结论依然成立吗？
证明： ∵　△ABC 是等边三角形，∴　∠BAC =∠B =∠C =60°．∵　DE∥BC，∴　∠B =∠D，∠C =∠E．∴　∠EAD =∠D =∠E．∴　△ADE 是等边三角形．
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
例4 等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试证明你的结论．
解：△APQ为等边三角形．证明如下：∵△ABC为等边三角形，∴AB＝AC.∵BP＝CQ，∠ABP＝∠ACQ， ∴△ABP≌△ACQ(SAS)，∴AP＝AQ，∠BAP＝∠CAQ.∵∠BAC＝∠BAP＋∠PAC＝60°，∴∠PAQ＝∠CAQ＋∠PAC＝60°，∴△APQ是等边三角形．
判定一个三角形是等边三角形有以下方法：一是证明三角形三条边相等；二是证明三角形三个内角相等；三是先证明三角形是等腰三角形，再证明有一个内角等于60°.
证明：∵△ABC为等边三角形，且AD=BE=CF∴AF=BD=CE，∠A=∠B=∠C=60°，∴△ADF≌△BED≌△CFE（SAS），∴DF=ED=EF，∴△DEF是等边三角形．
4. 如图，等边△ABC中，D、E、F分别是各边上的一点，且AD=BE=CF．求证：△DEF是等边三角形．
如图，在等边三角形ABC中，点D是边BC的中点，则∠BAD=______　．
2.如图，等边三角形ABC的三条角平分线交于点O，DE∥BC，则这个图形中的等腰三角形共有（ ）
A. 4个 B. 5个 C. 6个 D. 7个
1.等边三角形的两条高线相交成钝角的度数是（　　）A．105° B．120° C．135° D．150°
3.在等边△ABC中，BD平分∠ABC，BD=BF，则∠CDF的度数是（　　）A．10° B．15° C．20° D．25°
4.如图,△ABC和△ADE都是等边三角形，已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
5.如图，在△ABC中，∠ACB=90°，∠CAB=30°，以AB为边在△ABC外作等边△ABD，E是AB的中点，连接CE并延长交AD于F．求证：△AEF≌△BEC．
证明：∵△ABD是等边三角形，∴∠DAB=60°，∵∠CAB=30°，∠ACB=90°，∴∠EBC=180°–90°–30°=60°，∴∠FAE=∠EBC．∵E为AB的中点，∴AE=BE．又∵ ∠AEF＝∠BEC， ∴△AEF≌△BEC（ASA）．
如图，A、O、D三点共线，△OAB和△OCD是两个全等的等边三角形，求∠AEB的大小.
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线，
∴∠DOB=∠COA=120°
∴ △COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO，
∴∠AEB=∠AOB=60°.
图①、图②中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．(1)如图①，线段AN与线段BM是否相等？请说明理由；(2)如图②，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．
解：(1)AN＝BM.理由：∵△ACM与△CBN都是等边三角形， ∴AC＝MC，CN＝CB， ∠ACM＝∠BCN＝60°. ∴∠ACN＝∠MCB. ∴△ACN≌△MCB(SAS)． ∴AN＝BM.
(2)△CEF是等边三角形．证明：∵∠ACE＝∠FCM=60°， ∴∠ECF=60°. ∵△ACN≌△MCB， ∴∠CAE＝∠CMB. ∵AC＝MC， ∴△ACE≌△MCF(ASA)， ∴CE＝CF. ∴△CEF是等边三角形．
轴对称图形，每条边上都具有“三线合一”性质
有一个角是60°的等腰三角形
2.这个特殊的直角三角形相比一般的直角三角形有什么不同之处，它有什么特殊性质？
1.等边三角形是轴对称图形，若沿着其中一条对称轴折叠，能产生什么特殊图形？
1.探索含30°角的直角三角形的性质．
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.
如图，将两个相同的含30°角的三角尺摆放在一起，你能借助这个图形找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗？
含30°角的直角三角形的性质
将一张等边三角形纸片，沿一边上的高对折，如图所示，你有什么发现？
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
如图，显然，△ADC与△ABC关于AC成轴对称图形，
因此AB=AD, ∠BAD=2×30°=60°，
从而△ABD是一个等边三角形.
证明：延长BC 到D，使BD =AB，连接AD.在△ABC 中，∵　∠C =90°，∠A =30°, ∴　∠B =60°．∴△ABD 是等边三角形．又∵AC⊥BD,
倍长法就是延长得到的线段是原线段的正整数倍，即1倍、2倍……
证明： 在BA上截取BE=BC，连接EC. ∵ ∠B= 60° ，BE=BC. ∴ △BCE是等边三角形， ∴ ∠BEC= 60°，BE=EC. ∵ ∠A= 30°， ∴ ∠ECA=∠BEC–∠A=60°–30° = 30°. ∴ AE=EC， ∴ AE=BE=BC， ∴ AB=AE+BE=2BC.
在证明中，在较长的线段上截取一条线段等于较短的线段就是截半法.
含30°角的直角三角形的性质：
∵　在Rt△ABC 中，∠C =90°，∠A =30°，
例1 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3cm，则AB的长度是(　　)A．3cm B．6cm C．9cm D．12cm
注意：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．
解析：在Rt△ABC中，∵CD是斜边AB上的高，∴∠ADC＝90°，∴∠ACD＝∠B＝30°.在Rt△ACD中，AC＝2AD＝6cm，在Rt△ABC中，AB＝2AC＝12cm.∴AB的长度是12cm.
利用含30°角的直角三角形的性质求线段的值
1. △ABC中，AB=AC，∠C=30°,DA ⊥BA于A，BD=9.6cm，则AD= .
2.如图∠C=90°，D是CA的延长线上的一点，∠BDC=15°，且AD=AB，则BC= AD.
例2 如图，∠AOP＝∠BOP＝15°，PC∥OA交OB于C，PD⊥OA于D，若PC＝3，则PD等于(　　)A．3 B．2 C.1.5 D．1
解析：如图，过点P作PE⊥OB于E，∵PC∥OA，∴∠AOP＝∠CPO，∴∠PCE＝∠BOP＋∠CPO＝∠BOP＋∠AOP＝∠AOB＝30°.又∵PC＝3，∴PE＝1.5.∵∠AOP＝∠BOP，PD⊥OA，∴PD＝PE＝1.5.
含30°角的直角三角形与角平分线、垂直平分线的综合运用时，关键是寻找或作辅助线构造含30°角的直角三角形．
3.如图，在△ABC 中，∠ACB =90°，CD 是高，∠A =30°，AB =4．则BD = .
4.已知:等腰三角形的底角为15 °,腰长为20.求腰上的高.
解:过C作CD⊥BA,交BA的延长线于点D.
∵∠B=∠ACB=15° (已知),∴∠DAC= ∠B+ ∠ACB= 15°+15°=30°，
例3 如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，过点D作DE⊥AB.DE恰好是∠ADB的平分线．CD与DB有怎样的数量关系？请说明理由．
理由如下：∵DE⊥AB，∴∠AED＝∠BED＝90°.
∵DE是∠ADB的平分线，∴∠ADE＝∠BDE.
又∵DE＝DE，∴△AED≌△BED(ASA)，
在Rt△ACD中，∵∠CAD＝30°，
∴AD＝BD，∠DAE＝∠B.
∴∠BAD＝∠CAD＝∠B.
∵∠BAD＋∠CAD＋∠B＝90°，
∴∠B＝∠BAD＝∠CAD＝30°.
含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据，如果问题中出现探究线段倍分关系的结论时，要联想此性质．
5.Rt△ABC 中，∠C =90°，∠B =2∠A，∠B 和∠A 各是多少度？边AB 与BC 之间有什么关系？　　　
证明：∵∠B+∠A =180°– ∠C=90°， ∠B=2∠A， ∴∠B=60°，∠A=30°. ∴ AB=2BC.
例4　如图是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC，DE 垂直于横梁AC，AB =7.4 cm，∠A =30°，立柱BC、DE 有多长？
利用直角三角形的性质解决实际问题
解：∵DE⊥AC,BC ⊥AC, ∠A=30 °，
答：立柱BC的长是3.7m，DE的长是1.85m.
如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB于C，若EC=1，则OF=　．
解：作EH⊥OA于H，∵∠AOE=∠BOE=15°，EC⊥OB，EH⊥OA，∴EH=EC=1，∠AOB=30°，∵EF∥OB，∴∠EFH=∠AOB=30°，∠FEO=∠BOE，∴EF=2EH=2，∠FEO=∠FOE，∴OF=EF=2．
1.如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为( )A．6米 B．9米 C．12米 D．15米
2.某市在旧城绿化改造中，计划在一块如图所示的△ABC空地上种植草皮优化环境，已知∠A＝150°，这种草皮每平方米售价a元，则购买这种草皮至少需要( )A．300a元 B．150a元C．450a元 D．225a元
3.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC = .
4.如图，Rt△ABC中，∠A= 30°，AB+BC=12cm，则AB=______cm.
1.在△ABC中，∠C=90°，∠B=15°，DE是AB的垂直平分线，BE=5，则求AC的长．
解：连接AE，∵DE是AB的垂直平分线，∴BE=AE，∴∠EAB=∠B=15°，∴∠AEC=∠EAB+∠B=30°．∵∠C=90°，
2.在 △ABC中 ，AB=AC，∠BAC=120° ，D是BC的中点，DE⊥AB于E点，求证：BE=3EA.
证明：∵AB=AC，∠BAC=120°， ∴∠B=∠C=30°.∵ D是BC的中点，∴AD⊥BC∴∠ADC=90°，∠BAD=∠DAC=60°.∴AB=2AD.∵DE⊥AB，∴∠AED=90°，∴∠ADE=30°，∴AD=2AE.∴AB=4AE，∴BE=3AE.
如图，已知△ABC是等边三角形，D,E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q, 求证:BP=2PQ.
∴△ADC≌△BEA.
证明：∵△ABC为等边三角形，
∴ AC=BC=AB ,∠C=∠BAC=60°，
∴∠CAD=∠ABE.∵∠BAP+∠CAD=60°，∴∠ABE+∠BAP=60°.∴∠BPQ=60°.又∵ BQ⊥AD，
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
①分清30 °的角所在的直角边.②作辅助线，构造直角三角形.
前提条件：直角三角形中