初中人教版13.2 画轴对称图形综合与测试学案

这是一份初中人教版13.2 画轴对称图形综合与测试学案，文件包含132画轴对称图形讲义学生版doc、132画轴对称图形讲义教师版doc等2份学案配套教学资源，其中学案共20页， 欢迎下载使用。

（1）知识与技能目标：能够按照要求画出简单平面图形经过一次或两次轴对称得到的图形；
（2）过程与方法目标：经历对称的变换的画图、观察、交流等活动理解其基本性质；
（3）情感态度与价值观：通过动手实践体会轴对称在现实生活中的应用，感受数学美，体会画轴对称图形的过程；
教学重难点
教学重点：利用轴对称作图、关于坐标轴对称的点的坐标特点；
教学难点：用坐标表示轴对称；
知识点一：画轴对称图形
1.关于某直线成轴对称的两个图形之间的关系
由一个平面图形可以得到它关于一条直线成轴对称的图形，这个图形与原图形的形状、大小完全相同；
新图形上的每一点，都是原图形上的某一点关于直线的对称点；
连接任意一对对应点的线段都被对称轴垂直平分.
2.画轴对称图形的方法
几何图形都可以看作由点组成，我们只要分别画出这些点关于对称轴的对称点，再连接这些对称点，就可以得到原图形的轴对称图形；对于一些由直线、线段或射线组成的图形，只要画出图形中的一些特殊点（如线段的端点）关于对称轴的对称点，连接这些对称点，就可以得到原图形的轴对称图形.
画轴对称图形的方法简单归纳如下：
找—再原图形上找特殊点（如线段的端点）；
画-画各个特殊点关于对称轴的对称点；
连-依次连接各对称点.
【提醒】
找特殊点对画轴对称图形极为重要，除线段的端点外，线与线的交点也是画图过程中的特殊点.
对称轴上任一点的对称点是它本身.
例1.已知△ABC和直线MN,求作△A’B’C’,使△A’B’C’和△ABC关于直线MN对称.（不要求写作法，只保留作图痕迹）
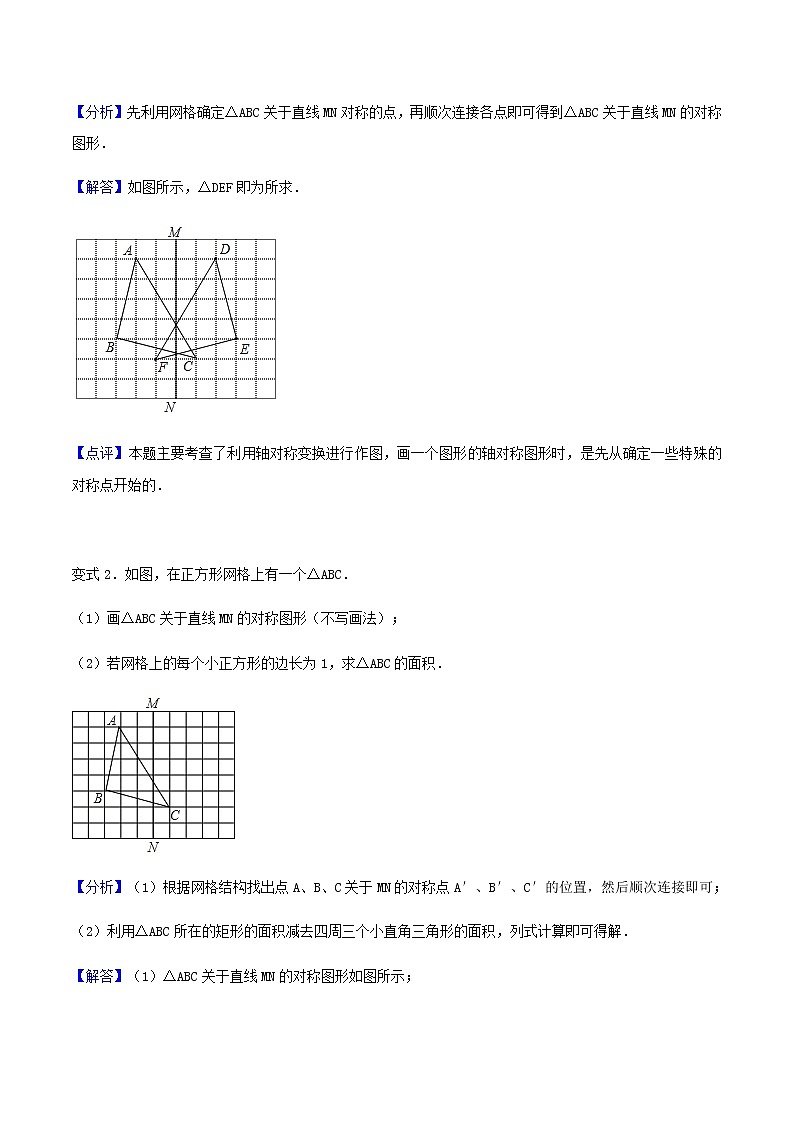
变式1.如图，在正方形网格上有一个△ABC，请画出△ABC关于直线MN的对称图形△DEF（不写画法）．
变式2．如图，在正方形网格上有一个△ABC．
（1）画△ABC关于直线MN的对称图形（不写画法）；
（2）若网格上的每个小正方形的边长为1，求△ABC的面积．
知识点二：关于坐标轴对称的点的坐标特点
点A（x，y）关于x轴对称的点的坐标为（x，-y）；点A（x，y）关于y轴对称的点的坐标为（-x，y）.
【提醒】
横坐标相等，纵坐标互为相反数的两个点关于x轴对称；横坐标互为相反数，纵坐标相等的两个点关于y轴对称，反之也成立.
2.点(a,b)关于直线x=m对称的点的坐标为(2m-a,b),关于直线y=n对称的点的坐标为（a，2n-b).
例1.已知点A坐标为(-1,3)，求：
(1)与点A关于y轴对称的点的坐标；
(2)与点A关于x轴对称的点的坐标.
例2.如图，点A的坐标（﹣1，2），则点A关于y轴的对称点的坐标为（ ）
A．（1，2）B．（﹣1，﹣2）C．（1，﹣2）D．（2，﹣1）

变式1．在平面直角坐标系中，点B的坐标是（4，﹣1），点A与点B关于x轴对称，则点A的坐标是（ ）
A．（4，1）B．（﹣1，4）C．（﹣4，﹣1）D．（﹣1，﹣4）

变式2．若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（ ）
A．﹣5B．﹣3C．3D．1
知识点三：用坐标表示轴对称
在坐标系中画轴对称图形的方法：
计算-计算对称点的坐标；
描点-根据对称点的坐标描点；
连接-依次连接所描各点得到轴对称图形.
【提醒】用坐标表示轴对称体现了轴对称在平面直角坐标系中的应用.用坐标表示轴对称是从数形结合的角度探究如何利用这种坐标变化规律，在平面直角坐标系中作出一个图形的轴对称图形，作一个图形关于坐标轴的轴对称图形，关键是找特殊点及其对应点的坐标.
例1.如图，△ABC的顶点都在正方形网格格点上，点A的坐标为（﹣1，4）．将△ABC沿y轴翻折到第一象限，则点C的对应点C′的坐标是（ ）
A．（3，1）B．（﹣3，﹣1）C．（1，﹣3）D．（3，﹣1）

例2．已知△ABC在直角坐标系中的位置如图所示，如果△A′B′C′与△ABC关于y轴对称，则点A的对应点A′的坐标是（ ）
A．（﹣3，2）B．（3，2）C．（﹣3，﹣2）D．（3，﹣2）

变式1．如图在平面直角坐标系中，△ABC各顶点的坐标分别为：A（4，0），B（﹣1，4），C（﹣3，1）
（1）在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称；
（2）写出点A′B′C′的坐标．
拓展点一：画轴对称图形
例1.用两个全等的三角形，可以拼出各种不同的图形，如图①所示，已画出其中一个三角形，请你补画出一个与其全等的三角形，使图形成轴对称.
要画已知图形关于某直线对称的图形，应先确定对称轴.
拓展点二：点的坐标对称规律的应用
例1.已知点P（2a+b，b）与P1（8，﹣2）关于y轴对称，则a+b= ．
例2.已知点A（a，b）和点B（c，d）（d≠0）关于y轴对称，求3a+3c的值．

变式1．在平面直角坐标系中，O为坐标原点，点A的坐标为（2x+y﹣3，x﹣2y），它关于x轴的对称点A1的坐标为（x+3，y﹣4），关于y轴的对称点为A2．
求A1、A2的坐标；
拓展点三：平面直角坐标系中的轴对称作图
例1.如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．
变式1.如图，网格中的每个小正方形的边长均为1个单位长度，Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A（4，3），点B（1，1），点C（4，1）．
（1）画出Rt△ABC关于y轴对称的Rt△A1B1C1，（点A、B、C的对称点分别是A1、B1、C1），直接写出A1的坐标；
（2）将Rt△ABC向下平移4个单位，得到Rt△A2B2C2（点A、B、C的对应点分别是A2、B2、C2），画出Rt△A2B2C2，连接A1C2，直接写出线段A1C2的长．