初中数学人教版七年级上册第一章 有理数1.5 有理数的乘方1.5.1 乘方完美版ppt课件

这是一份初中数学人教版七年级上册第一章 有理数1.5 有理数的乘方1.5.1 乘方完美版ppt课件，共46页。PPT课件主要包含了乘方的意义，分裂方式如下所示，分裂两次呢，分裂三次呢四次呢，例如2×2×2×2，试一试，例1计算，乘方的计算，用计算器计算，–175616等内容，欢迎下载使用。

珠穆朗玛峰是世界最高的山峰，它的海拔高度约是8844米．把一张足够大的厚度为0.1毫米的纸，连续对折30次的厚度能超过珠穆朗玛峰，这是真的吗？
1. 理解并掌握有理数的乘方、幂、底数、指数的概念及意义.
2. 体会有理数乘方运算的符号法则，熟练进行有理数的乘方运算.
某种细胞每30分钟便由一个分裂成两个，经过3小时这种细胞由1个能分裂成多少个？
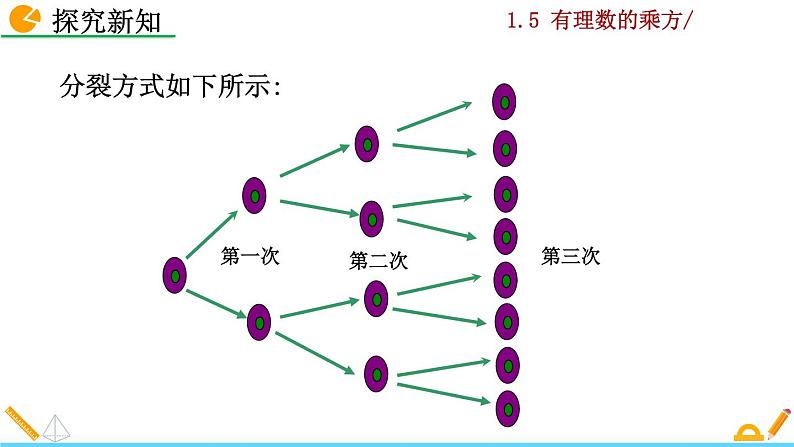
这个细胞分裂一次可得多少个细胞?
那么，3小时共分裂了多少次?有多少个细胞？
解: 一次： 两次： 三次： 四次：
六次: 2×2×2×2×2×2个.
请比较细胞分裂四次后的个数式子:2×2×2×2和细胞分裂六次后的个数式子: 2×2×2×2×2×2. 这两个式子有什么相同点?
它们都是乘法，并且它们各自的因数都相同.
【想一想】这样的运算能像平方、立方那样简写吗？
一般地，n个相同的因数a相乘，记作an，读作“a的n次幂（或a的n次方）”，即
2×2×2×2×2×2
读作2的6次方(幂).
读作2的4次方(幂).
这种求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂.
一个数可以看作这个数本身的一次方，例如，8就是81，指数1通常省略不写. 因为an就是n个a相乘，所以可以利用有理数的乘法运算来进行有理数的乘方运算.
1. (–5)2的底数是_____，指数是_____，(–5)2表示2个_____相乘，读作_____的2次方，也读作–5的_____.2. 表示 个 相乘，读作 的 次方，也读作 的 次幂，其中 叫做 ，6叫做 .
温馨提示：幂的底数是分数或负数时，底数应该添上括号！
解：（1）(–4)3=(–4)×(–4)×(–4)=–64；
（2）(–2)4 =(–2)×(–2)×(–2)×(–2)=16；
你发现负数的幂的正负有什么规律？
1.负数的奇次幂是负数，负数的偶次幂是正数.
2.正数的任何正整数次幂都是正数，0的任何正整数次幂都是0.
根据有理数的乘法法则可以得出：
（4）　　　　　　　　　　　　　；( )
1.判断：(对的画“√”，错的画“×”.)
（1） 32 = 3×2 = 6；( )
（2）(–2)3 ＝ (–3)2； ( )
（3） –32 = (–3)2；( )
（5） . ( )
32 = 3×3=9
(–2)3＝–8；(–3)2=9
–32 = –9； (–3)2=9
–24= –2×2×2×2= –16
例2 用计算器计算(–8)5和(–3)6.
所以(–8)5= –32768，(–3)6=729.
利用计算器进行乘方的计算
（1） =_________
（2） =___________
（3） =_________
（4） =__________
2.若运用初中数学教材中使用的某种电子计算器进行计算，则按键的结果为( )A.16 B.33 C.37 D.36
（1）（2）–23×(–32)（3）64÷(–2)5 （4）(–4)3÷(–1)200+2×(–3)4
（2） –23×(–32)= –8×(–9)=72；
（3）64÷(–2)5=64÷(–32)= –2；
（4）(–4)3÷(–1)200+2×(–3)4 = –64÷1+2×81=98
【思考】通过以上计算，对于乘除和乘方的混合运算， 你觉得有怎样的运算顺序？
先算乘方，后算乘除；如果遇到括号，就先进行括号里的运算.
解：（1）原式＝ = 1
（2）原式＝ = 4
（3）原式＝–2×3–36= –42
1.计算(–3)2的等于（　　） A．5 B．–5 C．9 D．–92.计算(–1)2017的结果是（ ） A. –1B. 1C. 2017D. –2017
（1）–(–3)2= ; （2）–32= ;
（3）(–5)3= ; （4）0.13= ;
（5）(–1)9= ; （6）(–1)12= ;
（7）(–1)2n= ; （8）(–1)2n+1= ;
（9）(–1)n= .
（当n为奇数时）（当n为偶数时）
2.计算： .
解：原式= =18-12=6
3.下列说法中正确的是（ ） A. 23表示2×3的积 B. 任何一个有理数的偶次幂是正数 C. -32与(-3)2互为相反数 D.一个数的平方是 ，这个数一定是
2.对任意实数a，下列各式不一定成立的是（ ）
1. 在 中，最大的数是(　　)
厚度是0.1毫米的纸,将它对折1次后,厚度为0.2毫米.
（1）对折3次后,厚度为多少毫米?（2）对折7次后,厚度为多少毫米?（3）用计算器计算对折30次后纸的厚度.
0.1×230=0.1×1073741824=107374182.4（毫米）
107374182.4毫米=107374.1824米
1.求几个相同因数的积的运算，叫做乘方.
（1）正数的任何次幂都是正数.
（2）负数的奇次幂是负数，负数的偶次幂是正数.
（3）零的正整数次幂都是零.
【思考】（1）我们学习了哪些运算？（2）在2+32×(–6)这个式子中，存在着哪些运算？这些运算如何进行呢？
1.掌握有理数的混合运算顺序，能熟练地进行有理数的混合运算.
2.会根据一组数的特点，探究与乘方有关的规律性问题.
圆形花坛的半径为3m，中间雕塑的底面是边长为1 m的正方形
估计每平方米种9株花，我要买几株花呀？
羊村的花坛里的花都快枯萎了，我们重新种上吧！
【思考】上式含有哪几种运算？先算什么？后算什么？
做有理数的混合运算时，应注意以下运算顺序：
1. 先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行.
（1）2×(–3)3–4×(–3)+15; （2）(–2)3+(–3)×[(–4)2+2]–(–3)2÷(–2).
解：（1）原式=2×(–27)–(–12)+15
= –54+12+15
= –8+(–3)×18–(–4.5)
（2）原式= –8+(–3)×(16+2)–9÷(–2)
= –8–54+4.5
解：原式= = =
= – 4 – 36
例2 计算： .
解法一：原式=
点拨：在运算过程中，巧用运算律，可简化计算.
讨论交流：你认为哪种方法更好呢？
= –6+(–5)
2.计算： .
解：原式= = =－9
例3 观察下面三行数： –2， 4， –8， 16， –32， 64，…； ① 0， 6， –6， 18， –30， 66，…； ② –1， 2， –4， 8， –16， 32，…. ③（1）第①行数按什么规律排列？
分析：观察①，发现各数均为2的倍数.联系数的乘方，从符号和绝对值两方面考虑，可发现排列的规律.
（2）第②③行数与第①行数分别有什么关系？
解：（2）第②行数是第①行相应的数加2，即
第③行数是第①行相应的数除以2，即
（3）取每行数的第10个数，计算这三个数的和.
解：（3）每行数中的第10个数的和是：
=1024+1026+512
3.观察下列各式:
1. 计算4+（–2）2×5=（　　） A．–16 B．16 C．20 D．24
解析：4+(–2)2×5=4+4×5=4+20=24.
1.计算式子(–1)3 +(–1)6的结果是（ ） A.1 B.–1 C.0 D.1或–12.设a=–2×32, b=(–2×3)2, c=–(2×3)2，那么a、b、c的大小关系是( ) A.a3. 计算：(-2)2018+(-2)2019.
解：原式=22018 – 22019 = 22018 – 22018×2 = 22018 –22018 –22018　　　　　 = –22018
（1） ；
一个长方体的长、宽都是a，高是b，它的体积和表面积怎样计算？当a=2 cm，b=5 cm时，它的体积和表面积是多少？
解：体积V=a2b=22×5=20 cm3.表面积S=2a2+4ab=2×22+4×2×5=48 cm2.
先乘方，再乘除，最后加减
同级运算，从左到右进行；
如有绝对值，先算绝对值.
有括号的，先做括号内的运算，按先小括号、再中括号、后大括号的顺序依次进行；