初中数学人教版七年级上册1.5.1 乘方教课课件ppt

课题名

《有理数的乘方一》

教学目标

理解有理数乘方的意义，了解幂，乘方，底数，指数等概念。掌握有理数乘方的符号法则以及相关性质，能正确进行有理数乘方的计算。

教学重点

理解有理数乘方的意义，了解幂，乘方，底数，指数等概念。

教学难点

掌握有理数乘方的符号法则以及相关性质，能正确进行有理数乘方的计算。

教学过程

一、课前预热

珠穆朗玛峰是世界最高的山峰，它的海拔高度约是8844米，把一张足够大的厚度为0.1毫米的纸，连读对折30次的厚度能超过珠穆朗玛峰，这时真的吗？

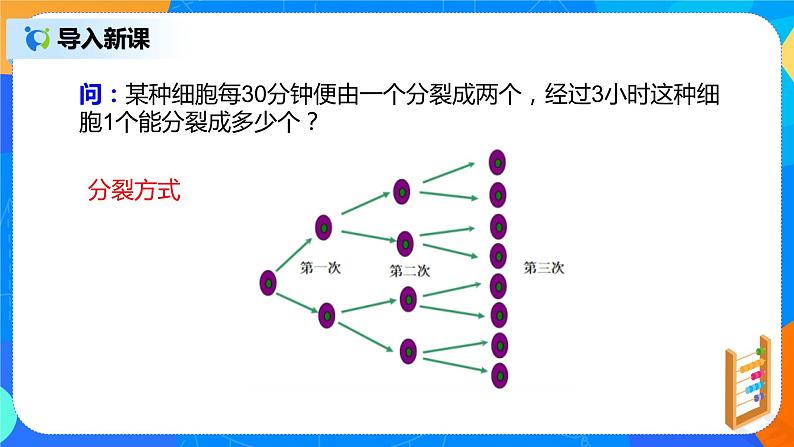
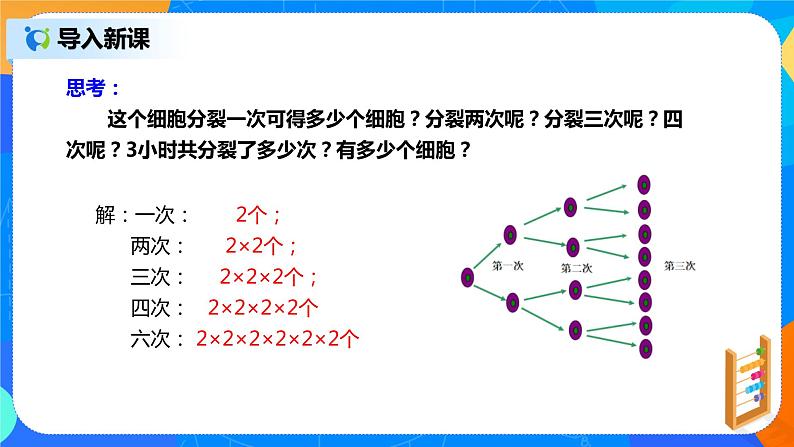
二、导入新课

问：某种细胞每30分钟便由一个分裂成两个，经过3小时这种细胞1个能分裂成多少个？

分裂方式

思考：

       这个细胞分裂一次可得多少个细胞？分裂两次呢？分裂三次呢？四次呢？3小时共分裂了多少次？有多少个细胞？

解：一次：       2个；

      两次：      2×2个；

      三次：     2×2×2个；

      四次：   2×2×2×2个

      六次： 2×2×2×2×2×2个

请比较细胞分裂四次后的个数式子：2×2×2×2和细胞分裂六次后的个数式子：2×2×2×2×2×2。

这两个式子有什么相同点？

它们都是乘法，并且它们各自的因素都相同。

想一想：这样的运算能像平方、立方那样简写吗？

三、有理数乘方的概念

一般地，n个相同的因数a相乘，记作a^n，读作“a的n次幂（或a的n次方）”，即

            a·a·a·a·a······a=a^n

n个

例如：2×2×2×2   记作2^4      读作2的4次方（幂）

2×2×2×2×2×2    记作2^6     读作2的6次方（幂）。

这种求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂。

一个数可以看作这个数本身的一次方，例如，8就是8^1，指数1通常省略不写。

因为a^n就是n个a相乘，所以可以利用有理数的乘法运算来进行有理数的乘方运算。

四、典例解析

有理数的乘方概念

例1：填一填：

（1）（−5）^2的底数是_______,指数是_______，（−5）^2表示2个_____相乘，读作______的2次方，也读作-5的________。

（2）（1/2）^6表示______个1/2相乘,读作1/2的______次方，也读作1/2的____次  幂。其中1/2叫做_________，6叫做________。

幂的底数是负数或分数时应添上括号！

例2：探究-8^3和（−8）^3一样吗？有什么区别？

解：（−8）^3是指3个-8相乘

     -8^3是先把3个8相乘，然后取结果的相反数

所以-8^3和（−8）^3不一样。

例3：探究（2/3）^2和2^2/3一样吗？有什么区别？

解：（2/3）^2是指2个2/3相乘

     2^2/3是先把2个2相乘，然后再除以3

所以（2/3）^2和2^2/3不一样。

例4：计算：

（1）（−4）^3（2）（−2）^4（3）（−2/3）^3

解：（1）（−4）^3=（-4）×（-4）×（-4）=-64；

（2）（−2）^4=（-2）×（-2）×（-2）×（-2）=16；

（3）（−2/3）^3=（-2/3）×（-2/3）×（−2/3）=-8/27

负数的奇次幂是负数，负数的偶次幂是正数；

正数的任何次幂都是正数；

0 的任何正整数次幂都是 0。

任何数的偶次幂都是非负数，即a^2≥0.

五、当堂小测

1.把下列各式写成幂的形式：

（1）（+2/5）×（+2/5）×（+2/5）×（+2/5）

（2）(-3.7)×(-3.7)×(-3.7)×(-3.7)×5×5

（3）xxxxxxyy

2.计算：

（1）（−4）^3     （2）-4^3    （3）（−3）^4     （4）-3^4    

（5）（3/5）^3    （6）3^3/5    （7）（2×3）^2    （8）2×3^2

3.比较（−4）^3和-4^3，下列说法正确的是（　　）

A．它们底数相同，指数也相同              

B．它们底数相同，但指数不相同

C．它们所表示的意义相同，但运算结果不相同 

D．虽然它们底数不同，但运算结果相同

4.计算：（−1）^2009的结果是(     )．

A．-1    B．1    C．-2009    D．2009

5.下列说法中，正确的是（  ）

A．一个数的平方一定大于这个数；  B．一个数的平方一定是正数；

C．一个数的平方一定小于这个数；   D．一个数的平方不可能是负数.

6. 下列各组数中，计算结果相等的是 (    )．

A．-2^3与（−2）^3      B．-2^2与（−2）^2  

C．（2/5）^2与2^2/5   D．-（-2）与-|-2|

7.不做运算，判断下列各运算结果的符号．

（−2）^7，（−3）^24，（−1.0009）^2009，-(−2)^2010

六、课堂小结

1.求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂。

读作“a的n次幂（或a的n次方）”。

2.负数的奇次幂是负数，负数的偶次幂是正数；

   正数的任何次幂都是正数；

   0 的任何正整数次幂都是 0。

   任何数的偶次幂都是非负数，即a^2≥0.

布置作业

1.计算：（1）3^4 ； −3^4 ；    (−3)^4；    -(−3)^4；

（2）2^3/3 ；   （2/3）^3；   （−2/3）^3 ；  -（−2）^3/3

2.下列说法正确的是（ ）

A．2^3 表示 2×3         B．﹣3^2 与（−3）^2互为相反数

C．（−4）^2 中﹣4 是底数，2 是幂 D．a^3=（−a）^3

3.已知(－ab)·(－ab)·(－ab)＞0，则（ ）

A．ab＜0 B．ab＞0 C．a＞0，b＜0 D．a＜0，b＜0

4.若 n 为正整数，（−1）^2n=（ ）

A．1    B． ﹣1 C．2n      D．不确定

5.若|x^3|=-x^3，则x是______；若|x^2| =-|x^2|，则 x^2是________；

6.1 米长的小棒，第 1 次截去一半，第 2 次截去剩下的一半，如此截下去， 第 7 次后剩下的小棒有多长？

板书设计

课程小结部分

教学反思

1.注意乘方计算与乘法法则的相似性。

2.强调计算时先定符号再定结果，易错点乘方的底数多举例子弄清实质。