人教版1.4.1 有理数的乘法备课课件ppt

这是一份人教版1.4.1 有理数的乘法备课课件ppt，共24页。

1.有理数乘法法则：
两数相乘，同号得正，异号得负，并把绝对值相乘． 任何数同0相乘，都得0.
2×(－3)＝______
(－6) ×(－4)＝______
24×(－5)＝______
想一想：2×(－3)×(－4)×(－5)该如何计算呢？
观察下面各式，它们的积是正的还是负的？
2×3×4×(－5)2×3×(－4)×(－5)2×(－3)×(－4)×(－5)(－2)×(－3)×(－4)×(－5)
几个不等于0的数相乘，积的符号与负因数的个数之间有什么关系？
几个不是0的数相乘， 负因数的个数是偶数时，积是正数； 负因数的个数是奇数时，积是负数.
多个不是0的数相乘,先做哪一步,再做哪一步？
再把各个乘数的绝对值相乘，作为积的绝对值.
1.若五个有理数的积为负数，那么这五个数中负因数的个数是( ) A.1 B.3 C.5 D.1或3或5
你能看出下式的结果吗？如果能，请说明理由．
几个数相乘，如果其中有因数为0，积等于0.
任何数与0相乘，都得0.
判断下列各式乘积的符号： ①(－3)×(－4)×(＋5.5)； ②4×(－2)×(－3.1)×(－7)； ③(－201)×0×7×(－2)； ④(－3.7)×(－6)×10×(－5.3)×(－1)， 其中积为正数的有________， 积为负数的有____________， 积为0的是_______________．(只填写序号)
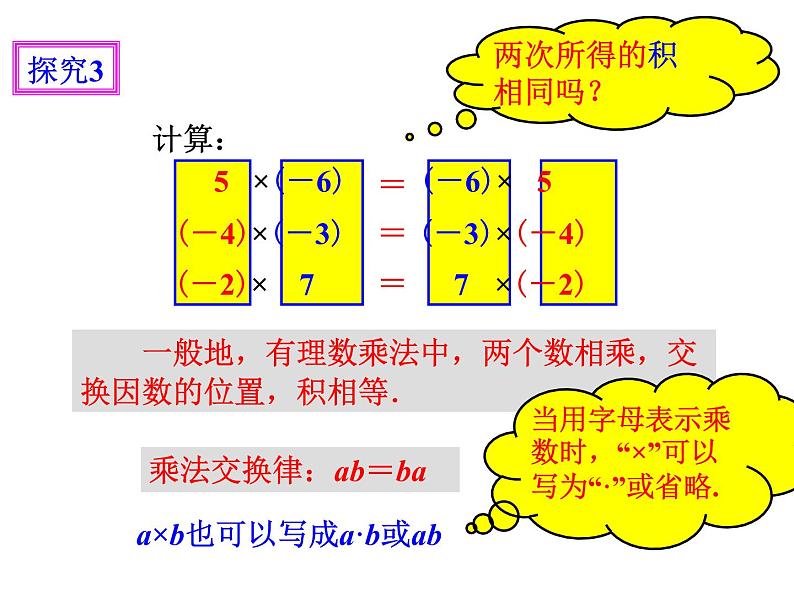
计算：　 5 ×(－6) (－6)× 5
(－4)×(－3) (－3)×(－4)
(－2)× 7 7 ×(－2)
一般地，有理数乘法中，两个数相乘，交换因数的位置，积相等．
乘法交换律：ab＝ba
a×b也可以写成a·b或ab
当用字母表示乘数时，“×”可以写为“·”或省略.
计算： [3×(－4)]×(－5) 3×[(－4)×(－5)]
你能得出什么结论呢？
一般地，有理数乘法中，三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等．
乘法结合律：(ab)c＝a(bc)
[3×(－4)]×(－5)＝(－12 )×(－5)＝60
3×[(－4)×(－5)]＝3×20＝60
计算： 5×[3＋(－7)] 5×3＋5×(－7)
一般地，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．
分配律：a(b＋c)＝ ab＋ac
5×[3＋(－7)]＝5×(－4)＝－20
5×3＋5×(－7) ＝15＋(－35)＝－20
今天我们学习了哪些知识？
1．我们学习了哪些乘法运算律？ 2．进行有理数的乘法运算时，哪些情况下考虑使用乘法运算律呢？
1.下列计算正确的是( )A.(－9)×5×(－4)×0＝9×5×4＝180B.－5×(－4)×(－2)×(－2)＝5×4×2×2＝80C.(－12)×( － －1)＝－8－3－1＝－12 D.－2×5－2×(－1)－(－2)×2＝－2×(5＋1－2)＝－8
2.用简便方法计算：(－23)×25－6×25＋18×25＋25，逆用分配律正确的是( ) A.25×(－23－6＋18)　 B.25×(－23－6＋18＋1) C.－25×(23＋6＋18) D.－25×(23＋6－18＋1)
4. 在等式4×□－2×□＝30的两个方格中分别填入一个数，使这两个数互为相反数，且等式成立，则第一个方格内的数是________．
教材38页习题1.4第7(1)(2)(3)题．