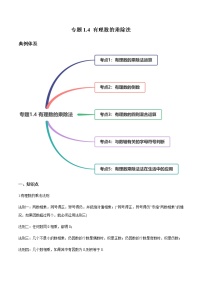
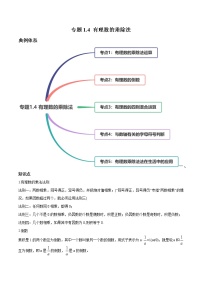
初中数学人教版七年级上册1.4.1 有理数的乘法精品练习
展开专题1.4 有理数的乘除法
典例体系
一、知识点
1.有理数的乘法法则
法则一:两数相乘,同号得正,异号得负,并把绝对值相乘;(“同号得正,异号得负”专指“两数相乘”的情况,如果因数超过两个,就必须运用法则三)
法则二:任何数同0相乘,都得0;
法则三:几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数;
法则四:几个数相乘,如果其中有因数为0,则积等于0.
2.倒数
乘积是1的两个数互为倒数,其中一个数叫做另一个数的倒数,用式子表示为a·=1(a≠0),就是说a和互为倒数,即a是的倒数,是a的倒数。
注意:①0没有倒数;
②求假分数或真分数的倒数,只要把这个分数的分子、分母点颠倒位置即可;求带分数的倒数时,先把带分数化为假分数,再把分子、分母颠倒位置;
③正数的倒数是正数,负数的倒数是负数。(求一个数的倒数,不改变这个数的性质);
④倒数等于它本身的数是1或-1,不包括0。
3.有理数的乘法运算律
⑴乘法交换律:一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等。即ab=ba
⑵乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。即(ab)c=a(bc).
⑶乘法分配律:一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,在把积相加。即a(b+c)=ab+ac
4.有理数的除法法则
(1)除以一个不等0的数,等于乘以这个数的倒数。
(2)两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0
5.有理数的乘除混合运算
(1)乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果。
(2)有理数的加减乘除混合运算,如无括号指出先做什么运算,则按照‘先乘除,后加减’的顺序进行。
二、考点点拨与训练
考点1:有理数的乘除法运算
典例:(2020·浙江省初三二模)计算:的结果是( )
A. B.12 C.1 D.
【答案】D
【解析】
解:
故选D.
方法或规律点拨
本题考查了有理数的乘法法则,注意符号,熟练掌握乘法法则是解题的关键.
巩固练习
1.(2020·天津初三二模)计算的结果等于( )
A. B.12 C. D.81
【答案】A
【解析】
.
故选:A.
2.(2020·广东省初三其他)计算的结果是( )
A. B.1 C. D.2
【答案】A
【解析】
根据两数相乘异号得负判断符号为负,则=-=-1.
故选A.
3.(2020·四川省初一期末)以下关于0的说法:①0的相反数与0的绝对值都是0;②0的倒数是0;③0减去一个数,等于这个数的相反数;④0除以任何有理数仍得0.其中说法正确的有( )个
A.1 B.2 C.3 D.4
【答案】B
【解析】
解:①0的相反数与0的绝对值都是0,正确;
②0没有倒数,故此项不正确;
③0减去一个数,等于这个数的相反数,正确;
④0除以任何非零有理数仍得0,故此项错误;
综上正确的有①③.
故选:B
4.(2020·天津初三学业考试)计算的值是( )
A.-12 B.-2 C.35 D.-35
【答案】C
【解析】原式
故选:C.
5.(2020·天津初三二模)计算:(﹣3)×5的结果是( )
A.﹣15 B.15 C.﹣2 D.2
【答案】A
【解析】
解:(﹣3)×5=-15,
故选:A.
6.(2020·长沙市一中湘一南湖学校初二月考)若a<c<0<b,则abc与0的大小关系是( )
A.abc<0 B.abc=0
C.abc>0 D.无法确定
【答案】C
【解析】
∵a<c<0<b,
∴abc>0.
故选C.
7.(2017·全国初一课时练习)计算时,应该运用( ).
A.加法交换律 B.乘法分配律
C.乘法交换律 D.乘法结合律
【答案】B
【解析】
∵原式=
=4+3-6
=1
∴应该运用乘法的分配律;
故选B.
8.(2017·全国初一课时练习)计算:(-4)×0.25=__________,(+4)×(-)=______,(-)×(-)=_______.
【答案】-1, -,
【解析】
∵(-4)×0.25=-1,
(+4)×(-)=-,
(-)×(-)=.
故答案为(1). -1, (2). -, (3).
考点2:有理数的倒数
典例:(2020·安徽省初三其他)-5的倒数是( )
A.-5 B.5 C. D.
【答案】D
【解析】
∵
∴-5的倒数是.
故选D.
方法或规律点拨
本题考查了倒数的性质,乘积为”1”的两个数互为倒数.
巩固练习
1.(2020·深圳市龙岗区南湾街道沙湾中学初三其他)-2的倒数是( )
A.-2 B. C. D.2
【答案】B
【解析】
-2的倒数是-
故选B
2.(2020·甘肃省武威市第十中学初三三模)的倒数是( )
A. B. C. D.
【答案】A
【解析】的倒数是,
故选A.
3.(2020·河北省初三学业考试)-2020的倒数是( )
A. B. C.2020 D.
【答案】B
【解析】∵-2020×()=1,
∴-2020的倒数是.
故选:B.
4.(2020·广东省初三其他)6的倒数是( )
A.﹣6 B.6 C. D.﹣
【答案】C
【解析】
6的倒数是,
故选C.
5.(2020·四川省初三)下列选项中,两数互为倒数的是( )
A.5与 B.与 C.2020与 D.2020与
【答案】D
【解析】解:A. 5与互为相反数,而非互为倒数,故该选项与题意不符;
B. 的到数是 ,而的到数是2020,故本选项错误;
C. 2020与互为相反数,而非互为倒数,故该选项与题意不符;
D. 2020与互为倒数,故本选项与题意相符.
故选D.
6.(2020·云南省初三三模)的倒数的绝对值是___________.
【答案】
【解析】的倒数为,的绝对值为
7.(2019·北京市顺义区杨镇第二中学初一期中)﹣1的倒数是__,相反数是__绝对值是__.
【答案】, ,
【解析】
解:∵,
∴﹣1的倒数是,相反数是,绝对值是,
故答案为:,,.
8.(2018·云南省初一期末)已知互为相反数,互为倒数,m的绝对值为3,那么的值是________ .
【答案】2016或1986
【解析】
解:根据题意得:a+b=0,cd=1,m=3或﹣3,
当m=3时,原式=,
当m=﹣3时,原式=,
∴的值为:2016或1986.
故答案为:2016或1986
9.(2019·重庆实验外国语学校初一期中)如果a,b互为相反数,c,d互为倒数,m的绝对值是3,则m2﹣2019a+5cd﹣2019b的值是____.
【答案】14.
【解析】∵a,b互为相反数,c,d互为倒数,m的绝对值是3,
∴a+b=0,cd=1,m=±3,
则m2﹣2019a+5cd﹣2019b
=9﹣2019(a+b)+5cd
=9﹣0+5
=14.
故答案为:14.
考点3:有理数的四则混合运算
典例:(2019·山东省初一期中)学习有理数的乘法后,老师给同学们这样一道题目:计算:49×(-5),看谁算的又快又对,有两位同学的解法如下:
聪聪;原式=-×5=--249;
明明:原式=(49+)×(-5)=49×(-5)+×(-5)=-249,
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:39×(-8).
【答案】(1)明明解法较好;(2)还有更好的解法,解法见解析;(3)﹣319.
【解析】
解:(1)明明解法较好;
(2)还有更好的解法,如下:
原式=(50﹣)×(﹣5)
=﹣250+
=﹣249;
(3)原式=(40﹣)×(﹣8)
=﹣320+
=﹣319.
方法或规律点拨
本题考查了有理数的乘法,主要是对乘法分配律的应用,把带分数进行适当的转化是解题的关键.
巩固练习
1.(2019·北京市顺义区杨镇第二中学初一期中)如图是一个简单的数值运算程序,当输入的x的值为—2时,输出的数值为_________.
【答案】-1
【解析】
当输入-2时,带入程序列式为:(-2)×(-1)-3=2-3=-1.
故答案为:-1.
2.(2020·北京初三月考)对于两个非零整数x,y,如果满足这两个数的积等于它们的和的6倍,称这样的x,y为友好整数组,记作
【答案】见解析 9
【解析】
由已知可得若为友好整数组,则xy≠0,且xy=6(x+y)
∴(x-6)y=6x,显然当x=6时该等式不成立,
∴x≠6
∴
∵y是整数
∴是整数
∴当x-6=1,即x=7时,y=42,故<7,42>是一个友好整数组.
∵x,y是整数
∴是整数,且x-6是整数
∵xy≠0,且<x,y>与<y,x>视为相同的友好整数组.
∴x-6=±1或±2或±3或±4或-6,
∴这样的友好整数组一共有2+2+2+2+1=9(组).
故答案为:<7,42>;9.
3.利用运算律有时能进行简便计算.
例1
例2
计算:(1);
(2)
【答案】(1);(2)23
【解析】
(1)
;
(2)
.
4.(2019·北京市顺义区杨镇第二中学初一期中)
【答案】-17
【解析】解:原式=
=
=-24+12+9-14
=-17.
5.(2020·成都市金花中学初一期中)用简便方法计算下列各式的值:
(1)
(2)
【答案】(1)-15;(2)0.
【解析】解:
=
=
=
=-15;
(2)
=
=
=0.
6.(2017·全国初一课时练习)学习了有理数的运算后,老师给同学们布置了下面一道题:
计算:,看谁算得又对又快.
下面是甲、乙两名同学给出的解法:
甲:原式= ,
乙:原式=
你认为谁的解法好?你还能想出别的简便方法吗?试一下!
【答案】-
【解析】
乙的解法好,还有方法如下:
原式.
7.(2020·河北省初三一模)计算下列各式的值.
(1)(﹣53)+(+21)﹣(﹣69)﹣(+37)
(2)﹣3.61×0.75+0.61×+(﹣0.2)×75%.
【答案】(1)0;(2)-2.4
【解析】
解:(1)(﹣53)+(+21)﹣(﹣69)﹣(+37)
=﹣53+21+69﹣37
=﹣90+90
=0;
(2)
=﹣3.61×0.75+0.61×0.75+(﹣0.2)×0.75
=0.75×(﹣3.61+0.61﹣0.2)
=0.75×(﹣3.2)
=﹣2.4.
8.(2019·吉林省东北师大附中初一月考)已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
【答案】(1)-6;(2);(3)不满足,举例见解析
【解析】
解:(1)(-2)×4-(-2)=-8+2=-6
(2)
(3)∵新运算
∴运用加法加法交换律可得:
假设,
则=3×4-3=9
=4×3-4=8
∴不能用交换律.
考点4:与数轴有关的字母符号判断
典例:(2020·北京初三二模)实数a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( )
A.|a|<|b| B.ad>0 C.a+c>0 D.d-a>0
【答案】D
【解析】
由实数a,b,c,d在数轴上对应的点的位置可知,a<b<0<c<d,
∴|a|>|b|,ad<0,a+c<0,d-a>0,
因此选项D正确,
故选:D.
方法或规律点拨
本题考查数轴表示数,有理数的四则运算法则,理解符号、绝对值是确定有理数的必要条件.
巩固练习
1.(2020·山西省初一期末)如图所示,A.B两点在数轴上表示的数分别为、,下列式子成立的是( )
A. B. C. D.
【答案】C
【解析】∵a<0,b>0,
∴,故A选项错误;
∵a<b,
∴,故B选项错误;
∵-a>0,b>0,,
∴ ,故C选项正确;
∵a<0,b>0,,
∴,故D选项错误.
故选C.
2.(2020·全国初一)如图,在数轴上,实数的对应点分别为点,则( )
A.1.5 B.1 C. D.
【答案】C
【解析】解:由数轴得a=-0.5,b=2,
∴ab=(-0.5)×2=-1.
故选:C
3.(2020·河北省初三学业考试)如图,在数轴上表示点的倒数的点可能是( )
A.点 B.点 C.点 D.点
【答案】A
【解析】
由图可得,点P在0到1之间且靠近1,则表示点的倒数的点可能在1到2之间,即点A.
故选:A.
4.(2020·山东省济宁学院附属中学初三二模)实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
A.a<﹣1 B.ab>0 C.a﹣b<0 D.a+b<0
【答案】C
【解析】选项A,从数轴上看出,a在﹣1与0之间,
∴﹣1<a<0,
故选项A不合题意;
选项B,从数轴上看出,a在原点左侧,b在原点右侧,
∴a<0,b>0,
∴ab<0,
故选项B不合题意;
选项C,从数轴上看出,a在b的左侧,
∴a<b,
即a﹣b<0,
故选项C符合题意;
选项D,从数轴上看出,a在﹣1与0之间,
∴1<b<2,
∴|a|<|b|,
∵a<0,b>0,
所以a+b=|b|﹣|a|>0,
故选项D不合题意.
故选:C.
5.(2020·北京初三二模)实数,,在数轴上的对应点的位置如图所示,则下列结论正确的是( )
A. B. C. D.
【答案】D
【解析】解:由题意得:
A错误,B错误,C错误,D正确.
故选D.
6.(2020·江西省初一期末)有理数a,b在数轴上的表示如图所示,则下列结论中:①ab<0;②ab>0;③a+b<0;④a﹣b<0;⑤a<|b|;⑥﹣a>﹣b,正确的有( )
A.3个 B.4个 C.5个 D.6个
【答案】A
【解析】
由数轴得b<0
∴①、③、⑤正确,②、④、⑥错误,
故选:A
7.(2020·北京四中初三月考)如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是( )
A.一定在点A的左侧 B.一定与线段AB的中点重合
C.可能在点B的右侧 D.一定与点A或点B重合
【答案】C
【解析】∵数轴上A,B两点所表示的数互为倒数,∴A,B两点所表示的数符号相同,如果A,B两点所表示的数都是正数,那么原点在点A的左侧;
如果A,B两点所表示的数都是负数,那么原点在点B的右侧,∴原点可能在点A的左侧或点B的右侧.
故选C.
8.(2019·浙江省初三二模)有理数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
A.a>﹣4 B.bd>0 C.|a|>|b| D.b+c>0
【答案】C
【解析】解:由数轴上点的位置,得
a<﹣4<b<0<c<1<d.
A、a<﹣4,故A不符合题意;
B、bd<0,故B不符合题意;
C、∵|a|>4,|b|<2,∴|a|>|b|,故C符合题意;
D、b+c<0,故D不符合题意;
故选:C.
9.(2019·浙江省初三期中)若实数在数轴上的位置如图所示,则下列判断不正确的是( )
A. B. C. D.的绝对值相等
【答案】D
【解析】解:由数轴上x、y两点的位置可知,y<0<x,且|x|>|y|,
A、x>0,故本选项正确;
B、∵y<0,x>0,∴xy<0,故本选项正确;
C、x>y,故本选项正确;
D、|x|>|y|,故本选项错误.
故选:D.
考点5:有理数乘除法法在生活中的应用
典例:(2018·湖南广益实验中学初一月考)一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
【答案】(1)见解析;(2)5千米;(3)9升.
【解析】解:(1)如图所示:
(2)由小明与小刚在数轴上的位置可得:千米
(3)这辆货车此次送货共耗油:升
方法或规律点拨
本题是一道典型的有理数混合运算的应用题,解题的关键是要掌握能够将应用问题转化为有理数的混合运算的能力,数轴正是表示这一问题的最好工具.
巩固练习
1.(2020·广东省初一期末)检修工乘汽车沿东西方向检修电路,规定向东为正,向西为负,某天检修工从A地出发,到收工时行程记录为(单位:千米)
+8,﹣9,+4,﹣7,﹣2,﹣10,+11,﹣3,+7,﹣5;
(1)收工时,检修工在A地的哪边?距A地多远?
(2)若每千米耗油0.3升,从A地出发到收工时,共耗油多少升?
【答案】(1)A地的西边;距A地6千米
(2)19.8升
【解析】
解:(1)(+8)+(﹣9)+(+4)+(﹣7)+(﹣2)+(﹣10)+(+11)+(﹣3)+(+7)+(﹣5)
=8﹣9+4﹣7﹣2﹣10+11﹣3+7﹣5=8+4+11+7﹣9﹣7﹣2﹣10﹣3﹣5=30﹣36=﹣6(千米),
答:收工时,检修工在A地的西边,距A地6千米;
(2)|+8|+|﹣9|+|+4|+|﹣7|+|﹣2|+|﹣10|+|+11|+|﹣3|+|+7|+|﹣5|
=8+9+4+7+2+10+11+3+7+5=66(千米)
66×0.3=19.8(升)
答:从A地出发到收工时,共耗油19.8升.
2.(2020·山东省初一期末)一辆出租车从超市(点)出发,向东走到达小李家(点),继续向东走到达小张家(点),然后又回头向西走到达小陈家(点),最后回到超市.
(1)以超市为原点,向东方向为正方向,用表示,画出数轴,并在该数轴上表示、、、的位置;
(2)小陈家(点)距小李家(点)有多远?
(3)若出租车收费标准如下,以内包括收费元,超过部分按每千米元收费,则从超市出发到回到超市一共花费多少元?
【答案】(1)见解析;(2)6千米;(3)61元.
【解析】
(1)根据数轴与点的对应关系,可知超市(O点)在原点,小李家(点)所在位置表示的数是+2,小张家(点)所在位置表示的数是+6,小陈家(点)所在位置表示的数是-4,画出数轴如图所示:
(2)从数轴上值,小陈家(点)和小李家(点)距离为:2-(-4)=6(千米);
(3)一共行驶了:2+4+10+4=20(千米),
则一共花费了:10+(20-3)×3=61(元),
则从超市出发到回到超市一共花费61元.
3.(2019·全国初一课时练习)一只小虫沿一根东西方向放着的木杆爬行,先以每分钟m的速度向西爬行,后来又以同样的速度向东爬行,试求它向西爬行4分钟,又向东爬行6分钟后距出发点的距离.
【答案】5.5m
【解析】规定向东为正,向西为负,则有m,即最终离出发点的距离是m.
4.(2019·内蒙古自治区初一期末)某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km),依先后次序记录如下:+10,﹣3、﹣4、+4、﹣9、+6、﹣4、﹣6、﹣4、+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若平均每千米的价格为2.4元,司机一个下午的营业额是多少?
【答案】(1)将最后一名乘客送到目的地,出租车回到鼓楼出发点;(2)144元
【解析】
(1)
故将最后一名乘客送到目的地,出租车回到鼓楼出发点;
(2)
因为平均每千米的价格为元
所以司机一个下午的营业额是(元)
答:司机一个下午的营业额是144元.
5.(2020·广东省东莞市中堂星晨学校初一月考)邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
【答案】(1)见解析;(2)点与点的距离为;共耗油量为升.
【解析】依题意得,数轴为:
;
依题意得:点与点的距离为:;
依题意得邮递员骑了:,
∴共耗油量为:升.
6.(2019·江苏省苏州工业园区金鸡湖学校初一一模)在某地区,高度每升高100米,气温下降0.8 ℃.若在该地区的山脚测得气温为15 ℃,在山顶测得气温为-5 ℃,你能求出从山顶到山脚的高度吗?
【答案】山顶到山脚的高度为2500米.
【解析】
因为山顶和山脚的温度差为15+5=20℃,所以山顶到山脚的高度为:20÷0.8×100=2500(米).
答:山顶到山脚的高度为2500米.
7.(2019·江苏省初一一模)为了有效控制酒后驾车,某市城管的汽车在一条东西方向的公路上巡逻,若规定向东为正,向西为负,从出发点开始所走的路程为(单位:千米):
此时,这辆城管的汽车司机如何向队长描述他所处的位置?
如果队长命令他马上返回出发点,这次巡逻(含返回)共耗油多少升?(已知每千米耗油升)
【答案】(1)这辆城管的汽车司机在出发点以东3千米处;(2)这次巡逻(含返回)共耗油3升.
【解析】
(1)(千米),
答:这辆城管的汽车司机在出发点以东3千米处;
(2)(千米),
∴(升),
答:这次巡逻(含返回)共耗油3升.
8.(2019·河南省初一期中)某自行车厂一周内计划平均每天生产200辆自行车,由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正,减产记为负):
星期
一
二
三
四
五
六
日
增减产量/辆
(1)根据记录的数据可知,该厂星期五生产自行车 辆.
(2)根据上表记录的数据可知,该厂本周实际生产自行车 辆.
(3)该厂实行每日计件工资制,每生产一辆自行车可得60元,若超额完成任务,则超过部分每辆另外奖励15元,若完不成每天的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
(4)若该厂实行每周计件工资制,每生产一辆自行车可得60元,若超额完成周计划工作量,则超过部分每辆另外奖励15元,若完不成每周的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
【答案】(1) 190;(2) 1409;(3) 84550 元;(4) 84675元.
【解析】解:(1)∵超产记为正、减产记为负,
∴星期五生产自行车(辆),
故答案为:190;
(2)该厂本周实际生产自行车:
(辆),
故答案为:1409;
(3)(辆),
(元),
答:该厂工人这一周的工资总额是84550 元;
(4)实行每周计件工资制的工资为(元),
答:该厂工人这一周的工资总额是84675元.
人教版七年级上册第四章 几何图形初步4.3 角4.3.1 角精品习题: 这是一份人教版七年级上册第四章 几何图形初步4.3 角4.3.1 角精品习题,文件包含专题43角讲练-2022-2023学年七年级上册同步讲练解析版人教版docx、专题43角讲练-2022-2023学年七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
人教版七年级上册2.2 整式的加减精品随堂练习题: 这是一份人教版七年级上册2.2 整式的加减精品随堂练习题,文件包含专题22整式的加减讲练-2022-2023七年级上册同步讲练解析版人教版docx、专题22整式的加减讲练-2022-2023七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
初中数学2.1 整式优秀练习题: 这是一份初中数学2.1 整式优秀练习题,文件包含专题21整式讲练-2022-2023七年级上册同步讲练解析版人教版docx、专题21整式讲练-2022-2023七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。