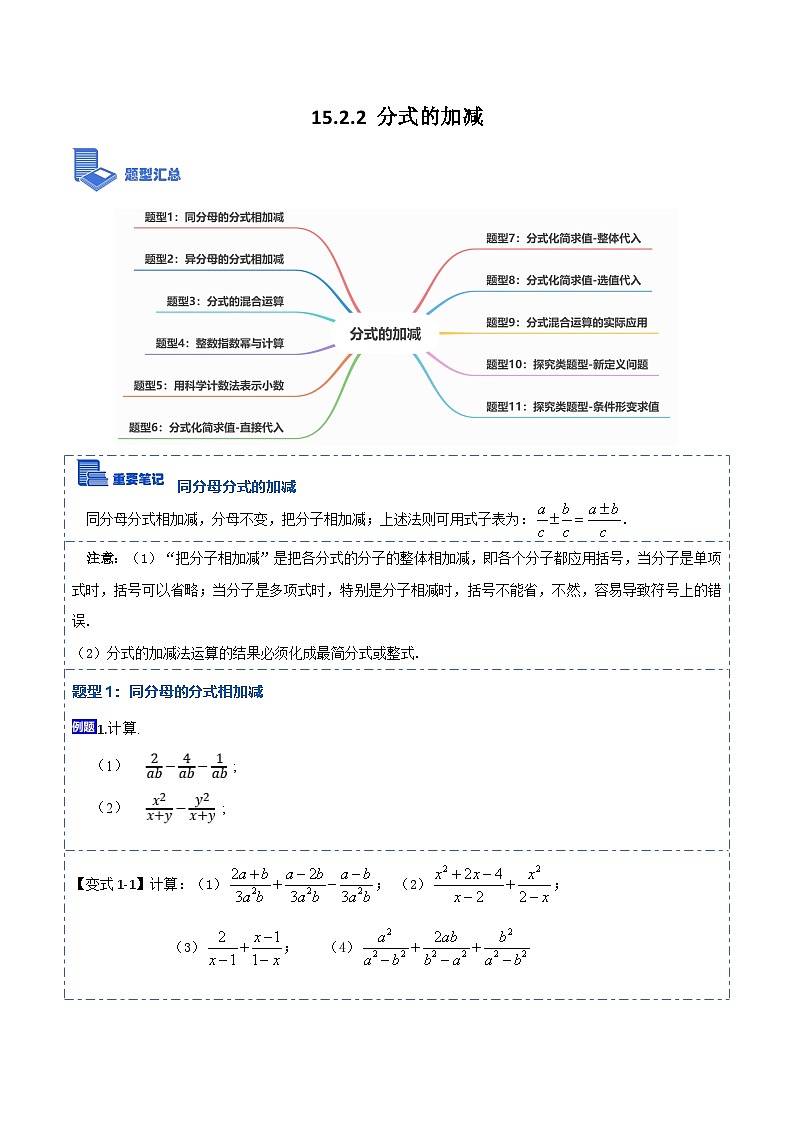
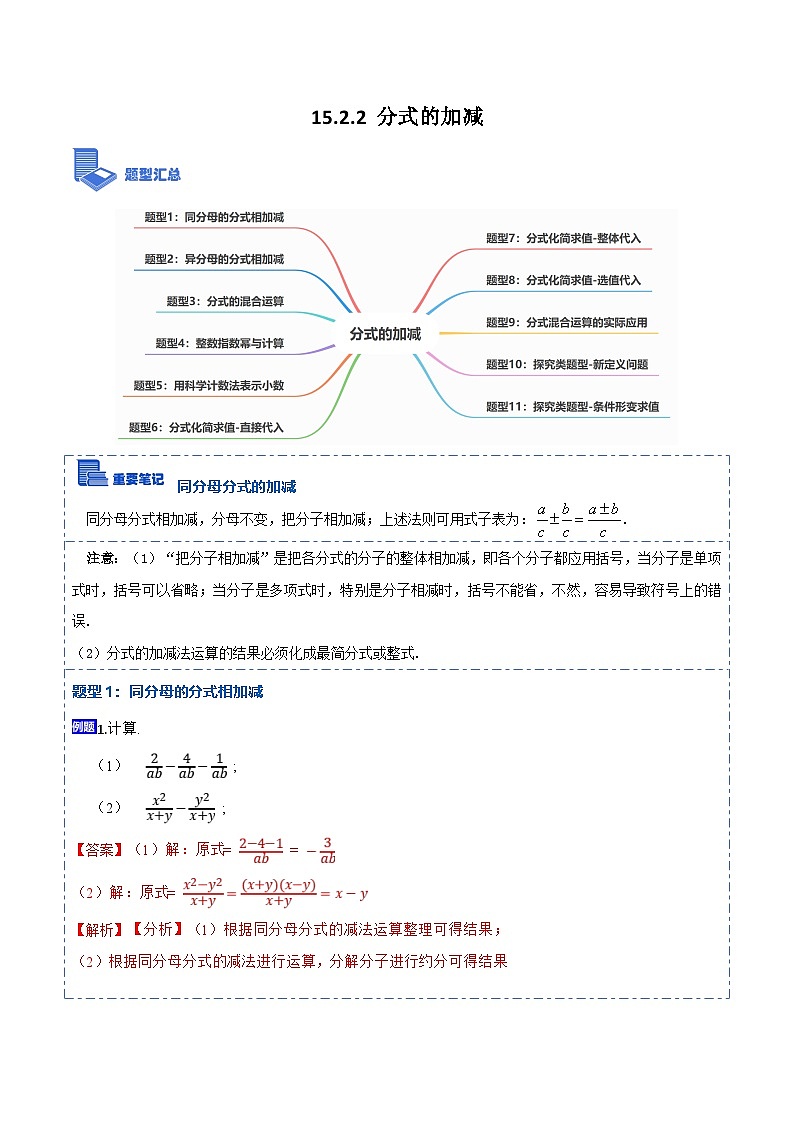
人教版（2024）八年级上册15.2.2 分式的加减同步测试题

这是一份人教版（2024）八年级上册15.2.2 分式的加减同步测试题，文件包含人教版数学八上考点精讲精练1522分式的加减11大题型原卷版doc、人教版数学八上考点精讲精练1522分式的加减11大题型解析版doc等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

一、单选题
1．化简 的结果是（ ）
A．x+1B．x﹣1C．xD．﹣x
2．若a+2b＝0，则分式（ + ）÷ 的值为（ ）
A．B．C．﹣ D．﹣3b
3．化简 + 的结果是（ ）
A．x﹣2B．C．D．
4．已知 ，则A的取值是（ ）
A．-3B．3C．-6D．6
5．化简﹣的结果是（ ）
A．B．C．D．
二、填空题
6． 计算的结果是 .
7．计算÷（1﹣）的结果是 ．
8．如果 ，那么代数式 的值是 ．
9．若 ， ，则 的值是 ．
三、解答题
10．先化简，再求值：（1﹣ ）÷ ，从﹣1，2，3中选择一个适当的数作为x值代入．
11．先化简，再求值： ，其中 ．
12．先化简，再求值：．其中x为不等式组的整数解．
13．先化简，再求值： ，其中 ．
14．已知
（1）化简A；
（2）若 ，求A的值．
同分母分式的加减
同分母分式相加减，分母不变，把分子相加减；上述法则可用式子表为：.
注意：（1）“把分子相加减”是把各分式的分子的整体相加减，即各个分子都应用括号，当分子是单项式时，括号可以省略；当分子是多项式时，特别是分子相减时，括号不能省，不然，容易导致符号上的错误.
（2）分式的加减法运算的结果必须化成最简分式或整式.
题型1：同分母的分式相加减
1.计算.
（1） ;
（2） ;
【变式1-1】计算：（1）； （2）；
（3）； （4）
异分母分式的加减
异分母分式相加减，先通分，变为同分母的分式，再加减.上述法则可用式子表为：.
注意：（1）异分母的分式相加减，先通分是关键.通分后，异分母的分式加减法变成同分母分式的加减法.
（2）异分母分式加减法的一般步骤：①通分，②进行同分母分式的加减运算，③把结果化成最简分式.
题型2：异分母的分式相加减
2.计算：（1）．
（2）化简：．
（3） .
【变式2-1】（1）；（2）；（3）．
【变式2-2】计算：（1）；（2）.
分式的混合运算
与分数的加、减、乘、除混合运算一样，分式的加、减、乘、除混合运算，也是先算乘、除，后算加、减；遇到括号，先算括号内的，按先小括号，再中括号，最后大括号的顺序计算. 分式运算结果必须达到最简，能约分的要约分，保证结果是最简分式或整式.
注意：（1）正确运用运算法则：分式的乘除（包括乘方）、加减、符号变化法则是正确进行分式运算的基础，要牢牢掌握.
（2）运算顺序：先算乘方，再算乘、除，最后算加、减，遇有括号，先算括号内的.
（3）运算律：运算律包括加法和乘法的交换律、结合律，乘法对加法的分配律.能灵活运用运算律，将大大提高运算速度.
题型3：分式的混合运算
3.计算（1）
（a ）.
【变式3-1】计算：（1）；（2）．
【变式3-2】 （1）；
（2）．
零指数幂
任何不等于零的数的零次幂都等于1，即.
注意：同底数幂的除法法则可以推广到整数指数幂.即（，、为整数）当时，得到.
负整数指数幂
任何不等于零的数的（为正整数）次幂，等于这个数的次幂的倒数，即（≠0，是正整数）.
引进了零指数幂和负整数指数幂后，指数的范围已经扩大到了全体整数，以前所学的幂的运算性质仍然成立.
注意：是的倒数，可以是不等于0的数，也可以是不等于0的代数式.例如（），（）.
题型4：整数指数幂与计算
4.计算：（1）20210+（）﹣1．
（2）．
【变式4-1】计算：
【变式4-2】计算：
（1）
（2）-12020+（3.14-π）0-（- ）-2
科学记数法的一般形式
（1）把一个绝对值大于10的数表示成的形式，其中是正整数，
（2）利用10的负整数次幂表示一些绝对值较小的数，即的形式，其中是正整数，.
用以上两种形式表示数的方法，叫做科学记数法.
题型5：用科学计数法表示小数
5.新型冠状病毒的直径约为0.000000907米，0.000000907用科学记数法表示为（ ）
A．9.07×10-10 B．9.07×10-11 C．9.07×10-8 D．9.07×10-7
【变式5-1】用科学记数法表示：-3105000= ，；0.000305= 。
【变式5-2】人体红细胞与我们的生命活动息息相关，是通过血液运送氧气的最主要的媒介．红细胞的直径约为0.00000767米，请把数0.00000767用科学记数法表示为
题型6：分式化简求值-直接代入
6.已知x＝，对代数式先化简，再求值.
【变式6-1】先化简，再求值：，其中
【变式6-2】先化简，再求值：，其中．
题型7：分式化简求值-整体代入
7.已知，求代数式的值．
【变式7-1】已知，求代数式的值.
【变式7-2】已知 ，求 的值．
题型8：分式化简求值-选值代入
8.先化简分式，再从－2，－1，1，这4个数中选择一个合适的数作为a的值代入求值．
【变式8-1】先化简 ，再从 的范围内选取一个合适的整数代入求值.
【变式8-2】化简：，并从不等式组的解集中选择一个合适的整数解代入求值．
题型9：分式混合运算的实际应用
9.如图，A种小麦试验田是边长为a的正方形中减去一个边长为b的正方形蓄水池后余下的部分；B种小麦试验田是边长为（a+b）的正方形．
（1）设两块试验田都收获了m（kg）小麦，求A，B两种小麦单位面积产量的比．
（2）当a=2b时，A，B两种小麦单位面积产量哪个较大？
（3）若A，B两种小麦单位面积产量相同，求a,b满足的关系式．
【变式9-1】“杂交水稻之父”袁隆平团队示范基地的“水稻1号”的试验田是边长为a米（a＞1）的正方形去掉一个边长为1米的正方形蓄水池后余下的部分，“水稻2号”的试验田是边长为（a-1）米的正方形，两块试验田的水稻都收获了1000千克．
（1）试说明哪种水稻的单位面积产量高？
（2）高的单位面积产量是低的单位面积产量的多少倍？
题型10：探究类题型-新定义问题
10.定义新运算：a+b=，若a⊕（-b）=4，则的值是 。
【变式10-1】定义运算：a⊗b＝，比如2⊗3＝．下面给出了关于这种运算的几个结论：
①2⊗(−3)＝；
②此运算中的字母a,b均不能取零；
③a⊗b=b⊗a；
④a⊗（b+c）=a⊗b+a⊗c.
其中正确的是 ．（把所有正确结论都写在横线上）
【变式10-2】对于任意非零实数a,b,定义运算“☆”如下：a☆b=，则2☆1+3☆2+4☆3+…+2010☆2009+2011☆2010=
根据题中的新定义将所求式子变形，拆项抵消后即可得到结果．
题型11：探究类题型-条件形变求值
11.已知实数a、b、c满足 ；
计算： .
【变式11-1】比较大小有求差、求比等方法，但灵活应用已知巧妙变形也会起到简化计算的效果．已知a、b为实数，且ab=1，设P=+，Q=+，比较P、Q的大小．
【变式11-2】已知a、b、c均为非零的实数，且满足 = = ，求 的值．