(寒假)浙教版数学七年级寒假讲练测第07讲 平行线 单元综合检测（难点）（2份，原卷版+解析版）

这是一份(寒假)浙教版数学七年级寒假讲练测第07讲 平行线 单元综合检测（难点）（2份，原卷版+解析版），文件包含寒假浙教版数学七年级寒假讲练测第07讲平行线单元综合检测难点原卷版doc、寒假浙教版数学七年级寒假讲练测第07讲平行线单元综合检测难点解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
一、单选题
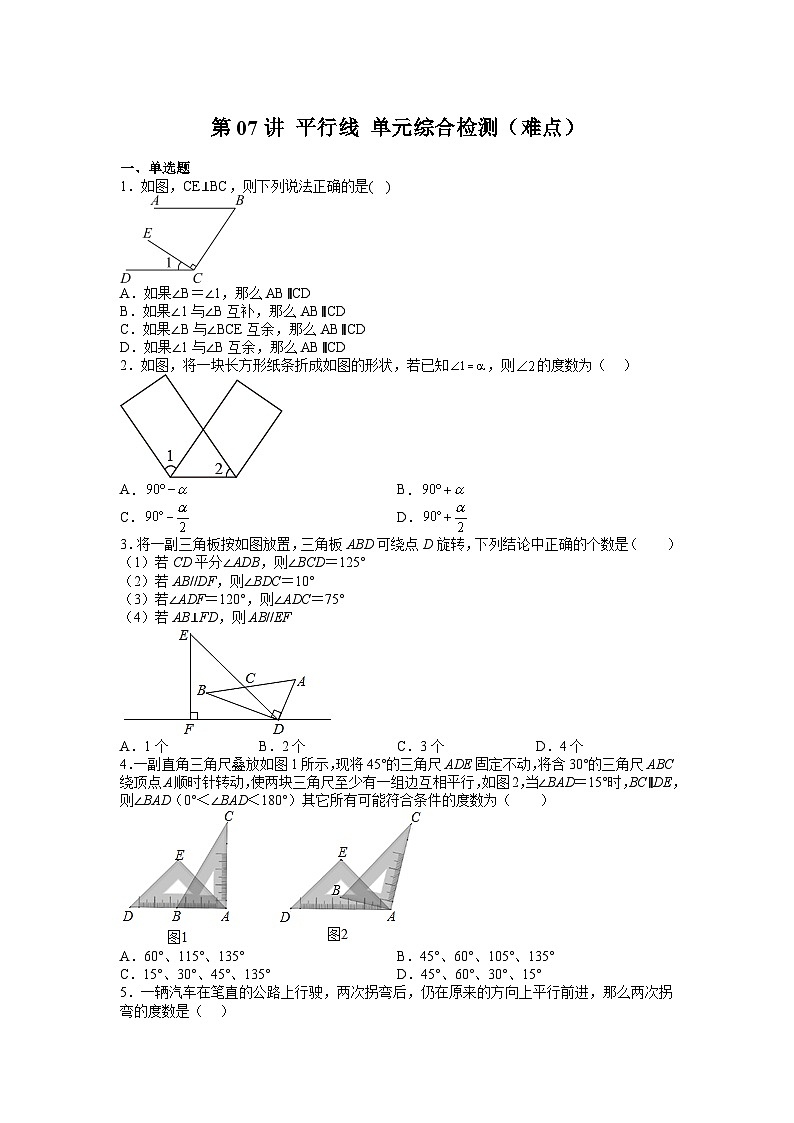
1．如图，CE⊥BC，则下列说法正确的是( )
A．如果∠B＝∠1，那么AB∥CD
B．如果∠1与∠B互补，那么AB∥CD
C．如果∠B与∠BCE互余，那么AB∥CD
D．如果∠1与∠B互余，那么AB∥CD
【答案】D
【分析】根据平行线的判定定理即可求解．
【解析】A、由于∠B和∠1不是同位角也不是内错角，故由∠B＝∠1不能判断AB∥CD，不符合题意；
B、由∠1与∠B不是同旁内角，故由∠1与∠B互补，不能判断AB∥CD，不符合题意；
C、由∠B与∠BCE互余，不能判断AB∥CD，不符合题意；
D、由同旁内角互补，两直线平行可知，如果∠1与∠B互余，则∠1+∠B+∠ECB=180°，故AD∥CD是正确的，符合题意．
故选D．
【点睛】此题考查了平行线的判定，关键是熟练掌握（1）定理1：两条直线被第三条所截，如果同位角相等，那么这两条直线平行． 简单说成：同位角相等，两直线平行．（2）定理2：两条直线被第三条所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行．（3）定理3：两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行．简单说成：同旁内角互补，两直线平行．（4）定理4：两条直线都和第三条直线平行，那么这两条直线平行．（5）定理5：在同一平面内，如果两条直线同时垂直于同一条直线，那么这两条直线平行．
2．如图，将一块长方形纸条折成如图的形状，若已知，则的度数为（ ）
A．B．
C．D．
【答案】C
【分析】由折叠性质可得∠3=（180°-∠1）÷2，再根据平行线性质可得．
【解析】由折叠性质可得∠3=（180°-∠1）÷2=（180°-α）÷2
由长方形对边平行可得∠1+∠2+∠3=180°
所以∠2=180°-∠1-∠3=180°-α-（180°-α）÷2=
故选：C
【点睛】考核知识点：平行线性质．理解折叠性质和平行线性质是关键．
3．将一副三角板按如图放置，三角板ABD可绕点D旋转，下列结论中正确的个数是（ ）
（1）若CD平分∠ADB，则∠BCD＝125°
（2）若AB//DF，则∠BDC＝10°
（3）若∠ADF＝120°，则∠ADC＝75°
（4）若AB⊥FD，则AB//EF
A．1个B．2个C．3个D．4个
【答案】A
【分析】由旋转的性质和平行线的性质与判定依次判断可求解．
【解析】解：（1）当CD平分∠ADB，则∠ADC＝45°，
∴∠BCD＝∠A＋∠ADC＝105°，故（1）错误；
（2）若AB∥DF，且AB在DF的上方，则∠ABD＝∠BDF＝30°，
∴∠BDC＝∠EDF−∠BDF＝15°，故（2）错误；
（3）若∠ADF＝120°时，且AD在DF的下方时，则∠ADC＝180°，故（3）错误；
（4）若AB⊥FD，且EF⊥DF，则EF∥AB，故（4）正确，
故选：A．
【点睛】本题考查了旋转的性质，平行线的判定和性质，掌握旋转的性质是解题的关键．
4．一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行，如图2，当∠BAD＝15°时，BC∥DE，则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为（ ）
A．60°、115°、135°B．45°、60°、105°、135°
C．15°、30°、45°、135°D．45°、60°、30°、15°
【答案】B
【分析】根据题意画出图形，再由平行线的性质定理即可得出结论．
【解析】解：如图
当∥时，；
当∥时，；
当∥ 时，∵，
∴；
当∥时，∵ ，
∴．
故选B
【点睛】本题考查的是平行线的判定与性质，根据题意画出图形，利用平行线的性质及直角三角板的性质求解是解答此题的关键．
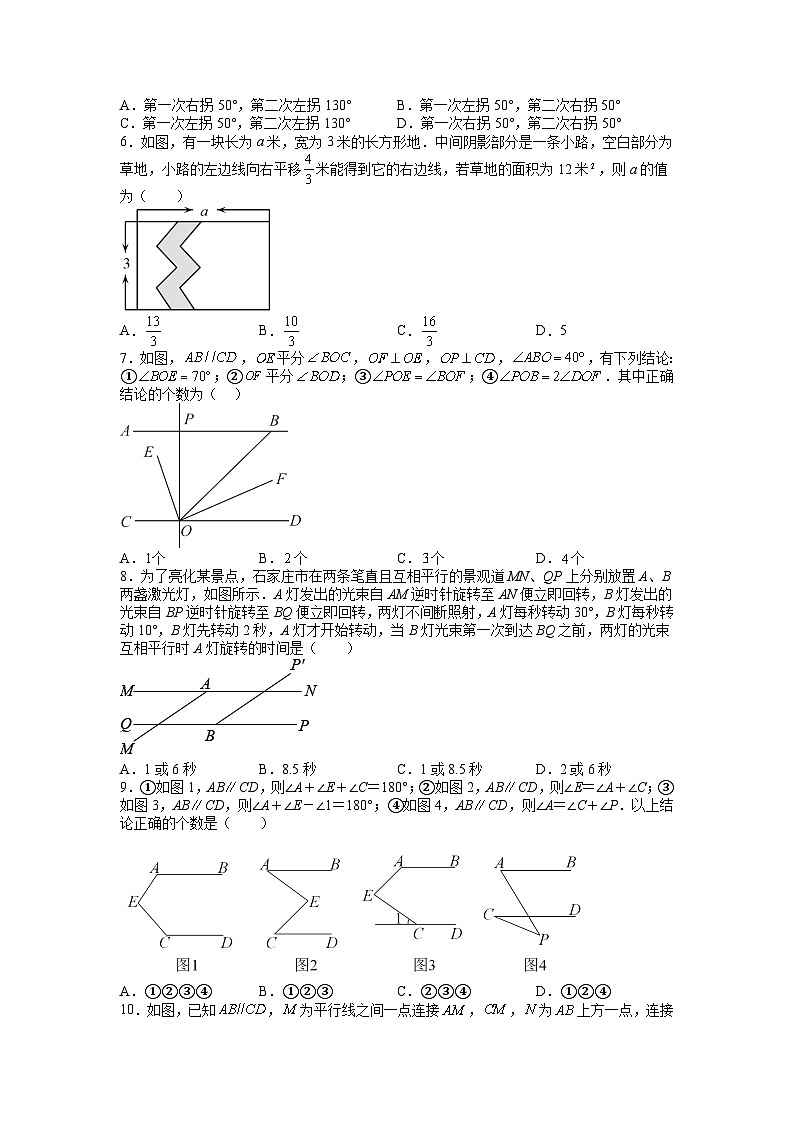
5．一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的度数是（ ）
A．第一次右拐50°，第二次左拐130°B．第一次左拐50°，第二次右拐50°
C．第一次左拐50°，第二次左拐130°D．第一次右拐50°，第二次右拐50°
【答案】B
【分析】根据两条直线平行的性质：两条直线平行，同位角相等．再根据题意得：两次拐的方向不相同，但角度相等．
【解析】解：如图，第一次拐的角是∠1，第二次拐的角是∠2，由于平行前进，可以得到∠1=∠2．
因此，第一次与第二次拐的方向不相同，角度要相同，
故只有B选项符合，
故选B．
【点睛】此题主要考查了平行线的性质，注意要想两次拐弯后，仍在原来的方向上平行前进，则拐的方向应相反，角度应相等．
6．如图，有一块长为a米，宽为3米的长方形地．中间阴影部分是一条小路，空白部分为草地，小路的左边线向右平移米能得到它的右边线，若草地的面积为12米，则a的值为（ ）
A．B．C．D．5
【答案】C
【分析】根据小路的左边线向右平移米能得到它的右边线，可得路的宽度是米，根据平移，可把路移到左边，再根据面积公式，可得答案．
【解析】解：依题意有，
解得．
故答案为：C
【点睛】本题考查了生活中的平移现象，难度不大，属于常考题型．
7．如图，，平分，，，，有下列结论：①；②平分；③；④．其中正确结论的个数为（ ）
A．个B．个C．个D．个
【答案】C
【分析】由于AB∥CD，则∠ABO＝∠BOD＝40°，利用平角等于得到∠BOC＝140°，再根据角平分线定义得到∠BOE＝70°；利用OF⊥OE，可计算出∠BOF＝20°，则∠BOF＝∠BOD，即OF平分∠BOD； 利用OP⊥CD，可计算出∠POE＝20°，则∠POE＝∠BOF； 根据∠POB＝70°−∠POE＝50°，∠DOF＝20°，可知④不正确．
【解析】解：∵AB∥CD，
∴∠ABO＝∠BOD＝40°，
∴∠BOC＝180°−40°＝140°，
∵OE平分∠BOC，
∴∠BOE＝×140°＝70°；所以①正确；
∵OF⊥OE，
∴∠EOF＝90°，
∴∠BOF＝90°−70°＝20°，
∴∠BOF＝∠BOD，所以②正确；
∵OP⊥CD，
∴∠COP＝90°，
∴∠POE＝90°−∠EOC＝20°，
∴∠POE＝∠BOF； 所以③正确；
∴∠POB＝70°−∠POE＝50°，
而∠DOF＝20°，所以④错误．
故选C．
【点睛】本题考查了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补；两直线平行，同位角相等．也考查了角平分线的定义．
8．为了亮化某景点，石家庄市在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯，如图所示．A灯发出的光束自AM逆时针旋转至AN便立即回转，B灯发出的光束自BP逆时针旋转至BQ便立即回转，两灯不间断照射，A灯每秒转动30°，B灯每秒转动10°，B灯先转动2秒，A灯才开始转动，当B灯光束第一次到达BQ之前，两灯的光束互相平行时A灯旋转的时间是（ ）
A．1或6秒B．8.5秒C．1或8.5秒D．2或6秒
【答案】C
【分析】设灯旋转的时间为秒，求出的取值范围为，再分①，②和③三种情况，先分别求出和的度数，再根据平行线的性质可得，由此建立方程，解方程即可得．
【解析】解：设灯旋转的时间为秒，
灯光束第一次到达所需时间为秒，灯光束第一次到达所需时间为秒，
灯先转动2秒，灯才开始转动，
，即，
由题意，分以下三种情况：
①如图，当时，，
，
，
，
，即，
解得，符合题设；
②如图，当时，，
，
，
，
，即，
解得符合题设；
③如图，当时，，
，
同理可得：，即，
解得，不符题设，舍去；
综上，灯旋转的时间为1秒或秒，
故选：C．
【点睛】本题考查了平行线的性质、一元一次方程的几何应用等知识点，正确求出时间的取值范围，并据此分三种情况讨论是解题关键．
9．①如图1，ABCD，则∠A＋∠E＋∠C＝180°；②如图2，ABCD，则∠E＝∠A＋∠C；③如图3，ABCD，则∠A＋∠E－∠1＝180°；④如图4，ABCD，则∠A＝∠C＋∠P．以上结论正确的个数是（ ）

A．①②③④B．①②③C．②③④D．①②④
【答案】C
【分析】①过点E作直线，由平行线的性质即可得出结论；
②过点E作直线，由平行线的性质即可得出结论；
③过点E作直线，由平行线的性质可得出∠A+∠E-∠1=180°；
④先过点P作直线，再根据两直线平行，内错角相等和同位角相等即可作出判断．
【解析】解：①过点E作直线，
∵，∴，∴∠A＋∠1＝180°，∠2＋∠C＝180°，
∴∠A＋∠C＋∠AEC＝360°，故①错误；
②过点E作直线，
∵，
∴，∴∠A＝∠1，∠2＝∠C，
∴∠AEC＝∠A＋∠C，即∠AEC＝∠A＋∠C，故②正确；
③过点E作直线，
∵，∴，∴∠A＋∠3＝180°，∠1＝∠2，
∴∠A＋∠AEC－∠2＝180°，即∠A＋∠AEC－∠1＝180°，故③正确；
④如图，过点P作直线，
∵，∴，
∴∠1=∠FPA，∠C=∠FPC，
∵∠FPA=∠FPC+∠CPA，
∴∠1＝∠C＋∠CPA，
∵AB∥CD，∴∠A＝∠1，即∠A＝∠C+∠CPA，故④正确．
综上所述，正确的小题有②③④．
故选：C．
【点睛】本题考查的是平行线的性质及平行公理的推论，根据题意作出辅助线是解答此题的关键．
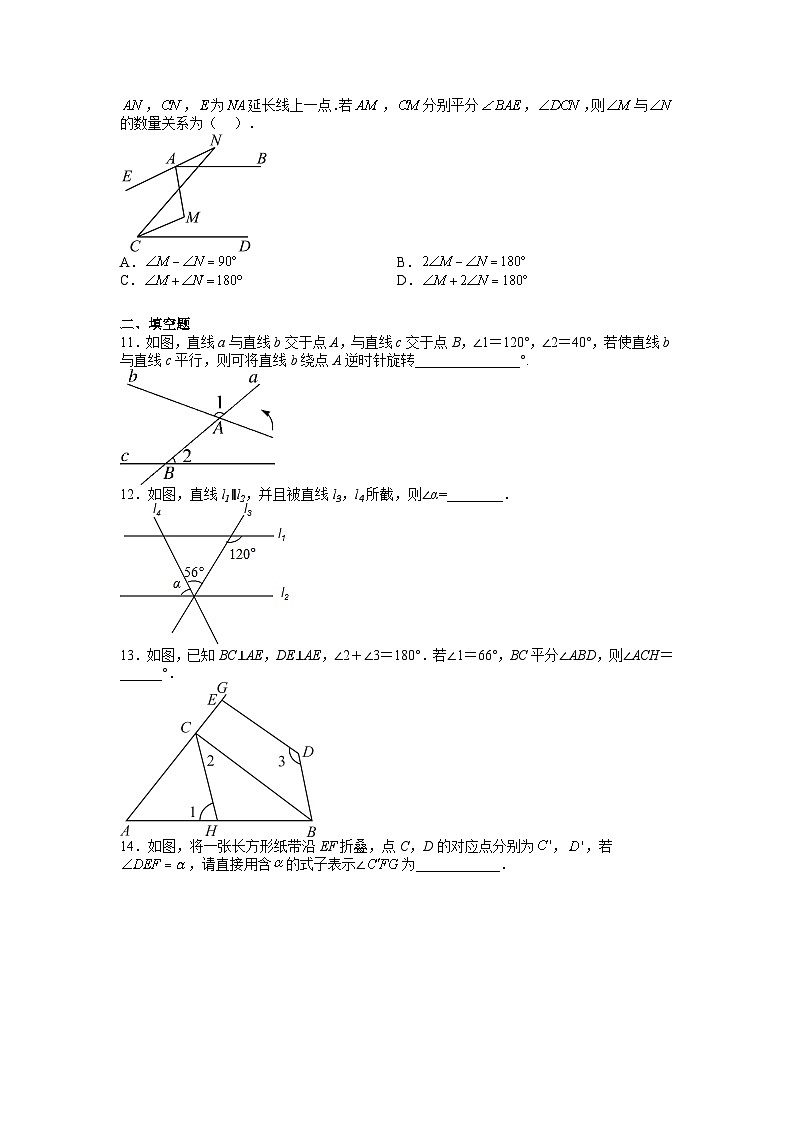
10．如图，已知，为平行线之间一点连接，，为上方一点，连接，，为延长线上一点．若，分别平分，，则与的数量关系为（ ）．
A．B．
C．D．
【答案】B
【分析】过点作，过点作，则，根据平行线的性质可得，，，即可得出结论．
【解析】解：过点作，过点作，
，
，
，，
，分别平分，，
，，，
，
，
，
，
，
，
，
，
故选：B．
【点睛】本题考查了平行线的性质，邻补角的定义，解题的关键是熟练掌握平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
二、填空题
11．如图，直线a与直线b交于点A，与直线c交于点B，∠1＝120°，∠2＝40°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转_______________°.
【答案】20
【分析】根据同位角相等，两直线平行推出即可．
【解析】如图,旋转到直线b′，
∵∠1=120，
∴∠DAE=180−120=60，
∵∠EAC=20，
∴∠DAC=60−20=40，
∵∠2=40，
∴∠2=∠DAC，
∴直线c∥直线b′，
即当直线b绕点A逆时针旋转20时，直线b与直线c平行，
故答案为20.
【点睛】本题考查的知识点是平行线的判定及旋转的性质，解题的关键是熟练的掌握平行线的判定及旋转的性质.
12．如图，直线l1∥l2，并且被直线l3，l4所截，则∠α=________．
【答案】64°
【分析】首先根据三角形外角的性质，求出的度数是多少；然后根据直线，可得，据此求出的度数是多少即可．
【解析】解：如图1，
，
，
，
又直线，
．
故答案为：．
【点睛】此题主要考查了平行线的性质，外角，解题的关键是掌握平行线的性质．
13．如图，已知BC⊥AE，DE⊥AE，∠2＋∠3＝180°．若∠1＝66°，BC平分∠ABD，则∠ACH＝______°．
【答案】57
【分析】根据角平分线得出∠HBC=∠DBC=，根据垂直得出BC∥DE，得出∠3+∠DBC=180°，结合∠2＋∠3＝180°，得出∠DBC=∠3，证出CH∥BD即可．
【解析】解：∵BC平分∠ABD，
∴∠HBC=∠DBC=，
∵BC⊥AE，DE⊥AE，
∴BC∥DE，
∴∠3+∠DBC=180°，
∵∠2＋∠3＝180°，
∴∠DBC=∠2，
∴CH∥BD，
∴∠DBA=∠1=66°，
∴∠DBC=∠2=，
∴∠ACH=∠ACB-∠2=90°-33°=57°．
故答案为：57．
【点睛】本题考查角平分线有关的计算，平行线判定与性质，求余角，掌握角平分线有关的计算，平行线判定与性质，余角性质是解题关键．
14．如图，将一张长方形纸带沿EF折叠，点C，D的对应点分别为，，若，请直接用含的式子表示∠为____________．
【答案】
【分析】由折叠的性质可得：∠DEG＝2α，∥，由AD∥BC可得∠＝∠DEG＝2α，从而有∠＝180°−∠，即可得出结果．
【解析】解：由长方形纸带ABCD及折叠性质可得：∠＝∠DEF＝α，∥，
∴∠DEG＝2∠DEF＝2α，∠＝180°−∠，
∵AD∥BC，
∴∠＝∠DEG＝2α，
∴∠＝180°−2α．
故答案为：180°−2α．
【点睛】本题主要考查平行线的性质，折叠的性质，解答的关键是熟记折叠的性质．
15．如图，已知，，，则________度．
【答案】120
【分析】过E作一条直线，根据题意，得；根据平行线同旁内角互补的性质，推导得，再根据平行线内错角相等的性质计算，即可得到答案．
【解析】解：过E作一条直线，
∵，，
∴，
∵，，
∴，
∴
又∵，
∴．
故答案为：120．
【点睛】本题考查了平行线的知识；解题的关键是熟练掌握平行线的性质，从而完成求解．
16．如图，已知AD∥CE，∠BCF＝∠BCG，CF与∠BAH的平分线交于点F，若∠AFC的余角等于2∠ABC的补角，则∠BAH的度数是______．
【答案】60°##60度
【分析】设∠BAF＝x°，∠BCF＝y°，由题意知∠HAF＝∠BAF＝x°，∠BCG＝∠BCF＝x°，∠BAH＝2x°，∠GCF＝2y°，如图，过点B作BM∥AD，过点F作FN∥AD，由AD∥CE可得AD∥FN∥BM∥CE，有∠AFN＝∠HAF＝x°，∠CFN＝∠GCF＝2y°，ABM＝∠BAH＝2x°，∠CBM＝∠GCB＝y°，∠AFC＝（x+2y）°，∠ABC＝（2x+y）°由于∠F的余角等于2∠B的补角，可知90﹣（x+2y）＝180﹣2（2x+y），进行求解可得x的值，进而可求出∠BAH的值．
【解析】解：设∠BAF＝x°，∠BCF＝y°
∵∠BCF＝∠BCG，CF与∠BAH的平分线交于点F
∴∠HAF＝∠BAF＝x°，∠BCG＝∠BCF＝x°，∠BAH＝2x°，∠GCF＝2y°，
如图，过点B作BM∥AD，过点F作FN∥AD
∵AD∥CE
∴AD∥FN∥BM∥CE
∴∠AFN＝∠HAF＝x°，∠CFN＝∠GCF＝2y°，∠ABM＝∠BAH＝2x°，∠CBM＝∠GCB＝y°
∴∠AFC＝（x+2y）°，∠ABC＝（2x+y）°
∵∠AFC的余角等于2∠ABC的补角
∴90﹣（x+2y）＝180﹣2（2x+y）
解得：x＝30
∴∠BAH＝60°
故答案为：60°．
【点睛】本题考查了角平分线，平行线的性质，余角、补角等知识．解题的关键在于正确的表示角度之间的数量关系．
17．一副直角三角板叠放如图所示，现将含角的三角板固定不动，把含角的三角板由图所示位置开始绕点逆时针旋转且，使两块三角板至少有一组边平行．如图时，．
请你在图、图、图内，各画一种符合要求的图形，标出，并完成各项填空：
图中_______________时，___________//___________﹔图中_____________时，___________//___________﹔图中_______________时，___________//___________﹔
【答案】；（答案不唯一)
【分析】画出图形，再由平行线的判定与性质求出旋转角度．
【解析】图中，当时，DE//AC；
图中，当 时，CE//AB，
图中，当 时，DE//BC．
故答案为：；（答案不唯一）．
【点睛】考查了平行线的判定和性质，解题关键是理解平行线的判定与性质，并且利用了数形结合．
18．已知，点、分别为、上的点，点、、为、内部的点，连接、、、、、，于，，，平分，平分，则（小于平角）的度数为______．
【答案】
【分析】过点，做平行于，根据平行线的传递性及性质得，同理得出，令，则，，则，通过等量关系先计算出，再根据角平分线的性质及等量代换进行求解．
【解析】解：过点，做平行于，如下图：
，
，
则，
，
同理可得：，
令，则，
，则，
则，
，
，
，
平分，平分，
，
，
故答案是：．
【点睛】本题考查了平行线的性质、角平分线的性质，解题的关键是添加适当的辅助线，找到角之间的关系，利用等量代换的思想进行计算求解．
三、解答题
19．如图所示，已知∠1＝50°，∠2＝130°，∠4＝50°，∠6＝130°，试说明a∥b，b∥c，d∥e，a∥c．
【答案】详见解析
【分析】由条件可分别得到∠1+∠2=180°，可证明a∥b；可求得∠4=∠3，可证明d∥e；由∠5+∠6=180°可求得∠4=∠5，可证明b∥c，由平行的传递性可得a∥c．
【解析】因为∠1＝50°，∠2＝130°(已知)，
所以∠1+∠2＝180°．
所以a∥b(同旁内角互补，两直线平行)．
所以∠3＝∠1＝50°(两直线平行，同位角相等)．
又因为∠4＝50°(已知)，
所以∠3＝∠4(等量代换)．
所以d∥e(同位角相等，两直线平行)．
因为∠5+∠6＝180°(平角定义)，∠6＝130°(已知)，
所以∠5＝50°(等式的性质)．
所以∠4＝∠5(等量代换)．
所以b∥c(内错角相等，两直线平行)．
因为a∥b，b∥c(已知)，
所以a∥c(平行于同一直线的两直线平行)．
【点睛】本题主要考查平行线的判定，掌握平行线的判定和性质是解题的关键，即①同位角相等⇔两直线平行，②内错角相等⇔两直线平行，③同旁内角互补⇔两直线平行，④a∥b，b∥c⇒a∥c．
20．将下列证明过程及依据补充完整．
如图，在中，平分交于点D，E，F分别为，上的点，且，，求证：平分
证明：∵平分（已知），
∴（角平分线的定义）．
∵（已知），
∴（ ）
∴（等量代换），
∵（已知），
∴（ ）
（ ）
∴_____=______（等量代换），
∴平分（ ）
【答案】两直线平行，内错角相等；两直线平行，内错角相等；两直线平行，同位角相等；；；角平分线的定义．
【分析】根据平行线的性质和角平分线的概念求解即可．
【解析】证明：∵平分（已知），
∴（角平分线的定义）．
∵（已知），
∴（两直线平行，内错角相等）
∴（等量代换），
∵（已知），
∴（两直线平行，内错角相等）
（两直线平行，同位角相等）
∴=（等量代换），
∴平分（角平分线的定义）
故答案为：两直线平行，内错角相等；两直线平行，内错角相等；两直线平行，同位角相等；；；角平分线的定义．
【点睛】本题考查了平行线的性质和平行线的判定在几何证明中的应用，明确相关性质及定理是解题的关键．
21．已知：如图，直线，直线MN交EF，PO于点A，B，直线HQ交EF，PO于点D，C，DG与OP交于点G，若，，．
（1）求证：；
（2）请直接写出的度数．
【答案】（1）见解析；（2）
【分析】（1）根据可得，，再根据内错角相等两直线平行即可得证；
（2）根据两直线平行的性质可得，从而可得，再由即可求解．
【解析】解：（1）∵，
∴，
∵，
∴，
∴；
（2）∵，，
∴，
，
∵，
∴，
∴．
【点睛】本题考查了平行线的判定及性质，解题的关键是掌握平行线的判定及性质，利用数形结合的思想进行求解．
22．如图，平分，.
（1）求证：//；
（2）若，，求的度数（用含的代数式表示）.
【答案】（1）见解析；（2）
【分析】（1）利用内错角相等，两直线平行证明即可；
（2）根据平行线的性质求出∠ABC的度数，再根据角平分线的性质得到∠3的度数，再由平行线的性质可求出结果.
【解析】（1）证明：∵平分，
∴．
∵，
∴．
∴∥．
（2） ∵∥且，
∴．
∴．
同理可证：．
∵，
∴．
∴
=
=．
【点睛】此题主要考查了平行线的判定与性质，熟练掌握判定定理和性质定理是解决此题的关键.
23．如图是由100个边长为1的小正方形组成的网格，线段的两端都在小正方形的顶点，请按要求画图并解决问题：
(1)将线段平移到线段（点A与点C对应），画出线段；
(2)连接，直接写出与之间的数量关系与位置关系；
(3)连接，的面积为______________．
【答案】(1)作图见解析
(2)作图见解析，AC＝BD，ACBD；
(3)图见解析，的面积为13
【分析】（1）利用平移变换的性质作出点B的对应点D，即可；
（2）利用平移变换的性质判断即可；
（3）把三角形的面积看成长方形的面积减去周围的三个三角形面积即可．
（1）
解：如图，线段CD即为所求；
（2）
如图，AC＝BD，ACBD；
（3）
△ABC的面积＝5×63×42×62×5＝13，
故答案为：13．
【点睛】本题考查作图﹣平移变换，三角形的面积等知识，解题的关键是熟练掌握平移变换的性质，属于常考题型．
24．已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置跳到终点位置有两种不同路径，路径1：；路径2：.
试一试：（1）写出从起始位置跳到终点位置的一种路径；
（2）从起始位置依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置？
【答案】（1）（答案不唯一）；（2）能跳到终点位置.其路径为
（答案不唯一）
【分析】（1）根据同旁内角、内错角和同位角的定义进行选择路径即可；
（2）先判断能够到达终点位置，在根据定义给出具体路径即可.
【解析】（1）可以是这样的路径：.（答案不唯一）
（2）从起始位置依次按同位角内错角同旁内角的顺序跳，能跳到终点位置.其路径为
（答案不唯一）.
【点睛】本题考查的是同位角、内错角和同旁内角的定义，熟知这些角的特征是解题的关键.
25．已知，点A在上，的两边与相交于点B，与相交于点C，平分．
(1)如图1，若，，的数量关系为 ；
(2)如图2，在（1）的条件下，若，，求证；
(3)点B、C分别在点D、E的下方，若，，请在备用图中画出相应的图形，并求出的度数．
【答案】(1)
(2)证明见解析
(3)
【分析】（1）由两直线平行内错角相等可得，再根据平分的性质即可推出数量关系；
（2）由得到，再由结合可列出，求得，从而得到，此题得证；
（3）设，根据题意得，，再根据列方程并解出，最后根据余角性质求出，此题得解．
【解析】（1），
证明：∵，平分，
∴，，
∴；
（2）证明：∵，∴，
∵，，，
平分，，
∴，，
∴，
∴与都相交于直线上的A点，
并且在同一平面内，，
∴；
（3）证明：设，则，
，，
，解得
．
【点睛】本题考查了平行线的性质和角平分线的性质的综合题，熟练和灵活运用其性质建立好等量关系是解决本题的关键．
26．已知，直角的边与直线a分别相交于O、G两点，与直线b分别交于E、F点，．
（1）将直角如图1位置摆放，如果，则______；
（2）将直角如图2位置摆放，N为AC上一点，，请写出与之间的等量关系，并说明理由．
（3）将直角如图3位置摆放，若，延长AC交直线b于点Q，点P是射线GF上一动点，探究，与的数量关系，请直接写出结论．
【答案】（1）136°；（2）∠AOG+∠NEF＝90°，理由见解析；（3）当点P在GF上时，∠OPQ＝140°﹣∠POQ+∠PQF；当点P在线段GF的延长线上时，140°﹣∠POQ＝∠OPQ+∠PQF．
【分析】（1）如图1，作CP∥a，则CP∥a∥b，根据平行线的性质可得∠AOG＝∠ACP，∠BCP+∠CEF＝180°，然后利用∠ACP+∠BCP＝90°即可求得答案；
（2）如图2，作CP∥a，则CP∥a∥b，根据平行线的性质可得∠AOG＝∠ACP，∠BCP+∠CEF＝180°，然后结合已知条件可得∠BCP＝∠NEF，然后利用∠ACP+∠BCP＝90°即可得到结论；
（3）分两种情况，如图3，当点P在GF上时，过点P作PN∥OG，则NP∥OG∥EF，根据平行线的性质可推出∠OPQ＝∠GOP+∠PQF，进一步可得结论；如图4，当点P在线段GF的延长线上时，同上面方法利用平行线的性质解答即可．
【解析】解：（1）如图1，作CP∥a，
∵，
∴CP∥a∥b，
∴∠AOG＝∠ACP，∠BCP+∠CEF＝180°，
∴∠BCP＝180°﹣∠CEF，
∵∠ACP+∠BCP＝90°，
∴∠AOG+180°﹣∠CEF＝90°，
∵∠AOG＝46°，
∴∠CEF＝136°，
故答案为136°；
（2）∠AOG+∠NEF＝90°．
理由如下：如图2，作CP∥a，
则CP∥a∥b，
∴∠AOG＝∠ACP，∠BCP+∠CEF＝180°，
而∠NEF+∠CEF＝180°，
∴∠BCP＝∠NEF，
∵∠ACP+∠BCP＝90°，
∴∠AOG+∠NEF＝90°；
（3）如图3，当点P在GF上时，过点P作PN∥OG，
∴NP∥OG∥EF，
∴∠GOP＝∠OPN，∠PQF＝∠NPQ，
∴∠OPQ＝∠GOP+∠PQF，
∴∠OPQ＝140°﹣∠POQ+∠PQF；
如图4，当点P在线段GF的延长线上时，过点P作PN∥OG，
∴NP∥OG∥EF，
∴∠GOP＝∠OPN，∠PQF＝∠NPQ，
∵∠OPN＝∠OPQ+∠QPN，
∴∠GOP＝∠OPQ+∠PQF，
∴140°﹣∠POQ＝∠OPQ+∠PQF．
【点睛】本题考查了平行线的性质以及平行公理的推论等知识，属于常考题型，正确添加辅助线、灵活应用平行线的判定和性质是解题的关键．
27．【感知】如图①， ， ，．求的度数．
（提示：过点P作直线）
【探究】如图②，，点P在射线OM上运动， ，．
（1）当点P在线段AB上运动时，，，之间的数量关系为_______________．
（2）当点P在A，B两点外侧运动时（点P与点A，B，O三点不重合），直接写出，， 之间的数量关系为____________________________________________________________．
【答案】【感知】；【探究】（1）；（2）或．
【分析】[感知]根据平行线性质知两直线平行同旁内角互补可以求出，∠APQ和∠CPQ ，
[探究]（1）作，根据两直线平行内错角相等结合等量代换即可得出结论；
（2）分类讨论当P在AM上或OB上时两种情况，分别作平行线结合两直线平行内错角相等进行求证即可．
【解析】解：[感知]过点P作直线，
∵，
∴．
∴，，
∵，，
∴，，
∴．
∴的度数为．
[探究]（1）．
如图②：作，
∵，
∴，
∴∠DPQ=∠，∠CPQ=∠ ，
∴；
（2）或．
如图③：当P在AM上时，作，
∵，
∴，
∴∠DPQ=∠，∠CPQ=∠ ，
∴；
当P在OB上时，同理：．
综上所述，或．
【点睛】此题主要考查平行线的性质：两直线平行，内错角相等，同旁内角互补等结合等量代换进行证明，做辅助线进行转化是关键．