高中数学第三章 函数的概念与性质3.2 函数的基本性质第2课时教学设计

这是一份高中数学第三章 函数的概念与性质3.2 函数的基本性质第2课时教学设计，共9页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
第2课时 函数的最大（小）值

一、教学目标
1.结合函数单调性和图象理解函数的最大（小）值概念的含义，培养学生数学抽象的核心素养；
2.让学生经历通过判断函数的单调性求函数最值的过程，培养学生严谨的思维习惯，提升逻辑推理的核心素养;
3.通过应用函数最值解决实际问题，培养学生的应用意识，提高学生发现问题、解决问题的能力.

二、教学重难点
重点: 理解函数的最大（小）值的含义.
难点：能够通过函数图象或者函数单调性求得函数的最值.

三、教学过程
（一）创设情境
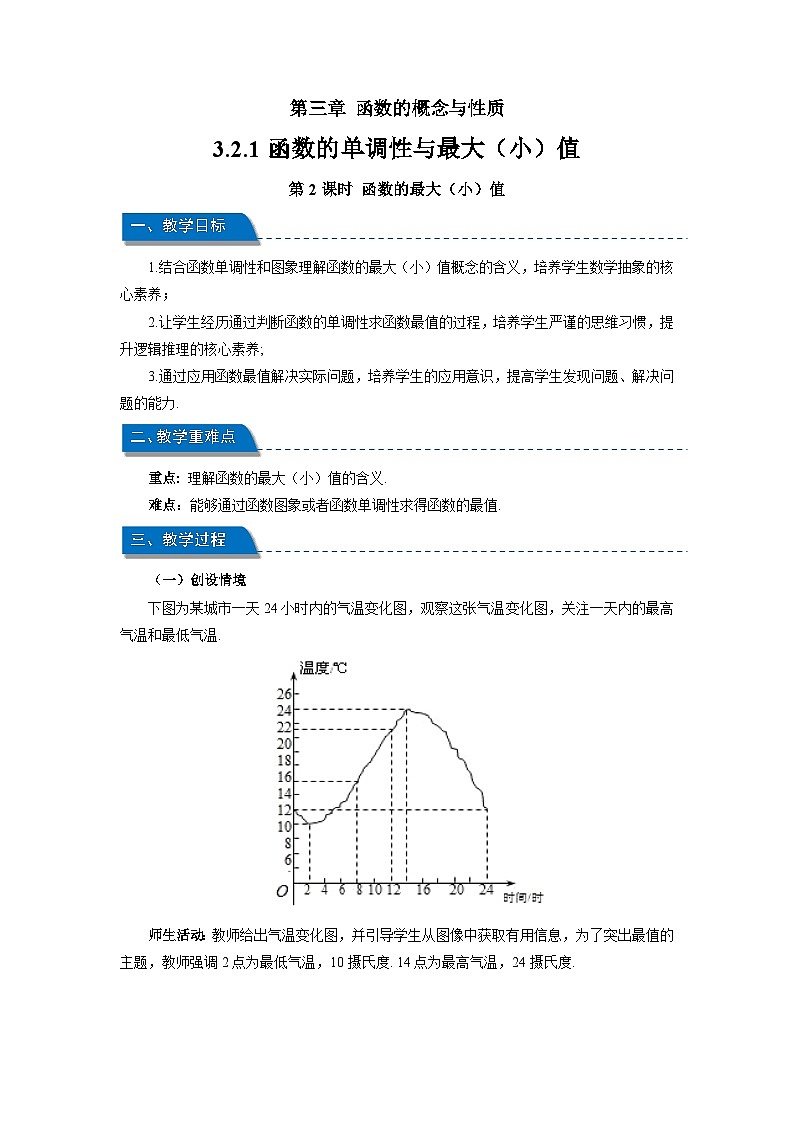
下图为某城市一天24小时内的气温变化图，观察这张气温变化图，关注一天内的最高气温和最低气温.
师生活动：教师给出气温变化图，并引导学生从图像中获取有用信息，为了突出最值的主题，教师强调2点为最低气温，10摄氏度. 14点为最高气温，24摄氏度.
设计意图：使学生体会到生活中处处有数学，数学就在我们身边，我们生活在充满数学信息的现实世界中. 能促进学生会用数学的眼光去观察和认识周围的事物，有效的促进知识的迁移.
（二）探究新知
任务1：函数的最小值.
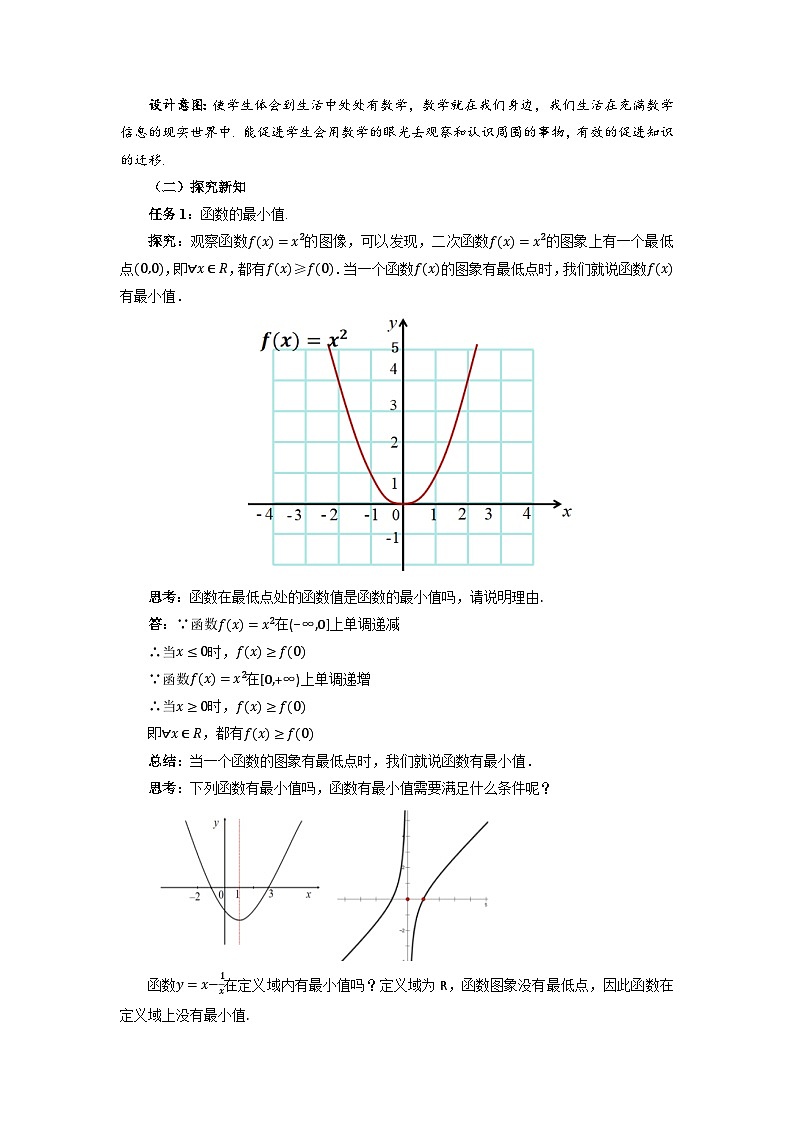
探究：观察函数f(x)=x2的图像，可以发现，二次函数f(x)=x2的图象上有一个最低点(0,0)，即∀x∈R，都有f(x)≥f(0)．当一个函数f(x)的图象有最低点时，我们就说函数f(x)有最小值．
思考：函数在最低点处的函数值是函数的最小值吗，请说明理由.
答：∵函数f(x)=x2在(−∞,0]上单调递减
∴当x≤0时，f(x)≥f(0)
∵函数f(x)=x2在[0,+∞)上单调递增
∴当x≥0时，f(x)≥f(0)
即∀x∈R，都有f(x)≥f(0)
总结：当一个函数的图象有最低点时，我们就说函数有最小值．
思考：下列函数有最小值吗，函数有最小值需要满足什么条件呢？
函数y=x−1x在定义域内有最小值吗？定义域为R，函数图象没有最低点，因此函数在定义域上没有最小值.
函数y=x2−2x−3在[−2,2]内有最小值吗？函数在区间上的图象有最低点，因此函数在区间上有最小值.
思考：函数有最小值需要满足什么条件呢？函数最小值的定义是怎样的呢？
答：函数有最小值应满足的条件：
函数在整个定义域或某个区间内，函数图象有最低点，就说函数在定义域内或某区间内有最小值.
【概念形成】
函数的最小值：一般地，设函数y=f(x)的定义域为I，如果存在实数M满足：
(1)∀x∈I，都有f(x)≥M；
(2)∃x0∈I，使得f(x0)=M.
那么，我们称M是函数y=f(x)的最小值.
思考：函数最小值定义中的条件(2)可以省略吗？为什么？
答：不可以省略，因为要保证可以取到最小值.
任务2：函数的最大值
探究：观察二次函数f(x)=−x2的图象，可以发现，二次函数f(x)=−x2的图象上有一个最高点，即点(0,0). ∀x∈R，都有f(x)≤f(0)．
思考：(1)函数在最高点处的函数值是函数的最大值吗？
(2)函数图象具有怎样的特征时，函数具有最大值？
(3)你能归纳出函数最大值的定义吗？
答：(1)是函数的最大值.
(2)当一个函数的图象有最高点时，我们就说函数有最大值．
【概念形成】
函数的最大值：一般地，设函数y=f(x)的定义域为I，如果存在实数M满足：
(1)∀x∈I，都有f(x)≤M；
(2)∃x0∈I，使得f(x0)=M.
那么，我们称M是函数y=f(x)的最大值.
思考：一个函数一定有最大值或最小值吗？为什么？
答：不一定. 比如：
一次函数f(x)=kx+b(x∈R)时，无最大值和最小值；
二次函数f(x)=ax2+bx+c(a≠0)（开口向上时有最小值无最大值；开口向下时有最大值无最小值）；
反比例函数f(x)=1x，无最大值和最小值；
常函数f(x)=c（既有最大值又有最小值，且最大值和最小值相等）.
对于给定区间的函数，看区间端点能否取到，具体情况具体分析.
师生活动：教师结合二次函数图像引入函数的最大值、最小值，给出函数的最大值概念，引导学生形成函数的最小值概念.
设计意图：通过第一课时实例函数的引入，让学生开始关注函数的最值.
任务3：探究函数最值在实际问题中的应用
探究：“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度ℎ(单位：m)与时间t(单位：s)之间的关系为ℎ(t)=−4.9t2+14.7t+18，那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少？(精确到1m)?
提示：爆裂的最佳时刻是指烟花冲到最高点的时刻，此时高度是函数的最大值.
解：画出函数ℎ(t)=−4.9t2+14.7t+18的图象.显然，函数图象的顶点就是烟花上升的最高点，顶点的横坐标就是烟花爆裂的最佳时刻，纵坐标就是这时距地面的高度．
由二次函数的知识，对于函数h(t)=−4.9t2+14.7t+18，我们有：
当t =−14.72×(−4.9)=1.5时，函数有最大值h=4×(−4.9)×18−14.724×(−4.9)≈29．
于是，烟花冲出后1.5s是它爆裂的最佳时刻，这时距地面的高度约为29m．
总结：图像法求函数最值的一般步骤：
作出函数图象；在图象上找到最高点或最低点对应的横纵坐标；确定函数的最大(小)值.
总结：函数最值的应用：
解实际应用题时，要弄清题意，从实际出发，引入数学符号，建立数学模型，列出函数关系式，分析函数的性质，从而解决问题，要注意自变量的取值范围.
在实际应用问题中，最大利润、用料最省等问题常转化为求函数最值来解决，本题转化为二次函数求最值，利用配方法和分类讨论思想使问题得到解决.
师生活动：教师提出图象法求解函数最值并给出例题，在学生思考作答后讲解.
设计意图：让学生学习图象法求解函数最值的方法.
任务4：借助函数的单调性求解函数的最值.
探究：已知函数f(x)=2x−1(x∈[2,6])，求函数的最大值和最小值．
思考：函数的最大值、最小值是在端点处取到吗？
答：如果函数在所给闭区间上是单调函数，则可以在端点处取得函数在闭区间上的最大值和最小值. 所以需要先证明函数的单调性，再求得函数的最值.
解：∀x1，x2∈[2,6]，且x10，于是f(x1)−f(x2)>0，即f(x1)>f(x2).
所以，函数f(x)=2x−1在区间[2,6]上单调递减．
因此，函数f(x)=2x−1在区间[2,6]的两个端点上分别取得最大值与最小值.在x=2时取得最大值，最大值是2;
在x=6时取得最小值，最小值是0.4．
总结：（1）若函数y=f(x)在区间[a,b]上单调递增，则f(x)的最大值为f(b)，最小值为f(a).
（2）若函数y=f(x)在区间[a,b]上单调递减，则f(x)的最大值为f(a)，最小值为f(b).
（3）若函数y=f(x)在区间[a,b]上有增有减，则先求出每个单调区间的最值，再从各个单调区间中的最大值中选出最大的作为f(x)的最大值，从各个单调区间中的最小值中选出最小的作为f(x)的最小值.
师生活动：教师提出函数最值的求解可以通过函数单调性求解，并给出例题，在学生思考作答后讲解. 总结闭区间上单调函数的最值情况.
设计意图：让学生学会利用单调性求解函数的最值.
任务5：恒成立、存在有解问题.
探究：∀x∈[0,2]，x2>2x−a恒成立，求a的范围.
解：问题转化为∀x∈[0,2]，a>−x2+2x恒成立.
记f(x)=−x2+2x,x∈[0,2]. 只需a>f(x)max.
f(x)max=1，a>1.
总结：∀x∈D,a≥f(x)恒成立，能推出a≥f(x)max,x∈D
∀x∈D,a≤f(x)恒成立，能推出a≤f(x)min,x∈D
∃x∈D,a≥f(x)，能推出a≥f(x)min,x∈D
∃x∈D,a≤f(x)，能推出a≤f(x)max,x∈D
（三）应用举例
例1：设函数f(x)的定义域为[−6,11].如果f(x)在区间[−6,−2]上单调递减，在区间[−2,11]上单调递增，画出f(x)的一个大致的图象，从图象上可以发现f(−2)是函数f(x)的一个 ．
解：由题意画出函数的图象，可知发现f(−2)是函数f(x)的一个最小值，
故答案为：最小值．
例2：设函数fx=x+2x−1．
(1)用函数单调性定义证明：函数fx在区间1,+∞上是单调递减函数；
(2)求函数fx在区间3,5上的最大值和最小值．
解：(1)证明：设x2>x1>1，
由题有fx1−fx2=x1+2x1−1−x2+2x2−1=3x2−x1x1−1x2−1，
∵x2>x1>1，
∴x2−x1>0，x1−1>0，x2−1>0，
∴fx1−fx2>0，即fx1>fx2，
∴函数fx在区间1,+∞上是单调递减函数．
(2)由(1)可知fx在区间3,5上单调递减，
∴fx的最大值为f3=52，最小值为f5=74．
∴函数fx在区间3,5上的最大值为52，最小值为74．
例3：某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=x25−48x+8 000，已知此生产线年产量最大为210吨．
(1)求年产量为多少吨时，总成本最低，并求最低成本;
(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润?最大利润是多少?
解：(1)因为y=x25−48x+8000=15(x−120)2+5120(0≤x≤210)，
所以当年产量为120吨时，其生产的总成本最低，最低成本为5120万元．
(2)设该工厂年获得总利润为f(x)万元，
则f(x)=40x−y=40x−x25+48x−8000=−x25+88x−8000=−15(x−220)2+1680(0≤x≤210)．
因为f(x)在[0,210]上是增函数，
所以当x=210时，f(x)有最大值为−15(210−220)2+1680=1660．
故当年产量为210吨时，可获得最大利润1660万元．
设计意图：巩固知识，强化理解.
课堂练习
1.函数f(x)=2x−1,x∈[2,6]的值域是( )
A. [13,2]B. [25,2]C. [25,+∞)D. (−∞,2]
解：因为f(x)=2x−1在[2,6]上单调递减，
故当x=2时，函数取得最大值2，当x=6时函数取得最小值25．
故选：B．
2.下列函数中，在其定义域上单调递增且值域为R的是( )
A. y=2xB. y=(x−1)3C. y=x+1xD. y=|lnx|
解：对于A，函数y=2x是定义域R上的增函数，其值域是(0,+∞)，不满足题意；
对于B，函数y=(x−1)3是定义域R上的增函数，且值域是R，满足题意；
对于C，函数y=x+1x是对勾函数，不是定义域(−∞,0)∪(0,+∞)上的增函数，不满足题意；
对于D，函数y=|lnx|不是定义域(0,+∞)上的增函数，不满足题意．
故选：B．
3.已知函数f(x)=x2−2tx+1在区间(−∞,1]上递减，且当x∈[0,t+1]时，有f(x)max−f(x)min⩽2，则实数t的取值范围是( )
A. [− 2, 2]B. [1, 2]C. [2,3]D. [1,2]
解：函数f(x)=x2−2tx+1的对称轴为直线x=t，
因为函数f(x)=x2−2tx+1在区间(−∞,1]上递减，
所以t≥1，
所以当x∈[0,t+1]时，f(x)min=f(t)=t2−2t2+1=1−t2，f(x)max=f(0)=1，
所以1−(1−t2)⩽2，解得− 2⩽t⩽ 2，
因为t≥1，所以1≤t≤ 2，
则实数t的取值范围是[1, 2]．
故选：B．
4.已知函数f(x)=x2−2x−a−2x，a∈R．
(1)当a=3时，求函数f(x)的单调递增区间；
(2)令g(x)=f(x)+x2，若g(x)在x∈[−1,2]的最大值为5，求a的值．
解：(1)当 a=3 时，
f(x)=x2−2x−3−2x=x2−4x−3,x≤−1,x≥33−x2,−1