人教版（2024）八年级上册11.3.2 多边形的内角和教学设计

这是一份人教版（2024）八年级上册11.3.2 多边形的内角和教学设计，共3页。教案主要包含了教学与建议等内容，欢迎下载使用。

●置疑导入 清晨，小明沿一个五边形广场周围的小路，从A点出发，按顺时针方向跑步．
【问题1】小明每从一条小路转到下一条小路，身体转过的角是哪些角？
【问题2】他每跑完一圈，身体转过的角度之和是多少？
【问题3】在右图中，你能求出∠1＋∠2＋∠3＋∠4＋∠5的度数吗？
【教学与建议】教学：通过生活中的实际问题及提问设疑，调动学生的学习兴趣和注意力．建议：教师要充分调动学生学习的积极性，把生活中的问题转化为数学问题．
●类比导入 【问题1】三角形的内角和等于多少度？长方形的内角和等于多少度？正方形的内角和等于多少度？
【问题2】长方形和正方形是特殊的四边形，其内角和是360°，任意四边形的内角和等于多少度？
【问题3】你是怎样得到的？你能找到几种方法？
eq \(\s\up7(),\s\d5(\a\vs4\al(分割成2个三角形,180°×2＝360°))) eq \(\s\up7(),\s\d5(\a\vs4\al(分割成3个三角形,180°×3－180°＝360°))) eq \(\s\up7(),\s\d5(\a\vs4\al(分割成3个三角形,180°×3－180°＝360°))) eq \(\s\up7(),\s\d5(\a\vs4\al(分割成4个三角形,180°×4－360°＝360°)))
【问题4】对比观察这些分法有什么异同点．
【问题5】选一种你喜欢的上述分割的方法，求出五边形、六边形、七边形的内角和．
【问题6】n边形的内角和怎样表示呢？
【教学与建议】教学：从四边形入手，利用三角形的内角和是180°转化探索多边形的内角和．建议：分组探究，教师及时了解学生探索的情况．
命题角度1 利用多边形的内角和公式计算
根据多边形内角和公式(n－2)×180°可求角度，建立方程可求边数．
【例1】一个六边形的内角和为(A)
A．720° B．540° C．360° D．450°
【例2】一个n边形的内角和是1 800°，则n＝__12__．
命题角度2 利用多边形的外角和计算
多边形的外角和恒为360°.
【例3】已知正多边形的一个外角等于30°，那么这个正多边形的边数为(D)
A．11 B．10 C．9 D．12
【例4】正十边形的每个外角度数是__36°__．
【例5】正八边形的每个外角都等于__45__度．
命题角度3 多边形的内角和、外角和的应用
从物体形状中抽象得到多边形，应用多边形内角和公式、外角和性质解决实际问题．
【例6】如图，小华从点A出发，沿直线前进12 m后向左转24°，再沿直线前进12 m，又向左转24°……照这样走下去，他第一次回到出发地点A时，一共走的路程是(C)
A.144 m B．120 m
C．180 m D．240 m
命题角度4 多边形的内角和与外角和的综合运用
先设此多边形的边数为n，再根据多边形的内角和以及外角和建立关于边数的方程．
【例7】正多边形的一个外角是36°，则这个正多边形的内角和是__1__440°__．
【例8】若一个正多边形的一个内角是与其相邻外角的4倍，则这个正多边形的边数是__10__．
命题角度5 常见的星形角度的求和问题
求星形角度的和时，一般要构造多边形，把问题变为求多边形的内角和运算.
【例9】如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＝__720°__．
eq \(\s\up7(),\s\d5(（例9题图）)) eq \(\s\up7(),\s\d5(（例10题图）))
【例10】如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＝__540°__.
高效课堂 教学设计
1．通过不同方法探索多边形的内角和与外角和公式．
2．学会运用多边形的内角和与外角和公式进行有关计算．
▲重点
多边形的内角和公式及外角和．
▲难点
多边形内角和公式的推导及其运用．
◆活动1 新课导入
1．我们知道三角形的内角和为__180°__．
2．我们还知道，正方形的四个角都等于90°，那么它的内角和为__360°__，同样长方形的内角和也是360°.
3．正方形和长方形都是特殊的四边形，其内角和为360°，那么一般的四边形的内角和为多少呢？多边形的内角和又是多少呢？
◆活动2 探究新知
1．教材P21 思考及P22例1上面的内容．
提出问题：
(1)我们知道三角形的内角和等于180°，正方形、长方形的内角和都等于360°，那么任意一个四边形的内角和是否也等于360°呢？
(2)如何证明四边形的内角和等于360°？
(3)通过类比，你能推出五边形、六边形的内角和吗？
(4)从n边形的一个顶点出发，可以作几条对角线？它们将n边形分成几个三角形？
(5)如何推导多边形的内角和？多边形的内角和与边数有什么关系？
学生完成并交流展示．
2．教材P22 例2.
提出问题：
(1)在六边形的每个顶点处有几个外角？它们之间有什么关系？每个外角与它相邻的内角之间有什么关系？
(2)你能求出六边形的外角和吗？六边形的外角和与它的边数有什么关系？
(3)如果把六边形改为七边形、八边形等，你能求出它们的外角和吗？
学生完成并交流展示．
3．教材P23 思考．
提出问题：
(1)在一个多边形中，任何一个外角与它相邻的内角有什么关系？
(2)多边形的内角和与外角和有什么关系？
(3)三角形的外角和是360°，多边形的外角和也是360°吗？
(4)n(n≥3)边形的外角和与它的边数有没有关系？
(5)你能用其他方法解释一下多边形的外角和为什么等于360°吗？
学生完成并交流展示．
◆活动3 知识归纳
1．多边形的内角和等于__(n－2)×180°__．
2．多边形的外角和等于__360°__．
提出问题：你还能用其他方法推导多边形的内角和公式吗？试试看．
强调：n边形的外角和为一定值，与它的边数无关．
◆活动4 例题与练习
例1 已知一个多边形的内角和与外角和之比为7∶2，求这个多边形的边数.
解：设多边形的边数为n，由题意，得 eq \f(（n－2）×180°,360°) ＝ eq \f(7,2) ，解得n＝9，即这个多边形的边数为9.
例2 在四边形ABCD中，∠A＝140°，∠D＝80°.
(1)如图①，若∠ABC的平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；
(2)如图②，若∠ABC和∠BCD的平分线交于点E，试求出∠BEC的度数．
解：(1)∵BE∥AD，∴∠A＋∠ABE＝180°，即140°＋∠ABE＝180°，∴∠ABE＝40°.∵BE平分∠ABC，∴∠ABC＝80°.由∠A＋∠ABC＋∠C＋∠D＝360°，得∠C＝360°－140°－80°－80°＝60°；
(2)由已知，得∠EBC＝ eq \f(1,2) ∠ABC，∠ECB＝ eq \f(1,2) ∠BCD.∵∠A＋∠ABC＋∠BCD＋∠D＝360°，∴140°＋2∠EBC＋2∠ECB＋80°＝360°，∴∠EBC＋∠ECB＝70°，∴∠BEC＝110°.
练习
1．教材P24 练习第1，2，3题．
2．若一个多边形的每个内角均为120°，则从此多边形的一个顶点出发可作的对角线的条数为(B)
A．2 B．3 C．4 D．5
3．在四边形ABCD中，若∠A∶∠B∶∠C∶∠D＝3∶1∶2∶3，则该四边形中最大的角的度数是__120°__．
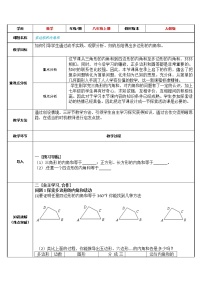
4．如图，小明从点A出发，沿直线前进8 m后左转40°，再沿直线前进8 m，又左转40°，照这样走下去，他第一次回到出发点A时．
(1)整个行走路线是什么图形？
(2)一共走了多少米？
解：(1)因为形成的图形的每条边都相等，每个内角都相等，所以行走路线是正多边形．这个正多边形的边数为360÷40＝9，所以行走路线是正九边形；
(2)8×9＝72(m).
◆活动5 课堂小结
1．多边形的内角和公式．
2．多边形的外角和．
1．作业布置
(1)教材P24～25 习题11.3第2，3，4，5，6题；
(2)对应课时练习．
2．教学反思