
高中人教A版 (2019)7.2 复数的四则运算课时练习
展开典例精讲
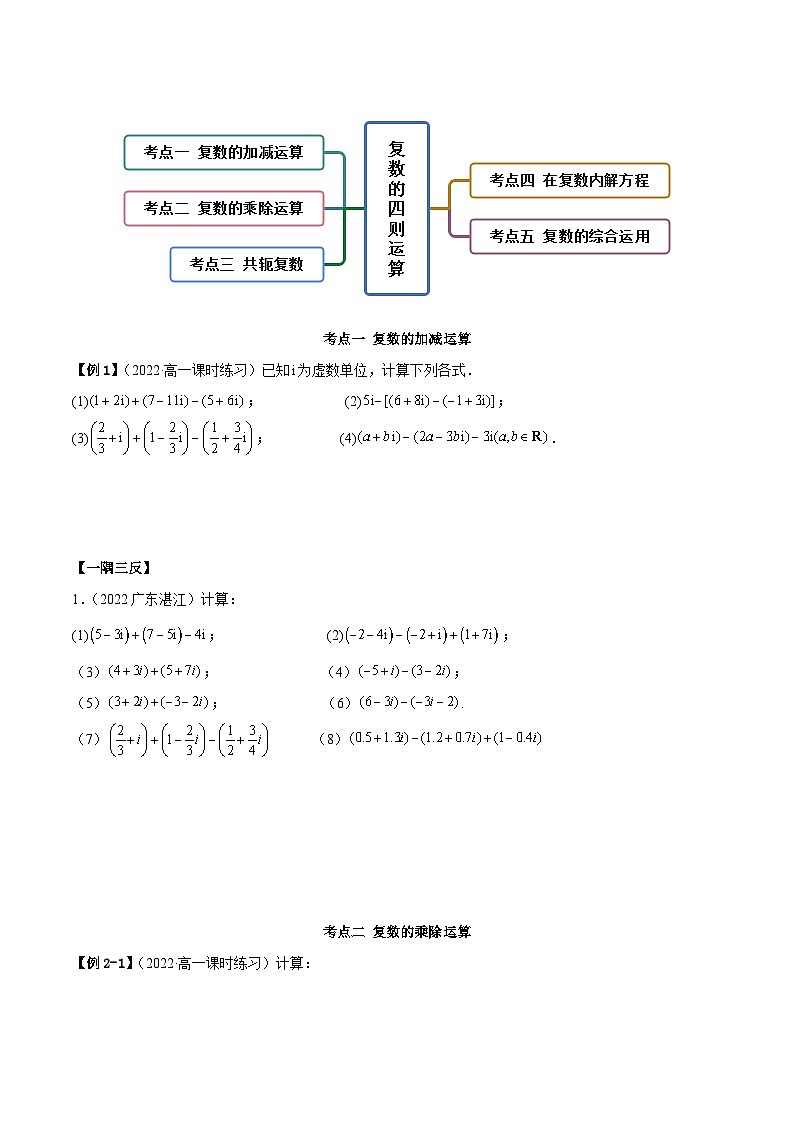
考点一 复数的加减运算
【例1】(2022·高一课时练习)已知为虚数单位,计算下列各式.
(1); (2);
(3); (4).
【一隅三反】
1.(2022广东湛江)计算:
(1); (2);
(3); (4);
(5); (6).
(7) (8)
考点二 复数的乘除运算
【例2-1】(2022·高一课时练习)计算:
(1); (2);
(3); (4).
【例2-2】(2022·高一课时练习)计算:
(1); (2).(3)i+2i2+3i3+…+2 020i2 020+2 021i2 021.
【一隅三反】
1.(2022·全国·高一假期作业)设,则_______.
2.(2023·高一课时练习)______.(其中i是虚数单位)
3(2023·高一课时练习)计算.
(1); (2).
(3); (4);(5).
考点三 共轭复数
【例3】(2022春·吉林长春·高一校考期中)已知复数,则的共轭复数为___________.
【一隅三反】
1.(2022·高一单元测试)已知为虚数单位,复数的共轭复数为( )
A.B.C.D.
2.(2023·全国·高一专题练习)在复平面内,复数(i为虚数单位)的共轭复数对应的点位于( ).
A.第一象限;B.第二象限;C.第三象限;D.第四象限.
3.(2022春·辽宁沈阳·高一沈阳市第四十中学校考阶段练习)已知复数z满足,其中为虚数单位,则z的共轭复数为___________.
考点四 在复数内解方程
【例4-1】(2022·全国·高一专题练习)已知是关于x的方程的根,则实数______.
【例4-2】(2022春·上海浦东新·高一校考期末)已知关于的实系数一元二次方程有两个虚根和,且,则的值为( )
A.2B.C.D.
【例4-3】(2022·高一课时练习)在复数范围内分解因式:
(1);(2).
.
【一隅三反】
1.(2022春·福建泉州·高一校考阶段练习)已知是关于x的方程的一个根,则该方程的另一个根为________.
2.(2022春·江苏南京·高一南京市中华中学校考期末)已知是实系数一元二次方程的两个虚数根,且满足方程.
(1)求和.
(2)写出一个以和为根的实系数一元二次方程.
3.(2022春·江西上饶·高一校联考期末)已知复数,其中i为虚数单位.
(1)若z是纯虚数,求实数m的值;
(2)若,z是关于x的实系数方程的一个复数根,求实数的值.
考点五 复数的综合运用
【例5-1】(2022春·山东临沂·高一统考期末)(多选)已知复数:满足,则( )
A.B.z的虚部为
C.z的共轭复数为D.z是方程的一个根
【例5-2】(2022春·上海闵行·高一闵行中学校考阶段练习)已知为复数,有以下四个命题,其中真命题的序号是( )
①若,则;
②若,则;
③若,则;
④若是虚数,则都是虚数.
A.①④B.②C.②③D.①②③
【一隅三反】
1.(2022春·广东广州·高一校联考期中)(多选)已知为虚数单位,则以下四个说法中正确的是( )
A.B.复数的虚部为
C.若复数为纯虚数,则D.若为复数,则为实数
2.(2022·高一单元测试)(多选)下列关于复数的命题中,正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
3.(2023·高一课时练习)已知复平面内平行四边形ABCD,A点对应的复数为,向量对应的复数为,向量对应的复数为,求:
(1)点D对应的复数;
(2)平行四边形ABCD的面积.
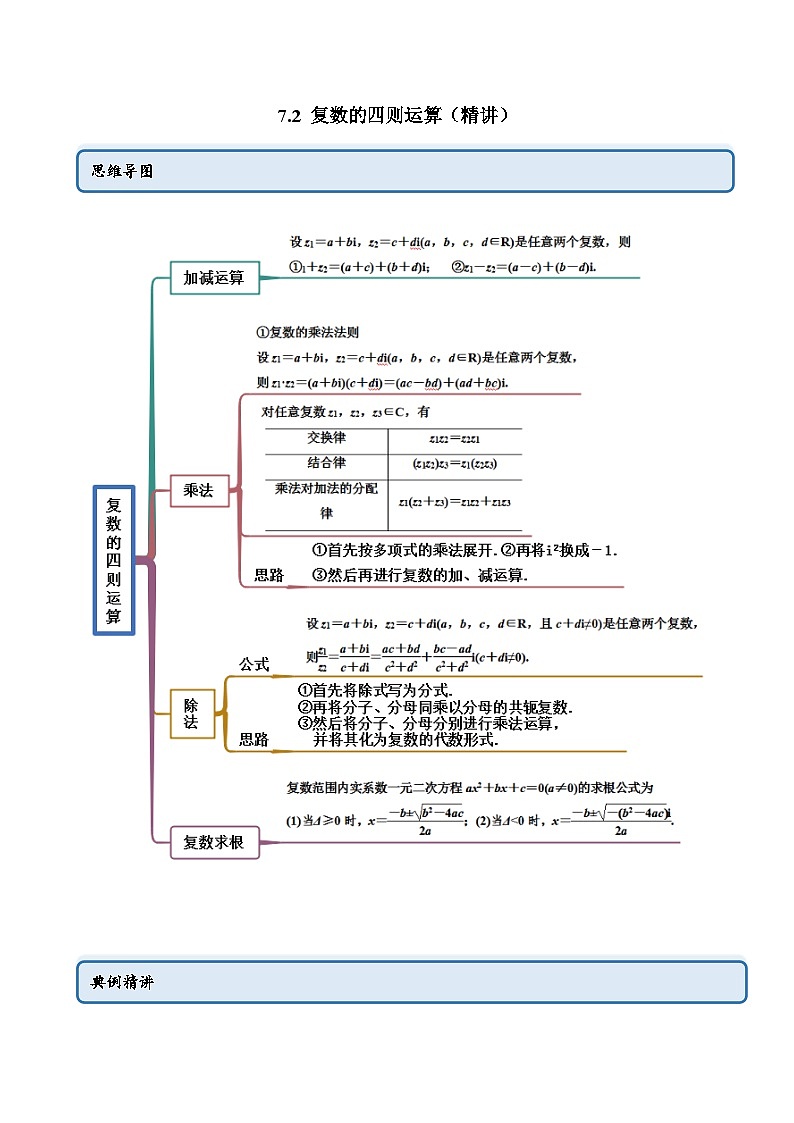
7.2 复数的四则运算(精讲)思维导图
典例精讲
考点一 复数的加减运算
【例1】(2022·高一课时练习)已知为虚数单位,计算下列各式.
(1); (2);
(3); (4).
【答案】(1);(2);(3);(4).
【解析】(1);
(2);
(3);
(4).
【一隅三反】
1.(2022广东湛江)计算:
(1); (2);
(3); (4);
(5); (6).
(7) (8)
【答案】(1)(2)(3);(4);(5)0;(6)8.(7);(8).
【解析】(1);
(2);
(3)
(4)
(5)
(6)=8
(7);
(8).
考点二 复数的乘除运算
【例2-1】(2022·高一课时练习)计算:
(1); (2);
(3); (4).
【答案】(1)4(2)(3)(4)
【解析】(1).
(2)原式.
(3).
(4)原式.
【例2-2】(2022·高一课时练习)计算:
(1); (2).(3)i+2i2+3i3+…+2 020i2 020+2 021i2 021.
【答案】(1)(2)(3)1010+1011i
【解析】(1)原式.
原式
(3)原式=(i-2-3i+4)+(5i-6-7i+8)+(9i-10-11i+12)+…+(2017i-2018-2019i+2020)+2021i=505·(2-2i)+2 021i=1010+1011i.
【一隅三反】
1.(2022·全国·高一假期作业)设,则_______.
【答案】
【解析】由题意化简,
则,故答案为:
2.(2023·高一课时练习)______.(其中i是虚数单位)
【答案】
【解析】.故答案为:
3(2023·高一课时练习)计算.
(1); (2).
(3); (4);(5).
【答案】(1)(2)(3)(4)(5)
【解析】(1)解法1:原式.
解法2:原式.
(2)原式.
(3)原式.
(4)原式.
(5),,,
原式.
考点三 共轭复数
【例3】(2022春·吉林长春·高一校考期中)已知复数,则的共轭复数为___________.
【答案】
【解析】因为,所以,所以的共轭复数为.
故答案为:
【一隅三反】
1.(2022·高一单元测试)已知为虚数单位,复数的共轭复数为( )
A.B.C.D.
【答案】C
【解析】因为,共轭复数为.故选:C.
2.(2023·全国·高一专题练习)在复平面内,复数(i为虚数单位)的共轭复数对应的点位于( ).
A.第一象限;B.第二象限;C.第三象限;D.第四象限.
【答案】D
【解析】,所以其共轭复数为,它在复平面所对应的点坐标为,位于第四象限.故选:D.
3.(2022春·辽宁沈阳·高一沈阳市第四十中学校考阶段练习)已知复数z满足,其中为虚数单位,则z的共轭复数为___________.
【答案】
【解析】由于,所以,所以.故答案为:
考点四 在复数内解方程
【例4-1】(2022·全国·高一专题练习)已知是关于x的方程的根,则实数______.
【答案】2
【解析】因为是关于x的方程的根,所以也是方程的根,
所以,得,故答案为:2
【例4-2】(2022春·上海浦东新·高一校考期末)已知关于的实系数一元二次方程有两个虚根和,且,则的值为( )
A.2B.C.D.
【答案】C
【解析】因为方程有两个虚根和,
所以,则,
又由求根公式知两虚根为,,
所以,则,解得,满足要求,
所以.故选:C.
【例4-3】(2022·高一课时练习)在复数范围内分解因式:
(1);(2).
【答案】(1)(2)
【解析】(1)由于,所以.
(2)由于,所以.
【一隅三反】
1.(2022春·福建泉州·高一校考阶段练习)已知是关于x的方程的一个根,则该方程的另一个根为________.
【答案】
【解析】是关于的方程的一个根,设该方程的另一个根为,
可得,解得.故答案为:.
2.(2022春·江苏南京·高一南京市中华中学校考期末)已知是实系数一元二次方程的两个虚数根,且满足方程.
(1)求和.
(2)写出一个以和为根的实系数一元二次方程.
【答案】(1),(2)(答案不唯一)
【解析】(1)因为是实系数一元二次方程的两个虚数根,则互为共轭复数,
设,,代入中,得,
整理得,,解得,,;
(2);,
以和为根的实系数一元二次方程可以为.
3.(2022春·江西上饶·高一校联考期末)已知复数,其中i为虚数单位.
(1)若z是纯虚数,求实数m的值;
(2)若,z是关于x的实系数方程的一个复数根,求实数的值.
【答案】(1);(2)
【解析】(1)因为复数是纯虚数,
所以解得:.
(2)当时,.
因为z是关于x的实系数方程的一个复数根,所以z的共轭复数也是实系数方程的根,所以,,解得:,,故.
考点五 复数的综合运用
【例5-1】(2022春·山东临沂·高一统考期末)(多选)已知复数:满足,则( )
A.B.z的虚部为
C.z的共轭复数为D.z是方程的一个根
【答案】AD
【解析】因为,所以,
对A:,故选项A正确;
对B:z的虚部为,故选项B错误;
对C:z的共轭复数为,故选项C错误;
对D:因为方程的根为,
所以z是方程的一个根,故选项D正确.
故选:AD.
【例5-2】(2022春·上海闵行·高一闵行中学校考阶段练习)已知为复数,有以下四个命题,其中真命题的序号是( )
①若,则;
②若,则;
③若,则;
④若是虚数,则都是虚数.
A.①④B.②C.②③D.①②③
【答案】C
【解析】为复数,
①若,因为没有大小(虚部为0,即为实数时除外),故是错误的,
②若,设,则,由,得,所以,正确,
③若,则,正确,
④若是虚数,不一定都是虚数,比如,而是虚数,故错误,
故②③正确,
故选:C.
【一隅三反】
1.(2022春·广东广州·高一校联考期中)(多选)已知为虚数单位,则以下四个说法中正确的是( )
A.B.复数的虚部为
C.若复数为纯虚数,则D.若为复数,则为实数
【答案】AD
【解析】A:,故A正确;
B:对于复数的虚部为-1,故B错误;
C:由复数z为纯虚数,设(),
则,所以,故C错误;
D:设复数(),则,
所以,故D正确.
故选:AD
2.(2022·高一单元测试)(多选)下列关于复数的命题中,正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
【答案】ABC
【解析】对于A:因为,则,则,所以,故A正确;
对于B:若,则,故B正确;
对于C:令,,,
由,所以,
所以,则,同理可得,
所以,故C正确;
对于D:令,,则,但是、,所以,故D错误;
故选:ABC
3.(2023·高一课时练习)已知复平面内平行四边形ABCD,A点对应的复数为,向量对应的复数为,向量对应的复数为,求:
(1)点D对应的复数;
(2)平行四边形ABCD的面积.
【答案】(1)5(2)7
【解析】(1)向量对应的复数为,所以向量,
对应的复数为,所以向量,
,
,
,
点对应的复数为5 .
(2),
,
,,
.
故平行四边形面积为7.
人教A版 (2019)必修 第二册7.2 复数的四则运算同步练习题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000297_t7/?tag_id=28" target="_blank">7.2 复数的四则运算同步练习题</a>,共15页。
人教A版 (2019)必修 第二册7.1 复数的概念练习: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000296_t7/?tag_id=28" target="_blank">7.1 复数的概念练习</a>,共15页。试卷主要包含了复数的实部与虚部,复数的分类,复数相等,复平面及应用,复数几何轨迹等内容,欢迎下载使用。
高中数学7.2 复数的四则运算课后练习题: 这是一份高中数学<a href="/sx/tb_c4000297_t7/?tag_id=28" target="_blank">7.2 复数的四则运算课后练习题</a>,共21页。













