






- 5.2.2同角三角函数的基本关系 课件-----2024-2025学年高一数学人教A版(2019)必修 第一册 课件 0 次下载
- 5.3 诱导公式(1)课件-----2024-2025学年高一数学人教A版(2019)必修 第一册 课件 0 次下载
- 5.3.2诱导公式 课件-----2024-2025学年高一数学人教A版(2019)必修 第一册 课件 0 次下载
- 5.4.1 正弦函数、余弦函数的图象课件-----2024-2025学年高一数学人教A版(2019)必修 第一册 课件 0 次下载
- 5.4.1正弦函数、余弦函数的图像 课件-----2024-2025学年高一数学人教A版(2019)必修 第一册 课件 0 次下载
高中数学人教A版 (2019)必修 第一册5.7 三角函数的应用图片ppt课件
展开现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象,例如地球自转引起的昼夜交替变化和公转引起的四季交替变化、月亮圆缺、潮汐变化、物体做匀速圆周运动时的位置变化、物体做简谐运动时的位移变化、交变电流变化等.
如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述.
振子运动是物理中常见的一类较为理想化的模型.通过课前查阅的弹簧振子相关资料,你能说说振子运动的原理吗?
振子的运动具有循环往复的特点,它的位移随时间的变化规律具有周期性,并且振子在某一中心位置两侧做往复运动,这个中心位置就是平衡位置.
全振动是从任一时刻起,物体的运动状态(位置、速度、加速度)再次恢复到与该时刻完全相同所经历的过程.
你能结合振子运动相关知识完成下面的问题1吗?
问题1 某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t (单位:s)与位移 y (单位: mm )之间的对应数据如表所示,试根据这些数据确定这个振子的位移关于时间的函数解析式.
表示函数有哪些方法?如何让表格中数据反映出的位移随时间变化的规律更直观?
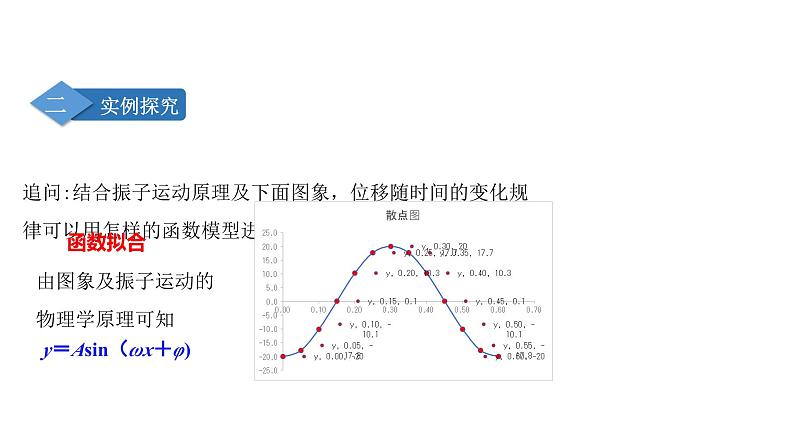
追问:结合振子运动原理及下面图象,位移随时间的变化规律可以用怎样的函数模型进行刻画?
y=Asin(ωx+φ)
由图象及振子运动的物理学原理可知
分析:振子振动时位移的最大值为20mm,因此A=20;
所以振子的位移关于时间的函数解析式为
所以当时间t=5s时振子的位移约为10mm.
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等.这些都是物体在某一中心位置附近循环往复的运动.
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.
可以证明,在适当的直角坐标系下,简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞) ,其中A>0,ω>0,来表示.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
A是简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
可以看到我们在物理学中把三角函数中的三个参数都赋予了物理意义.
某简谐振动的图象如图所示,试根据图象回答下列问题:(1)这个简谐振动的振幅、周期与频率各是多少?(2)写出这个简谐振动的函数解析式.
解:(1)根据图象所示,振幅A=3(cm),
则这个简谐振动的函数解析式为
问题2 如图(1)是某次实验测得的交变电流i(单位:A)随时间(单位:s)变化的图象.将测得的图象放大,得到图(2).(1)求电流i随时间t变化的函数解析式;
观察函数图象你发现电流随时间变化有什么特点?可以用什么函数刻画?
此时,i=5sin(100πt+φ),再由初始状态(t=0)的电流为4.33A,
(1)先求振幅A:观察图象最高点和最低点来确定;
通过前面的两个三角函数模型问题学习,你能总结利用函数图象求解析式步骤吗?
(2)再由周期T求ω:通过图象分析周期T;
(3)最后求初相φ:通过代入图象上的特殊点求出φ的值.
1.函数y=Asin(ωx+φ),x∈[0,+∞) ,其中A>0,ω>0, 中参数的物理意义
x=0 时的相位φ称为初相
高中数学人教A版 (2019)必修 第一册4.3 对数课文配套ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000275_t3/?tag_id=26" target="_blank">4.3 对数课文配套ppt课件</a>,共18页。PPT课件主要包含了问题提出,指数式与对数式的关系,零与负数没有对数,小组探究,N的常用对数,N的自然对数,简记作,两个重要对数,常用对数,自然对数等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.2.2 指数函数的图象和性质教学ppt课件: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4053117_t3/?tag_id=26" target="_blank">4.2.2 指数函数的图象和性质教学ppt课件</a>,共17页。PPT课件主要包含了复习回顾导入新课,数学必修1,合作探究构建新知,图象都在x轴上方,都是非奇非偶函数,0a1,新知应用巩固内化,归纳总结反思提升,课后作业巩固延伸等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.1 指数课文课件ppt: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000273_t3/?tag_id=26" target="_blank">4.1 指数课文课件ppt</a>,共27页。PPT课件主要包含了方根和根式,n次方根的定义,-2叫4的平方根,叫8的立方根,-23-8,-2叫-8的立方根,叫16的4次方根,叫a的n次方根,叫4的平方根,-2叫16的4次方根等内容,欢迎下载使用。













