初中青岛版2.4 线段的垂直平分线完整版课件ppt

这是一份初中青岛版2.4 线段的垂直平分线完整版课件ppt，共60页。PPT课件主要包含了第二章图形的轴对称，青岛版八年级数学上册，第二课时，学习目标，实验与探究，2作法，归纳提升，作线段的垂直平分线，分类讨论的数学思想，转化的数学思想等内容，欢迎下载使用。

2.4 线段的垂直平分线
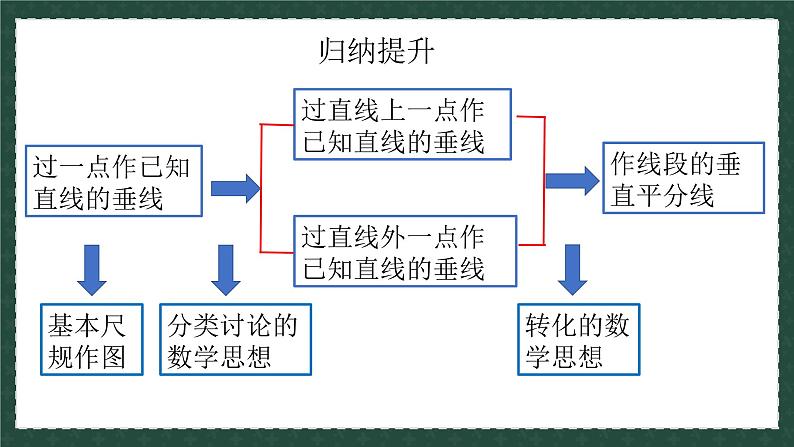
能用尺规完成基本作图：过一点作已知直线的垂线
在尺规作图中，了解作图的道理，保留作图的痕迹
利用过一点作已知直线的垂线解决最短路径问题.
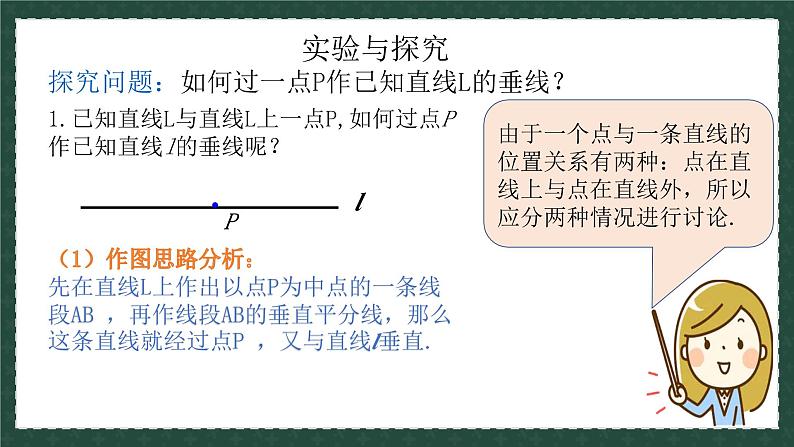
探究问题：如何过一点P作已知直线L的垂线？
1.已知直线L与直线L上一点P,如何过点P作已知直线l的垂线呢？
（1）作图思路分析：先在直线L上作出以点P为中点的一条线段AB ，再作线段AB的垂直平分线，那么这条直线就经过点P ，又与直线l垂直.
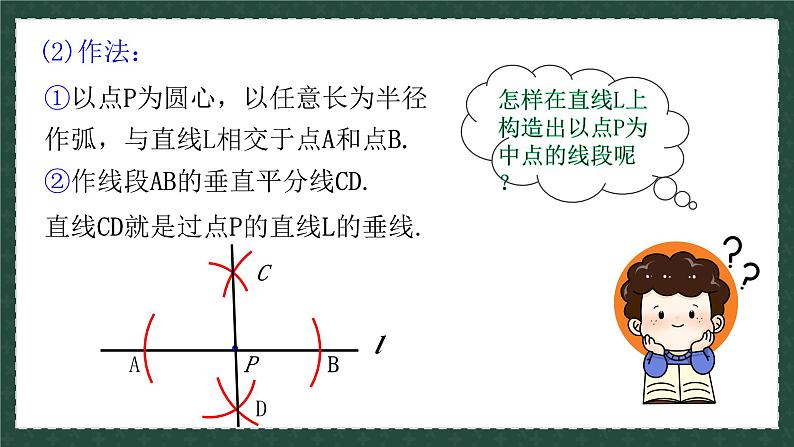
①以点P为圆心，以任意长为半径作弧，与直线L相交于点A和点B.
②作线段AB的垂直平分线CD.
直线CD就是过点P的直线L的垂线.
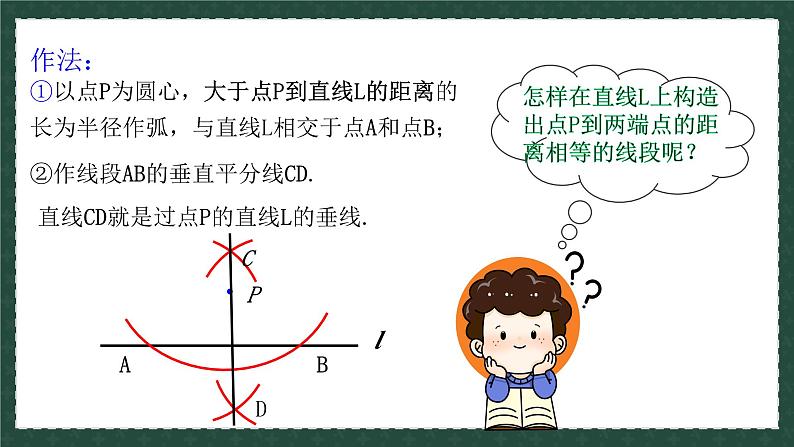
2.已知直线L与直线L外一点P,如何过点P作已知直线l的垂线呢？
（1）作图思路：先在直线L上作出一条线段AB ，并且使点P到线段AB两端的距离相等，再作线段AB的垂直平分线，那么这条直线经过点P ，又与直线L垂直.
①以点P为圆心，大于点P到直线L的距离的长为半径作弧，与直线L相交于点A和点B；②作线段AB的垂直平分线CD.
过一点作已知直线的垂线
过直线外一点作已知直线的垂线
过直线上一点作已知直线的垂线
1.已知△ABC，求作AC边上的高.
2.如图，已知线段a，锐角α，求作Rt△ABC，使∠C=90°，BC=a,∠B=α
例1 海伦是古希腊的一位数学家，测量学家.相传，有一天一位将军专程拜访海伦，求教一个令他百思不得其解的问题：“我每天策马往返于两个边防站A与B之间，途中都要到小河L边让马饮水.怎样走路程最近呢？”你能帮将军解答这个问题吗？说出你的作法，在图中作出最近的路线.
将本题抽象为数学语言：已知点A ，B两点在直线L的同侧，在直线l上求作一点P，使AP+BP的值最小.
(1)你能将这个实际问题转化为数学问题吗？
（2）作点B关于直线L的对称点B'，连接PB'，
此时PB与PB'有什么关系?
(3)现在求AP+BP的最小值问题就转化为什么问题了？
求AP+B'P的最小值问题
（4）AP+B'P的长度可以看作哪两点之间的一条路径长？
（5）从A点出发，经过直线L上一点，最终到达点B'的路径有无数条，其中哪一条最短？
作法：(1)过点B作直线L的垂线BC，垂足为C；(2)在BC上截取点B′，使B，B′分别在L的两侧，且CB′= CB；(3)连接AB′，与直线L交于点P；点P就是所求作的直线L上使AP+BP的值最小的点
当两个点在一条直线的同侧时，我们就可以按照这个图形在直线上作出到这两点距离之和最小的点了.
1．如图，在△ABC中，AC=2，，EF垂直平分BC，点P是直线EF上的任意一点，求AP+PC的最小值．
连接PC∵EF是BC的垂直平分线∴PB=PC∴AP+PB=AP+PC∴当点A,P,C在一条直线上时，AP+PC有最小值，且最小值=AC=3．
2.已知如图，在∠AOB内有一定点P，点M为边OA上一动点，点N为边OB上一动点，当△PMN的周长最小时，你能画出点M与点N的位置吗?
3.如图，A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点.