
还剩7页未读,
继续阅读
2021学年第2章 图形的轴对称2.4 线段的垂直平分线当堂检测题
展开
这是一份2021学年第2章 图形的轴对称2.4 线段的垂直平分线当堂检测题,共10页。试卷主要包含了下列说法错误的是等内容,欢迎下载使用。
1.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是( )
A.10°B.15°C.20°D.25°
2.如图,在Rt△ABC中,∠C=90°,DE是斜边AB的垂直平分线,与BC相交于点D连接AD,若AC=5,△ACD的周长为17,则斜边AB的长为( )
A.11B.12C.13D.14
3.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠PAQ=40°,则∠BAC的度数是( )
A.110°B.100°C.120°D.70°
4.下列说法错误的是( )
A.三角形的三条高的交点一定在三角形内部
B.三角形的三条中线的交点一定在三角形内部
C.三角形的三条角平分线的交点一定在三角形内部
D.三角形的三条边的垂直平分线的交点可能在三角形内部,也可能在三角形外部
5.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC﹣AC=2,则BC的长为( )
A.4B.6C.8D.10
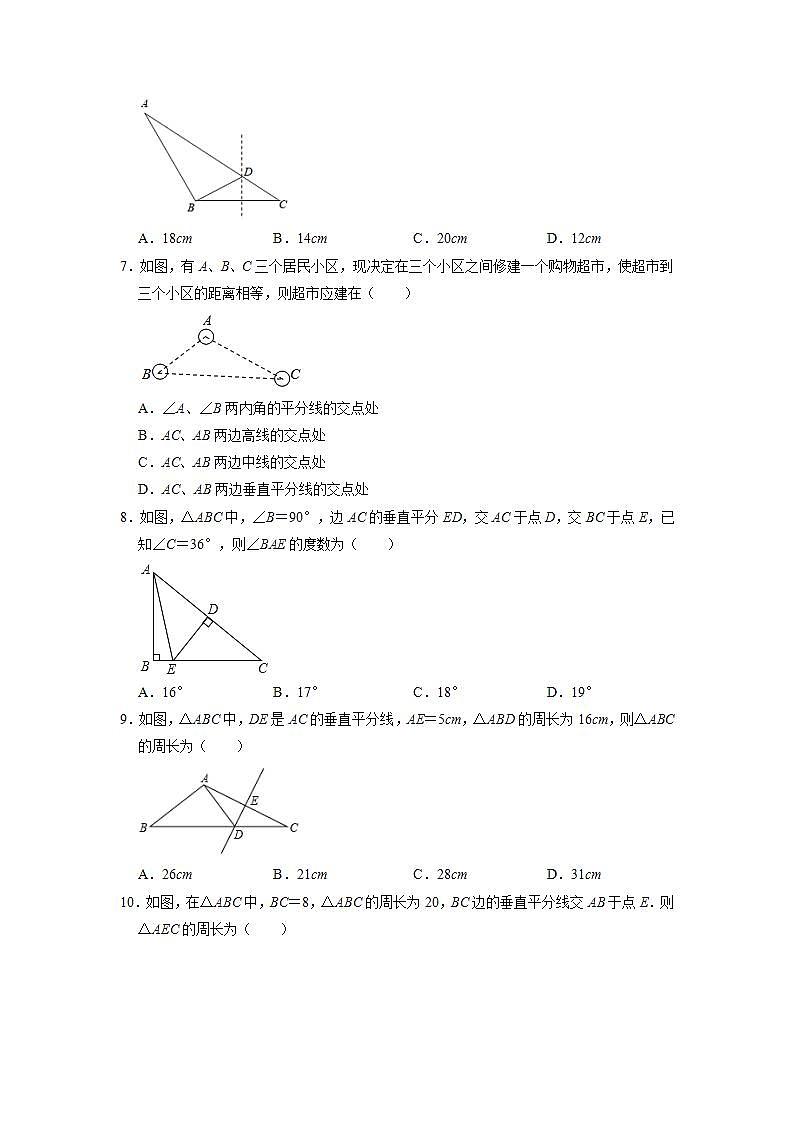
6.如图,△ABC的边长AB=8cm,AC=10cm,BC=4cm,作BC的垂直平分线交AC于D,则△ABD的周长为( )
A.18cmB.14cmC.20cmD.12cm
7.如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.∠A、∠B两内角的平分线的交点处
B.AC、AB两边高线的交点处
C.AC、AB两边中线的交点处
D.AC、AB两边垂直平分线的交点处
8.如图,△ABC中,∠B=90°,边AC的垂直平分ED,交AC于点D,交BC于点E,已知∠C=36°,则∠BAE的度数为( )
A.16°B.17°C.18°D.19°
9.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cmB.21cmC.28cmD.31cm
10.如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB于点E.则△AEC的周长为( )
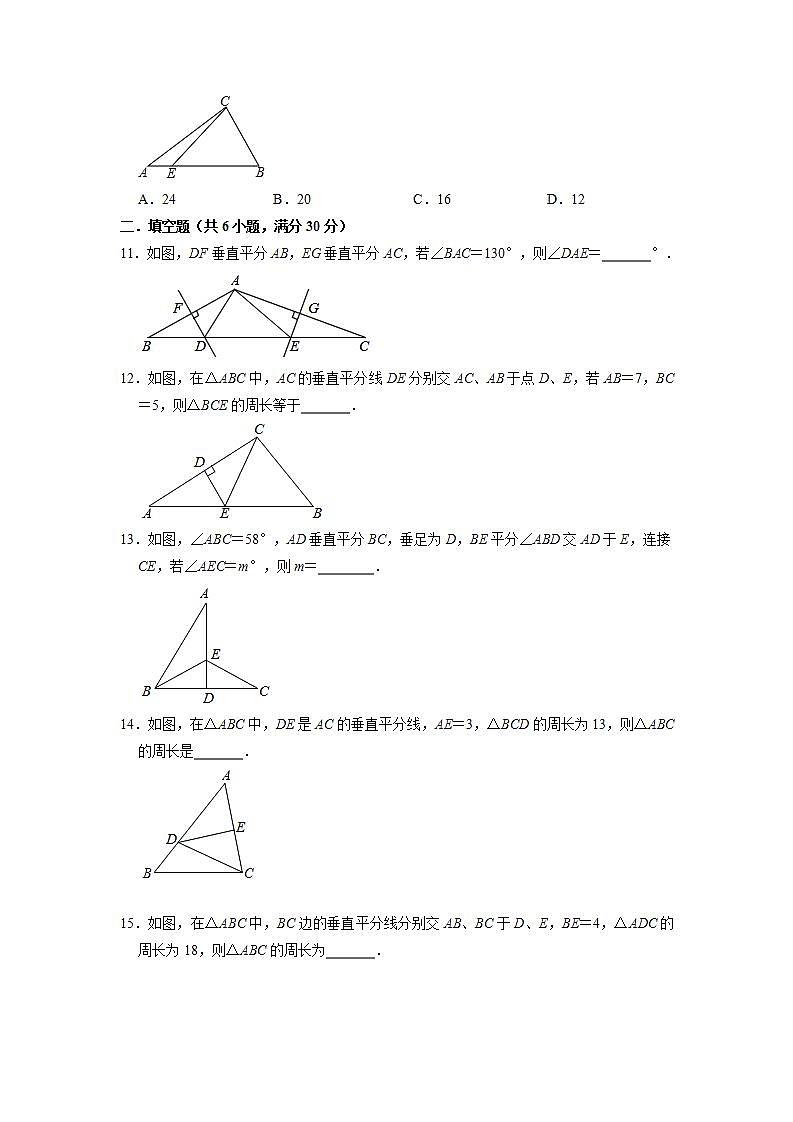
A.24B.20C.16D.12
二.填空题(共6小题,满分30分)
11.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=130°,则∠DAE= °.
12.如图,在△ABC中,AC的垂直平分线DE分别交AC、AB于点D、E,若AB=7,BC=5,则△BCE的周长等于 .
13.如图,∠ABC=58°,AD垂直平分BC,垂足为D,BE平分∠ABD交AD于E,连接CE,若∠AEC=m°,则m= .
14.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△BCD的周长为13,则△ABC的周长是 .
15.如图,在△ABC中,BC边的垂直平分线分别交AB、BC于D、E,BE=4,△ADC的周长为18,则△ABC的周长为 .
16.如图,线段AB,BC的垂直平分线l1,l2交于点O.若∠B=35°,则∠AOC= °.
三.解答题(共5小题,满分40分)
17.如图,△ABC中,∠C=90°,DE垂直平分AB,若∠B=25°,求∠CAE的度数.
18.如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18cm,求DE的长.
19.如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=∠2,求∠B的度数.
20.如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,BE平分∠CBA,求∠A的度数.
21.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵∠B=90°,∠A=40°,
∴∠ACB=90°﹣40°=50°,
∵MN是AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=40°,
∴∠BCD=∠ACB﹣∠ACD=10°,
故选:A.
2.解:∵DE是AB的垂直平分线,
∴DA=DB,
∵△ACD的周长为17,
∴AC+CD+AD=17,
∴AC+CD+DB=AC+BC=17,
∵AC=5,
∴BC=17﹣5=12,
由勾股定理得,AB==13,
故选:C.
3.解:∵PM、QN分别是线段AB、AC的垂直平分线,
∴PA=PB,QA=QC,
∴∠PAB=∠B,∠QAC=∠C,
∴∠PAB+∠QAC=∠B+∠C,
∵∠PAB+∠B+∠PAQ+∠QAC+∠C=180°,
∴∠PAB+∠QAC=70°,
∴∠BAC=∠PAB+∠QAC+∠PAQ=110°,
故选:A.
4.解:A、三角形的三条高的交点在三角形内部、外部或顶点上,本选项说法错误,符合题意;
B、三角形的三条中线的交点一定在三角形内部,本选项说法正确,不符合题意;
C、三角形的三条角平分线的交点一定在三角形内部,本选项说法正确,不符合题意;
D、三角形的三条边的垂直平分线的交点可能在三角形内部,也可能在三角形外部,本选项说法正确,不符合题意;
故选:A.
5.解:∵DE是线段AB的垂直平分线,
∴DA=DB,
∵△ADC的周长为10,
∴AC+DC+AD=10,
∴AC+CD+BD=AC+BC=10,
∵BC﹣AC=2,
∴BC=6,
故选:B.
6.解:∵BC的垂直平分线交AC于D,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=8+10=18(cm),
故选:A.
7.解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在AC、AB两边垂直平分线的交点处,
故选:D.
8.解:在Rt△ABC中,∠B=90°,∠C=36°,
∴∠BAC=90°﹣36°=54°,
∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=36°,
∴∠BAE=∠BAC﹣∠CAE=18°,
故选:C.
9.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长为16,
∴AB+BD+AD=AB+BD+DC=AB+BC=16,
∴△ABC的周长=AB+BC+AC=16+10=26(cm),
故选:A.
10.解:∵△ABC的周长为20,
∴AB+AC+BC=20,
∵BC=8,
∴AB+AC=12,
∵BC边的垂直平分线交AB于点E,
∴EB=EC,
∴△AEC的周长=AE+EC+AC=AE+EB+AC=AB+AC=12,
故选:D.
二.填空题(共6小题,满分30分)
11.解:∵∠BAC=130°,
∴∠B+∠C=180°﹣130°=50°,
∵DF垂直平分AB,EG垂直平分AC,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=50°,
∴∠DAE=∠BAC﹣(∠B+∠C)=80°,
故答案为:80.
12.解:∵DE是AC的垂直平分线,
∴EA=EC,
∴△BCE的周长=BC+BE+EC=BC+BE+EA=BC+AB=12,
故答案为:12.
13.解:∵BE平分∠ABD,∠ABC=58°,
∴∠EBC=∠ABC=29°,
∵AD垂直平分BC,
∴EB=EC,∠ADC=90°,
∴∠C=∠EBC=29°,
∴∠AEC=∠ADC+∠C=119°,即m=119,
故答案为:119.
14.解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△BCD的周长为13,
∴BC+BD+CD=13,
∴BC+BD+DA=BC+AB=13,
∴△ABC的周长=BC+AB+AC=13+6=19,
故答案为:19.
15.解:∵DE是线段BC的垂直平分线,BE=4,
∴DB=DC,BC=2BE=8,
∵△ADC的周长为18,
∴AC+AD+DC=18,
∴AC+AD+DB=AC+AB=18,
∴△ABC的周长=AC+AB+BC=26,
故答案为:26.
16.解:连接BO并延长,点D在BO的延长线上
∵线段AB,BC的垂直平分线l1,l2交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠ABO,∠COD=2∠CBO,
∴∠AOC=∠AOD+∠COD=2(∠ABO+∠CBO)=70°,
故答案为:70.
三.解答题(共5小题,满分40分)
17.解:∵DE垂直平分AB,
∴EA=EB,
∵∠B=25°,
∴∠EAB=∠B=25°,
∵∠C=90°,
∴∠CAB=65°,
∴∠CAE=65°﹣25°=40°.
18.解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
19.解:DE垂直平分AB,
∴AD=BD,
∴∠2=∠B,
∵∠1=∠2,
∴∠1=∠B,
∴∠BAC=∠1+∠2=∠B,
∵在△ABC中,∠C=90°,
∴∠BAC+∠B=∠B=90°,
∴∠B=36°.
20.解:∵ED是AB边的垂直平分线,
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,BE平分∠CBA,
∴∠A+∠ABC=90°,即3x=90°,
解得x=30°,
∴∠A=30°.
21.解:(1)∵边AB、AC的垂直平分线分别交BC于D、E,
∴DA=DB,EA=EC,
∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠DAB+∠EAC=60°,
∴∠BAC=120°.
1.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是( )
A.10°B.15°C.20°D.25°
2.如图,在Rt△ABC中,∠C=90°,DE是斜边AB的垂直平分线,与BC相交于点D连接AD,若AC=5,△ACD的周长为17,则斜边AB的长为( )
A.11B.12C.13D.14
3.如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠PAQ=40°,则∠BAC的度数是( )
A.110°B.100°C.120°D.70°
4.下列说法错误的是( )
A.三角形的三条高的交点一定在三角形内部
B.三角形的三条中线的交点一定在三角形内部
C.三角形的三条角平分线的交点一定在三角形内部
D.三角形的三条边的垂直平分线的交点可能在三角形内部,也可能在三角形外部
5.如图,在△ABC中,AB的垂直平分线交AB于点E,交BC于点D,△ADC的周长为10,且BC﹣AC=2,则BC的长为( )
A.4B.6C.8D.10
6.如图,△ABC的边长AB=8cm,AC=10cm,BC=4cm,作BC的垂直平分线交AC于D,则△ABD的周长为( )
A.18cmB.14cmC.20cmD.12cm
7.如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.∠A、∠B两内角的平分线的交点处
B.AC、AB两边高线的交点处
C.AC、AB两边中线的交点处
D.AC、AB两边垂直平分线的交点处
8.如图,△ABC中,∠B=90°,边AC的垂直平分ED,交AC于点D,交BC于点E,已知∠C=36°,则∠BAE的度数为( )
A.16°B.17°C.18°D.19°
9.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cmB.21cmC.28cmD.31cm
10.如图,在△ABC中,BC=8,△ABC的周长为20,BC边的垂直平分线交AB于点E.则△AEC的周长为( )
A.24B.20C.16D.12
二.填空题(共6小题,满分30分)
11.如图,DF垂直平分AB,EG垂直平分AC,若∠BAC=130°,则∠DAE= °.
12.如图,在△ABC中,AC的垂直平分线DE分别交AC、AB于点D、E,若AB=7,BC=5,则△BCE的周长等于 .
13.如图,∠ABC=58°,AD垂直平分BC,垂足为D,BE平分∠ABD交AD于E,连接CE,若∠AEC=m°,则m= .
14.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△BCD的周长为13,则△ABC的周长是 .
15.如图,在△ABC中,BC边的垂直平分线分别交AB、BC于D、E,BE=4,△ADC的周长为18,则△ABC的周长为 .
16.如图,线段AB,BC的垂直平分线l1,l2交于点O.若∠B=35°,则∠AOC= °.
三.解答题(共5小题,满分40分)
17.如图,△ABC中,∠C=90°,DE垂直平分AB,若∠B=25°,求∠CAE的度数.
18.如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18cm,求DE的长.
19.如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=∠2,求∠B的度数.
20.如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,BE平分∠CBA,求∠A的度数.
21.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵∠B=90°,∠A=40°,
∴∠ACB=90°﹣40°=50°,
∵MN是AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=40°,
∴∠BCD=∠ACB﹣∠ACD=10°,
故选:A.
2.解:∵DE是AB的垂直平分线,
∴DA=DB,
∵△ACD的周长为17,
∴AC+CD+AD=17,
∴AC+CD+DB=AC+BC=17,
∵AC=5,
∴BC=17﹣5=12,
由勾股定理得,AB==13,
故选:C.
3.解:∵PM、QN分别是线段AB、AC的垂直平分线,
∴PA=PB,QA=QC,
∴∠PAB=∠B,∠QAC=∠C,
∴∠PAB+∠QAC=∠B+∠C,
∵∠PAB+∠B+∠PAQ+∠QAC+∠C=180°,
∴∠PAB+∠QAC=70°,
∴∠BAC=∠PAB+∠QAC+∠PAQ=110°,
故选:A.
4.解:A、三角形的三条高的交点在三角形内部、外部或顶点上,本选项说法错误,符合题意;
B、三角形的三条中线的交点一定在三角形内部,本选项说法正确,不符合题意;
C、三角形的三条角平分线的交点一定在三角形内部,本选项说法正确,不符合题意;
D、三角形的三条边的垂直平分线的交点可能在三角形内部,也可能在三角形外部,本选项说法正确,不符合题意;
故选:A.
5.解:∵DE是线段AB的垂直平分线,
∴DA=DB,
∵△ADC的周长为10,
∴AC+DC+AD=10,
∴AC+CD+BD=AC+BC=10,
∵BC﹣AC=2,
∴BC=6,
故选:B.
6.解:∵BC的垂直平分线交AC于D,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=8+10=18(cm),
故选:A.
7.解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在AC、AB两边垂直平分线的交点处,
故选:D.
8.解:在Rt△ABC中,∠B=90°,∠C=36°,
∴∠BAC=90°﹣36°=54°,
∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=36°,
∴∠BAE=∠BAC﹣∠CAE=18°,
故选:C.
9.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长为16,
∴AB+BD+AD=AB+BD+DC=AB+BC=16,
∴△ABC的周长=AB+BC+AC=16+10=26(cm),
故选:A.
10.解:∵△ABC的周长为20,
∴AB+AC+BC=20,
∵BC=8,
∴AB+AC=12,
∵BC边的垂直平分线交AB于点E,
∴EB=EC,
∴△AEC的周长=AE+EC+AC=AE+EB+AC=AB+AC=12,
故选:D.
二.填空题(共6小题,满分30分)
11.解:∵∠BAC=130°,
∴∠B+∠C=180°﹣130°=50°,
∵DF垂直平分AB,EG垂直平分AC,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=50°,
∴∠DAE=∠BAC﹣(∠B+∠C)=80°,
故答案为:80.
12.解:∵DE是AC的垂直平分线,
∴EA=EC,
∴△BCE的周长=BC+BE+EC=BC+BE+EA=BC+AB=12,
故答案为:12.
13.解:∵BE平分∠ABD,∠ABC=58°,
∴∠EBC=∠ABC=29°,
∵AD垂直平分BC,
∴EB=EC,∠ADC=90°,
∴∠C=∠EBC=29°,
∴∠AEC=∠ADC+∠C=119°,即m=119,
故答案为:119.
14.解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△BCD的周长为13,
∴BC+BD+CD=13,
∴BC+BD+DA=BC+AB=13,
∴△ABC的周长=BC+AB+AC=13+6=19,
故答案为:19.
15.解:∵DE是线段BC的垂直平分线,BE=4,
∴DB=DC,BC=2BE=8,
∵△ADC的周长为18,
∴AC+AD+DC=18,
∴AC+AD+DB=AC+AB=18,
∴△ABC的周长=AC+AB+BC=26,
故答案为:26.
16.解:连接BO并延长,点D在BO的延长线上
∵线段AB,BC的垂直平分线l1,l2交于点O,
∴OA=OB,OC=OB,
∴∠OAB=∠OBA,∠OCB=∠OBC,
∴∠AOD=2∠ABO,∠COD=2∠CBO,
∴∠AOC=∠AOD+∠COD=2(∠ABO+∠CBO)=70°,
故答案为:70.
三.解答题(共5小题,满分40分)
17.解:∵DE垂直平分AB,
∴EA=EB,
∵∠B=25°,
∴∠EAB=∠B=25°,
∵∠C=90°,
∴∠CAB=65°,
∴∠CAE=65°﹣25°=40°.
18.解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
19.解:DE垂直平分AB,
∴AD=BD,
∴∠2=∠B,
∵∠1=∠2,
∴∠1=∠B,
∴∠BAC=∠1+∠2=∠B,
∵在△ABC中,∠C=90°,
∴∠BAC+∠B=∠B=90°,
∴∠B=36°.
20.解:∵ED是AB边的垂直平分线,
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,BE平分∠CBA,
∴∠A+∠ABC=90°,即3x=90°,
解得x=30°,
∴∠A=30°.
21.解:(1)∵边AB、AC的垂直平分线分别交BC于D、E,
∴DA=DB,EA=EC,
∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠B+∠C=∠DAB+∠EAC=60°,
∴∠BAC=120°.













