




初中数学青岛版八年级上册2.1 图形的轴对称试讲课ppt课件
展开它 们 有 什 么 共 同 特 征 ?
直线两旁的部分完全一样
2.1 图形的轴对称
了解轴对称以及两个图形关于某条直线成轴对称的概念.
会判断两个图形是否关于某条直线成轴对称.
会利用成轴对称的两个图形是全等形进行相关计算.
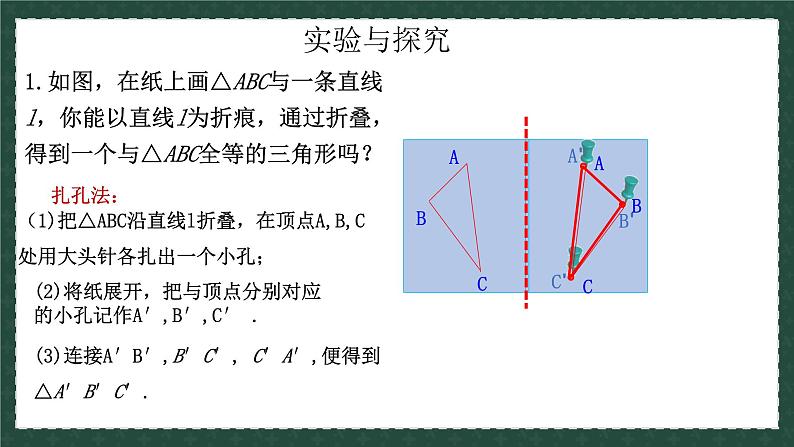
1.如图,在纸上画△ABC与一条直线l,你能以直线l为折痕,通过折叠,得到一个与△ABC全等的三角形吗?
(1)把△ABC沿直线l折叠,在顶点A,B,C处用大头针各扎出一个小孔;
(2)将纸展开,把与顶点分别对应的小孔记作A′,B′,C′ .
(3)连接A′B′,B′C′, C′A′,便得到△A′B′C′.
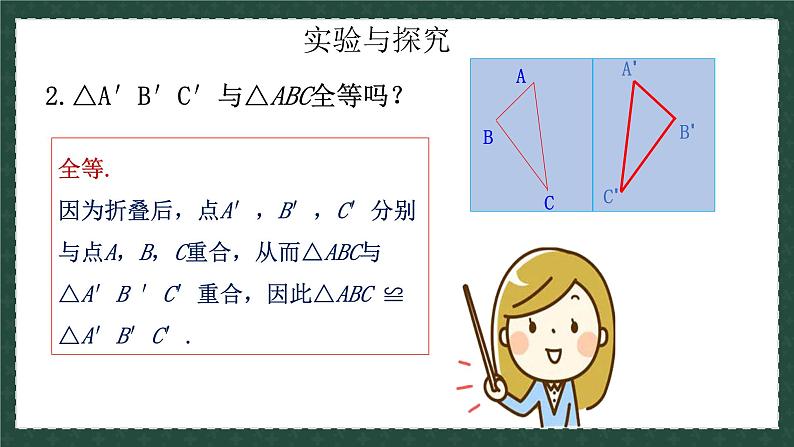
2.△A′B′C′与△ABC全等吗?
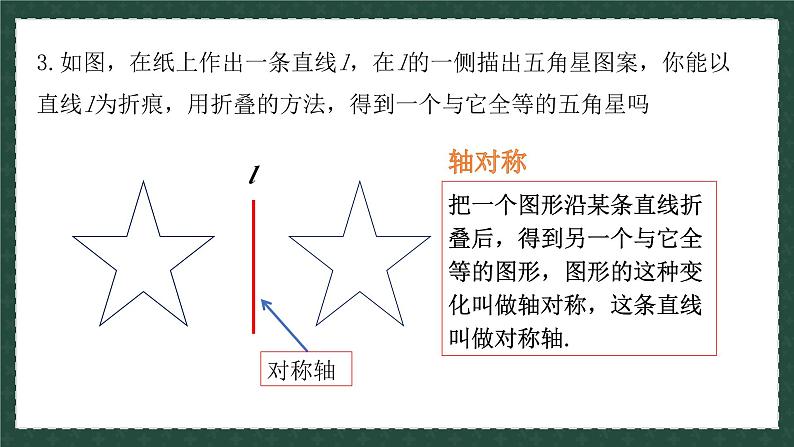
3.如图,在纸上作出一条直线l,在l的一侧描出五角星图案,你能以直线l为折痕,用折叠的方法,得到一个与它全等的五角星吗
把一个图形沿某条直线折叠后,得到另一个与它全等的图形,图形的这种变化叫做轴对称,这条直线叫做对称轴.
(1)对称轴是一条直线,而不是射线或线段;(2)轴对称是图形的一种变化,而不是图形.(3)轴对称实质:轴对称是一种全等变换.一个图形以不同的直线为对称轴,经轴对称得到的图形只是位置不同,但都是全等形.
4.观察图①中的两个图案,把其中一个图案以直线n为对称轴,经过轴对称后,能与另一个图案重合吗?图②、图③呢?
一个图形以某条直线为对称轴,经过轴对称后,能够与另一个图形重合,就说这两个图形关于这条直线成轴对称,重合的点叫做对应点.特别地,如果两个点关于一条直线成轴对称,其中一个点叫做另一个点关于这条直线的对称点.
两个三角形关于直线l成轴对称
点A,B,C的对应点分别是点A′, B′,C′
思考:(1)成轴对称与轴对称有什么区别吗?
(2)成轴对称的两个图形一定全等吗?
(3)两个全等形一定成轴对称吗?
成轴对称是两个全等图形存在的某种特殊的位置关系;而轴对称是图形变换的一种方式.
例1: 如图,△ABC与△DEF关于直线l成轴对称.如果DE=3cm, ∠A=75°,∠E=43°,求AB的长与∠B,∠C,∠D,∠F的度数.
解:∵△ABC与△DEF关于直线l成轴对称 ∴△ABC ≌ △DEF
∴AB=DE=3,∠B=∠E= 43°,∠D=∠A=75°
∴∠C=180°-∠A-∠B=62°
对应角相等,对应边相等
1.下列选项中,每组中的两个图形成轴对称的是( )
2.下列说法错误的是( ) A.两个成轴对称的图形一定不会存在于对称轴的同侧。 B.关于某直线对称的两个图形形状、大小相同。 C.成轴对称的两个图形只有一条对称轴。 D.全等三角形一定成轴对称
3.如图,△ABC与△DEF关于直线MN成轴对称.(1) 若AB=7cm,则DE=_________;(2) 若∠A=70°,∠B=50°,则∠F=______;(3) 若S△DEF =68cm2,则S△ABC=___________.
【思路点拨】由折叠可得成轴对称的图形,然后根据成轴对称的图形的性质可求∠ABE的度数
数学八年级上册1.3 尺规作图一等奖课件ppt: 这是一份数学八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图一等奖课件ppt</a>,共16页。PPT课件主要包含了第一章全等三角形,青岛版八年级数学上册,第三课时,学习目标,实验与探究,思路分析,你做对了吗,转化的数学思想,归纳总结,先画草图等内容,欢迎下载使用。
初中数学青岛版八年级上册1.3 尺规作图精品ppt课件: 这是一份初中数学青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图精品ppt课件</a>,共16页。PPT课件主要包含了第一章全等三角形,青岛版八年级数学上册,第二课时,学习目标,实验与探究,图1-28,确定三个顶点的位置,成果展示,图1-29,①作∠B∠α等内容,欢迎下载使用。
青岛版八年级上册1.3 尺规作图完美版课件ppt: 这是一份青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图完美版课件ppt</a>,共16页。PPT课件主要包含了3cm,第一章全等三角形,青岛版八年级数学上册,第一课时,学习目标,交流与发现,无刻度的直尺,作过任意一点的直线,连接两个点作一条线段,经过两点作一条直线等内容,欢迎下载使用。













