








初中数学人教版(2024)七年级上册2.1 有理数的加法与减法习题ppt课件
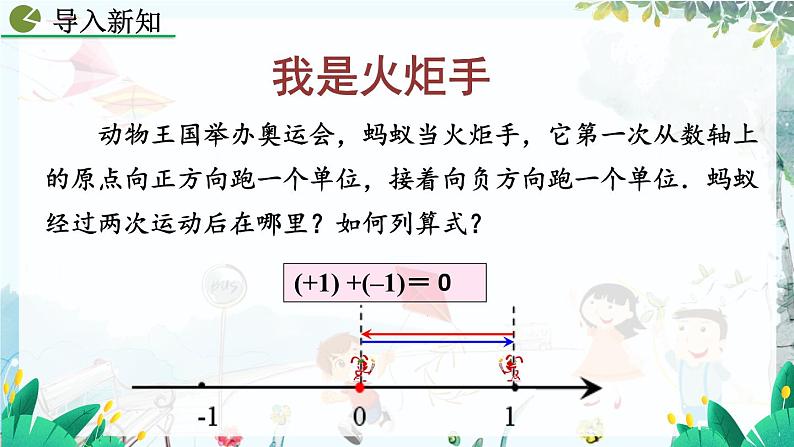
展开(+1) +(–1)=
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.
一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.
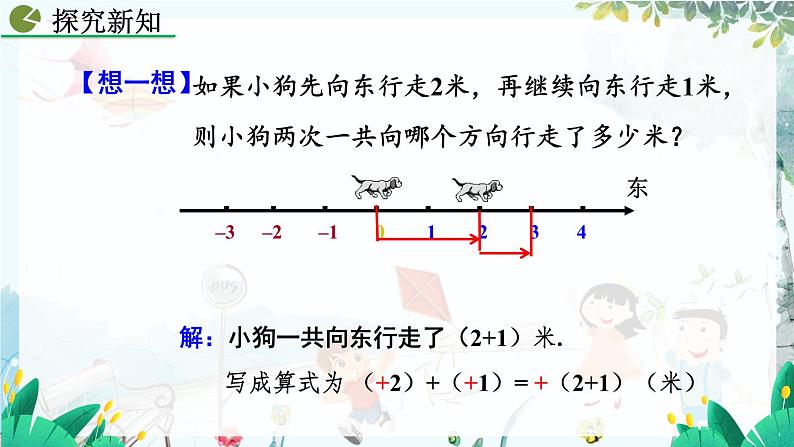
如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?
解:小狗一共向东行走了(2+1)米.
写成算式为 (+2)+(+1)= +(2+1)(米)
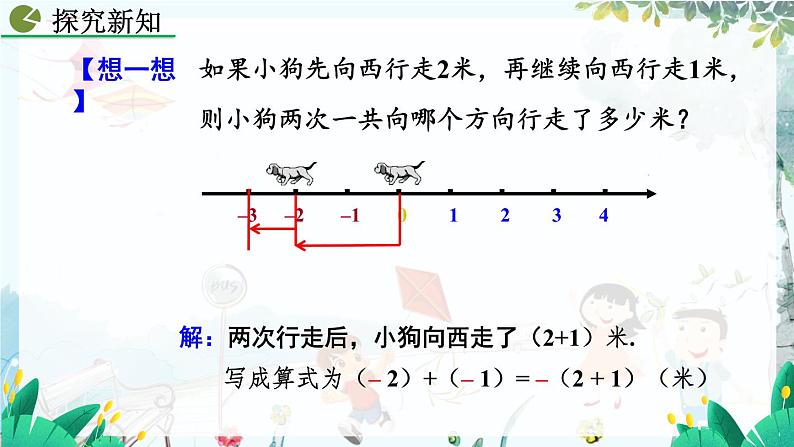
如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?
解:两次行走后,小狗向西走了(2+1)米.
写成算式为(– 2)+(– 1)= –(2 + 1)(米)
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
解:小狗两次一共向西走了(3–2)米.
用算式表示为 –3+(+2)= –(3–2)(米)
如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?
解:小狗两次一共向东走了(3–2)米.
用算式表示为 –2 +(+3)= +(3–2)(米)
如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
写成算式为(–2)+(+2)= 0(米)
解:小狗一共行走了0米.
–2 + (+3) = +(3–2) –3 + (+2)= –(3–2) –2 + (+2)= (2–2)
你从上面三个式子中发现了什么?
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
解:小狗向西行走了3米.
写成算式为(–3)+0= –3(米)
一个数同0相加,仍得这个数.
1.同号两数相加,结果取相同符号,并把绝对值相加.2.绝对值不相等的异号两数相加,结果取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.3.一个数同0相加,仍得这个数.
例1 计算: (1)(–4)+(–8); (2)(–5)+13; (3) 0 +(–7); (4)(–4.7)+4.7.
解: (1)(–4)+(–8)= –(4+8)= –12
利用有理数的加法法则进行运算
(2)(–5)+13=+(13–5)= 8
(3) 0 +(–7)= –7
(4)(–4.7)+4.7=0
通过有理数加法法则的学习,同学们,你们认为如何进行有理数加法运算呢?
方法总结: 1.先判断类型(同号、异号等); 2.再确定和的符号; 3.最后进行绝对值的加减运算.
计算: (1) ; (2) ; (3) ; (4) .
例2 已知│a│= 8,│b│= 2; (1)当a、b同号时,求a+b的值; (2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值.
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
(1)因为a、b同号,所以a= 8,b= 2或a= –8,b= –2.
所以a+b= 8+2=10或a+b= – 8+(–2)= –10.
(2)因为a、b异号,所以a= 8,b=– 2或a= –8,b= 2.
所以a+b= 8+(–2)= 6或a+b= – 8+2= – 6.
若|x–3|与|y+2|互为相反数,求x+y的值.
解:由题意得|x–3|+|y+2|=0,又|x–3|≥0,|y+2|≥0, 所以x–3= 0,y+2=0,所以x=3 ,y= –2.
所以x+y=3–2=1.
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0, 蓝队胜红队1:0,计算各队的净胜球数.
解:每个队的进球总数记为正数,失球总数记为负数,这两数 的和为这队的净胜球数. 三场比赛中,红队共进4球,失2球,净胜球数为(+4)+(–2)=+(4–2)=2 黄队共进2球,失4球,净胜球为(+2)+(–4)=–(4–2)=–2 篮球共进1球,失1球,净胜球数为
(+1)+(–1)=0
海平面的高度为0m. 一艘潜艇从海平面先下潜40m, 再上升15m. 求现在这艘潜艇相对于海平面的位置.(上升为正,下潜为负)
潜水艇下潜40m,记作–40m;上升 15m,记作+15m. 根据题意,得(–40)+(+15)= –(40–15)= –25(m)答:现在这艘潜艇位于海平面下25m处.
1. 计算–3+1的结果是( ) A.–2 B.–4 C.4 D.2
2. 计算:|–2+3|= .
解析:|–2+3|=1.
解析:–3+1= –2.
1. 计算:0 +(–2)=( ) A.–2 B.2 C.0 D.–202. 在1,–1,–2这三个数中,任意两数之和的最大值是( ) A.1 B.0 C.–1 D.3
A. a+c<0 B. b+c<0 C. –b+a<0 D.–a+b+c<0
3.已知有理数a, b, c在数轴上的位置如图所示,则下列结论中错误的是( )
A.1 B.–5 C.–5或–1 D.5或1
4.若│x│= 3,│y│= 2,且x>y,则x+y的值为( )
(1) (–0.6)+(–2.7); (2) 3.7+(–8.4);(3) 3.22+1.78; (4) 7+(–3.3).
答案:(1) –3.3 (3) 5
(2) –4.7
解:中午的气温为–25+11= –14(℃), 夜间的气温为–14+(–13)= –27(℃).
某城市一天早晨的气温是–25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
在某次抗洪抢险中,武警战士的冲锋舟沿东西方向的河流抢救灾民. 早晨从A地出发,晚上到达B地. 规定向东为正方向,出发地A记为0,当天航行记录如下(单位:千米):14, –9, 18, –7, 13, –6, 10, –5. 问B地在A地什么位置? 解:14+(–9)+18+(–7)+13+(–6)+10+(–5)=28(千米). 答:B地在A地正东28千米处.
数学七年级上册4.1 整式习题课件ppt: 这是一份数学七年级上册<a href="/sx/tb_c4050871_t3/?tag_id=26" target="_blank">4.1 整式习题课件ppt</a>,文件包含41整式第1课时pptx、41整式第1课时docx、41整式第1课时习题docx等3份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
人教版七年级上册1.3.1 有理数的加法精品课件ppt: 这是一份人教版七年级上册1.3.1 有理数的加法精品课件ppt,文件包含人教版数学七年级上册131《有理数的加法第1课时》课件pptx、人教版数学七年级上册131《有理数的加法第1课时》教案docx、人教版数学七年级上册131《有理数的加法第1课时》课时练docx等3份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
人教版七年级上册1.3.1 有理数的加法说课课件ppt: 这是一份人教版七年级上册1.3.1 有理数的加法说课课件ppt,共22页。PPT课件主要包含了学习目标,新课导入,我是火炬手,合作探究,想一想,比一比,有理数加法法则一,加数异号,加数的绝对值不相等,有理数加法法则二等内容,欢迎下载使用。













