北师大版七年级数学上册中考新趋势(3)规律探究问题课件

这是一份北师大版七年级数学上册中考新趋势(3)规律探究问题课件，共9页。

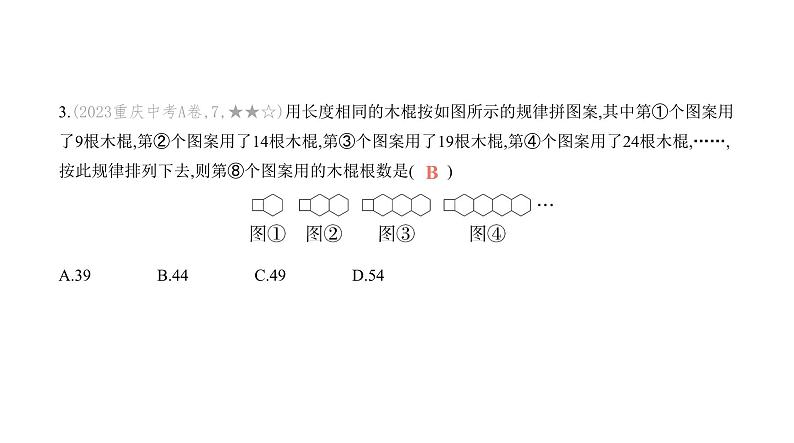
中考新趋势（3）规律探究问题1.(2022新疆中考,9,★☆☆)将全体正偶数排成一个三角形数阵: 按照以上排列的规律,第10行第5个数是 (　　)A.98　　　    B.100　　　    C.102　　　    D.104B由三角形的数阵知,第n行有n个偶数,所以前9行有1+2+3+4+5+6+7+8+9=45个偶数,所以第9行最后一个数为90,所以第10行第5个数是90+2×5=100,故选B.2.(2023黑龙江牡丹江中考,7,★★☆)观察下面两行数:1,5,11,19,29,…;1,3,6,10,15,….取每行数的第7个数,计算这两个数的和是(　　)A.92　　　    B.87　　　    C.83　　　    D.78C观察第2行数可知,第7个数为1+2+3+4+5+6+7=28,观察题中两行数可知第1行的数等于第2行对应位置的数乘2减1,故第1行的第7个数为28×2-1=55,因为28+55=83,所以取每行数的第7个数,这两个数的和是83.故选C.3.(2023重庆中考A卷,7,★★☆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,……,按此规律排列下去,则第⑧个图案用的木棍根数是(　　) A.39　　　    B.44　　　    C.49　　　    D.54B由题图可得,图案①有4+5=9根小木棍,图案②有4+5×2=14根小木棍,图案③有4+5×3=19根小木棍,……所以第 个图案有(4+5n)根小木棍,所以第⑧个图案有4+5×8=44根小木棍.故选B.4.(2023黑龙江绥化中考,21,★★☆)在求1+2+3+…+100的值时,发现:1+100=101,2+99=101,……,从而得到1+2+3+…+100=101×50=5 050.按此方法可解决下面问题.图(1)有1个三角形,记作a1=1;分别连接这个三角形三边中点得到图(2),有5个三角形,记作a2=5;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作a3=9;……,按此方法继续下去,则a1+a2+a3+…+an=　　        .(结果用含n的代数式表示)  (2n-1)n因为题图(1)有1个三角形,记作a1=1;题图(2)有5个三角形,记作a2=5=1+4=1+4×1;题图(3)有9个三角形,记作a3=9=1+4+4=1+4×2;……所以an=1+4(n-1)=4n-3,所以a1+a2+a3+…+an=1+5+9+…+(4n-3)= ·n=(2n-1)n.5.(2023湖北随州中考,15,★★☆)某天老师给同学们出了一道趣味数学题:设有编号为1~100的100盏灯,分别对应着编号为1~100的100个开关,灯分为“亮”和“不亮”两种状态,每按一次开关改变一次相对应编号的灯的状态,所有灯的初始状态为“不亮”.现有100个人,第1个人把所有编号是1的整数倍的开关按一次,第2个人把所有编号是2的整数倍的开关按一次,第3个人把所有编号是3的整数倍的开关按一次,……,第100个人把所有编号是100的整数倍的开关按一次.问最终状态为“亮”的灯共有多少盏?几位同学对该问题展开了讨论:甲:应分析每个开关被按的次数找出规律;乙:1号开关只被第1个人按了1次,2号开关被第1个人和第2个人共按了2次,3号开关被第1个人和第3个人共按了2次,……;丙:只有按了奇数次的开关所对应的灯最终是“亮”的状态.根据以上同学的思维过程,可以得出最终状态为“亮”的灯共有　　　    盏.10因为1号开关被按了1次,2号开关被按了2次,3号开关被按了2次,4号开关被按了3次,5号开关被按了2次,6号开关被按了4次,7号开关被按了2次,8号开关被按了4次,9号开关被按了3次,……,所以n号开关被按的次数等于n的约数的个数.若n的约数个数是奇数,则n一定是平方数.因为100=102,所以100以内(包括100)共有10个平方数,所以最终状态为“亮”的灯共有10盏.