初中数学沪科版九年级上册21.2 二次函数的图象和性质背景图课件ppt

这是一份初中数学沪科版九年级上册21.2 二次函数的图象和性质背景图课件ppt，共32页。

1.(2022黑龙江哈尔滨中考)抛物线y=2(x+9)2-3的顶点坐标是  (　    )A.(9,-3)　　　B.(-9,-3)　　　C.(9,3)　　　D.(-9,3)
解析　由y=2(x+9)2-3可知抛物线的顶点坐标为(-9,-3).
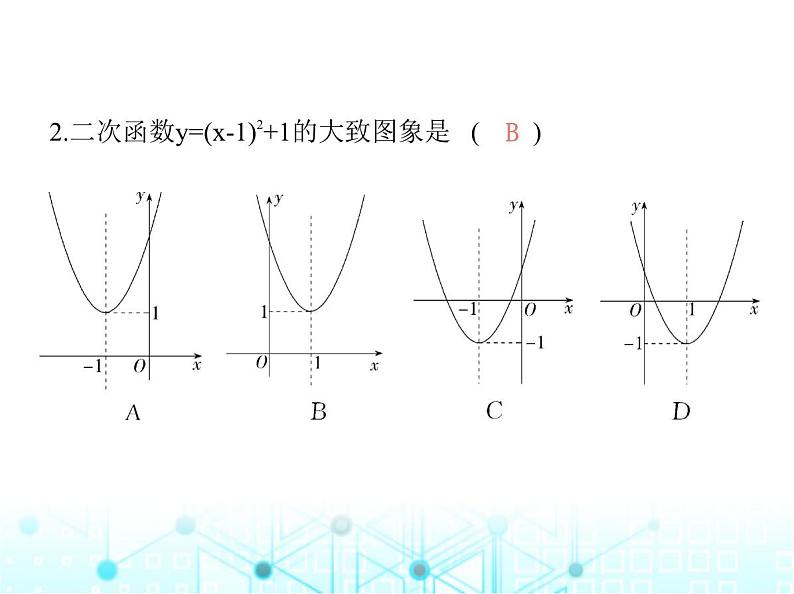
2.二次函数y=(x-1)2+1的大致图象是 (　    ) 　         
解析　在y=(x-1)2+1中,a=1>0,∴抛物线的开口向上,易知顶 点坐标为(1,1),对称轴为直线x=1,故二次函数y=(x-1)2+1的大 致图象是B选项中的图象.
3.(2024安徽合肥滨湖寿春中学期中)已知二次函数y=-2(x-1)2 -3,下列说法正确的是 (　    )A.抛物线的对称轴为直线x=-1B.函数的最大值是3C.抛物线开口向上D.顶点坐标为(1,-3)
解析　∵二次函数y=-2(x-1)2-3的图象的开口向下,对称轴是 直线x=1,∴当x=1时,函数有最大值-3,∴顶点坐标为(1,-3).故 选D.
4.(2024安徽六安皋城中学期中)抛物线y=(x+2)2+3上的点到x 轴最短的距离是　　　    .
解析　∵抛物线y=(x+2)2+3的开口向上,顶点为(-2,3),∴当x= -2时,函数有最小值3,∴抛物线y=(x+2)2+3上的点到x轴最短的距离是3.
5.(易错题)(2024安徽安庆潜山月考)已知抛物线y=-5(x+m)2- 3,当x≥1时,y随x的增大而减小,那么m的取值范围是　　         .
解析　∵抛物线y=-5(x+m)2-3的开口向下,对称轴为直线x=- m,∴在对称轴右侧,y随x的增大而减小.∵当x≥1时,y随x的增 大而减小,∴-m≤1,解得m≥-1.
6.(新独家原创)对于二次函数y=-(x-k)2+k2+1(k为常数),有如 下结论:①该函数图象开口向上;②该函数图象一定经过点(0,1);③该函数图象的顶点在抛物线y=x2+1上;④若函数图象与x轴的一个交点的横坐标为1,则k=1.其中,正确的结论有　    .(填序号)
解析　因为-1<0,所以该函数图象开口向下,故①错误;当x=0时,y=-k2+k2+1=1,所以函数图象经过点(0,1),故②正确;该函数图象的顶点坐标为(k,k2+1),则x=k,y=k2+1,消去k,得y= x2+1,即该函数图象的顶点在抛物线y=x2+1上,故③正确;将x=1,y=0代入y=-(x-k)2+k2+1,得-(1-k)2+k2+1=0,解得k=0,故 ④错误.
7.(新独家原创)(教材变式·P28T12)将抛物线y=a(x+h)2+k先向 下平移2个单位长度,再向左平移3个单位长度,得到抛物线y= -2(x-1)2+3.(M9121002)(1)求a,h,k的值;(2)确定抛物线y=a(x+h)2+k的开口方向,对称轴和顶点坐标;(3)说明二次函数y=a(x+h)2+k的增减性和最值.
解析    (1)将抛物线y=-2(x-1)2+3向上平移2个单位长度,再向 右平移3个单位长度,得抛物线y=-2(x-1-3)2+3+2=-2(x-4)2+5=a (x+h)2+k,∴a=-2,h=-4,k=5.(2)抛物线y=-2(x-4)2+5的开口向下,对称轴是直线x=4,顶点坐 标为(4,5).(3)由抛物线y=-2(x-4)2+5的对称轴是直线x=4,a=-2<0,可知当 x>4时,y随x的增大而减小,当x<4时,y随x的增大而增大.当x= 4时,函数有最大值,最大值为5.
8.(2023广西中考)将抛物线y=x2先向右平移3个单位,再向上 平移4个单位,得到的抛物线是 (　    )A.y=(x-3)2+4　　　B.y=(x+3)2+4C.y=(x-3)2-4　　　D.y=(x+3)2-4
解析　根据平移规律“左加右减,上加下减”,将抛物线y=x2 先向右平移3个单位,再向上平移4个单位,得到的抛物线是y= (x-3)2+4.故选A.
9.(2024安徽合肥包河月考)抛物线y=-2(x-1)2-1可由抛物线y= -2(x+2)2+3平移得到,那么平移的步骤是(M9121002)(　    )A.右移3个单位长度,再下移4个单位长度B.右移3个单位长度,再上移4个单位长度C.左移3个单位长度,再下移4个单位长度D.左移3个单位长度,再上移4个单位长度
解析　抛物线y=-2(x+2)2+3的顶点坐标为(-2,3),抛物线y=-2 (x-1)2-1的顶点坐标为(1,-1),点(-2,3)平移到(1,-1)的方法是右 移3个单位长度,下移4个单位长度,故选A.
10.(2024安徽黄山期中,7,  )若抛物线y=-2(x+m-1)2-3m+6的顶点在第二象限,则m的取值范围是(M9121002)(　    )A.m>1　B.m<2　C.1解析　∵抛物线y=-2(x+m-1)2-3m+6的顶点坐标为(1-m,-3m+ 6),顶点在第二象限,∴1-m<0,-3m+6>0,∴111.(分类讨论思想)(2022浙江衢州中考,10,  )已知二次函数y=a(x-1)2-a(a≠0),当-1≤x≤4时,y的最小值为-4,则a的值为 (M9121002)(　    )A. 或4　　　B. 或- C.- 或4　　　D.- 或4
解析　抛物线y=a(x-1)2-a的对称轴为直线x=1,顶点坐标为(1, -a),当a>0时,在-1≤x≤4中,y有最小值-a,∵y的最小值为-4,∴ -a=-4,∴a=4;当a<0时,在-1≤x≤4中,当x=4时,y有最小值,∴9a -a=-4,解得a=- .综上所述,a的值为4或- ,故选D.
12.(2024安徽阜阳月考,12,  )抛物线y=2(x+1)2+7关于x轴对称的抛物线的表达式为　　　　　　    .
y=-2(x+1)2-7
解析　∵抛物线y=2(x+1)2+7的顶点坐标为(-1,7),∴抛物线y =2(x+1)2+7关于x轴对称的抛物线的顶点坐标为(-1,-7),且开 口向下,∴所求抛物线的表达式为y=-2(x+1)2-7.
13.(2024安徽合肥月考,14,  )如图,二次函数y=a(x+1)2-2的图象过点(1,0).(M9121002) (1)a=　　　　    ;(2)当-2≤x<3时,函数值y的取值范围是　　　　    .
解析    (1)二次函数y=a(x+1)2-2的图象过点(1,0),∴0=a(1+1)2- 2,解得a= .(2)当x=-1时,y=-2,当x=3时,y=6,∴当-2≤x<3时,函数值y的取 值范围是-2≤y<6.
14.(新考向·代数推理)(2024湖北黄石大冶期中,20,  )已知二次函数y=- (x-3m)2+3-3m(m是实数).(M9121002)(1)小明认为当m的值变化时,二次函数图象的顶点始终在一 条直线上运动,你认同他的说法吗?为什么?(2)已知点A(a-5,c),B(6m+4,c)都在该二次函数图象上,求证:c ≤8.
解析    (1)认同,理由如下:抛物线y=- (x-3m)2+3-3m的顶点坐标为(3m,3-3m),∵3m+3-3m=3,∴点(3m,3-3m)在直线y=-x+3上.∴当m的值变化时,二 次函数图象的顶点始终在一条直线上运动.(2)证明:∵A(a-5,c),B(6m+4,c)都在该二次函数图象上,∴A,B 关于直线x=3m对称,∴ =3m,解得a=1,∴A(-4,c).∴c=- (-4-3m)2+3-3m=- m2-9m-1=- (m2+4m+4)+9-1=- (m+
2)2+8,∴关于c与m的二次函数解析式为c=- (m+2)2+8,∴该抛物线的顶点坐标为(-2,8).∵- <0,∴抛物线开口向下,∴c的最大值为8,∴c≤8.
15.(几何直观)已知函数y= 若使y=k成立的x值恰好有2个,则k的值为　 　    .
解析　函数y= 的图象如图,若要使y=k成立的x的值恰好有2个,则直线y=k与该函数图象恰好有2个交点, 根据图象可知当y=-1或y>3时,满足题意,所以k=-1或k>3.
例题　已知二次函数y=(x+1)2-2的图象上有三点A(1,y1),B(2, y2),C(-2,y3),则y1,y2,y3的大小关系为 (　    )A.y1>y2>y3　　　B.y2>y1>y3C.y3>y1>y2　　　D.y3>y2>y1
解析　当x=1时,y1=(1+1)2-2=2;当x=2时,y2=(2+1)2-2=7;当x=-2 时,y3=(-2+1)2-2=-1,∴y2>y1>y3,故选B.
变式1.(二次函数表达式中常数项未知)(2024安徽合肥包河月考) 已知点A(-2,a),B(-1,b),C(3,c)均在抛物线y=-(x-2)2+k上,则a,b, c的大小关系为 (　    )A.a解析　∵抛物线表达式为y=-(x-2)2+k,∴抛物线开口向下,对 称轴为直线x=2,∴距离对称轴越近的点对应的函数值越大. ∵点A(-2,a)到对称轴的距离最远,点C(3,c)最近,∴a2.(点的横坐标未知)已知点A(m,y1)、B(n,y2)(my2　D.无法确定