初中数学沪科版九年级上册第21章 二次函数与反比例函数21.1 二次函数多媒体教学ppt课件

这是一份初中数学沪科版九年级上册第21章 二次函数与反比例函数21.1 二次函数多媒体教学ppt课件，共26页。

1.(2024安徽合肥月考)抛物线y=x2+x+c与y轴的交点坐标为 (0,-3),则抛物线的表达式为 (　    )A.y=x2+x+3　　　B.y=x2+x-3C.y=x2+3x+c　　　D.y=x2-3x+c
解析　∵抛物线y=x2+x+c与y轴的交点坐标为(0,-3),∴c=-3, ∴抛物线的表达式为y=x2+x-3.故选B.
2.(2024安徽六安霍邱期中)已知某抛物线与二次函数y=-5x2 的图象的开口大小相同,开口方向相反,且顶点坐标为(1,2 023),则该抛物线对应的函数表达式为 (　    )A.y=5(x-1)2+2 023B.y=-5(x-1)2+2 023C.y=5(x+1)2+2 023D.y=-5(x+1)2+2 023
解析　∵抛物线的顶点坐标为(1,2 023),∴抛物线的表达式 为y=a(x-1)2+2 023.∵抛物线y=a(x-1)2+2 023与二次函数y=-5 x2的图象的开口大小相同,开口方向相反,∴a=5,∴抛物线的 表达式为y=5(x-1)2+2 023.故选A.
3.(新独家原创)二次函数y=x2+bx+c的图象如图所示,则该函 数的表达式为　　　　    . 
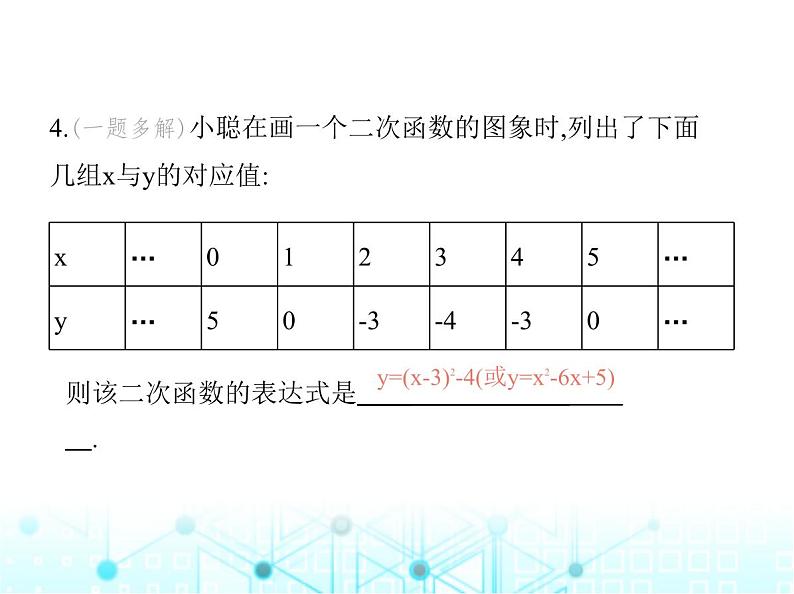
4.(一题多解)小聪在画一个二次函数的图象时,列出了下面 几组x与y的对应值:
则该二次函数的表达式是　　 　　    .
y=(x-3)2-4(或y=x2-6x+5)
解析　解法一:设二次函数的表达式为y=ax2+bx+c,把(0,5),(1, 0),(2,-3)代入,得 解得a=1,b=-6,c=5,所以二次函数的表达式为y=x2-6x+5.解法二:由表格数据,并结合二次函数图象的对称性可得图象 顶点为(3,-4),设二次函数的表达式为y=a(x-3)2-4(a≠0),将(1, 0)代入得4a-4=0,解得a=1,∴该二次函数的表达式为y=(x-3)2- 4(或y=x2-6x+5).
解法三:由表格知函数图象与x轴交于点(1,0),(5,0),所以设二 次函数的表达式为y=a(x-1)(x-5),将(0,5)代入,得a=1,所以该 二次函数的表达式为y=(x-1)(x-5)(或y=x2-6x+5).
方法归纳　确定二次函数表达式的方法已知抛物线上三个点的坐标,则用一般式y=ax2+bx+c;已知抛 物线的顶点,则用顶点式y=a(x+h)2+k;已知抛物线与x轴两交 点的横坐标,则用交点式y=a(x-x1)(x-x2).
5.根据下列条件求函数表达式.(1)已知二次函数y=ax2+bx+c的图象过点(0,2)、(1,3)、(2,2), 求这个二次函数的解析式;(2)已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0, 8),求抛物线的表达式;(3)已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9), 求这个二次函数的表达式.
解析    (1)把(0,2)、(1,3)、(2,2)代入y=ax2+bx+c,得  解得 ∴二次函数的表达式为y=-x2+2x+2.(2)设抛物线的表达式为y=a(x+2)(x-4)(a≠0),把C(0,8)代入得 -8a=8,解得a=-1,∴抛物线的表达式为y=-(x+2)(x-4)=-x2+2x+8.(3)∵顶点坐标为(8,9),
∴设所求二次函数的表达式为y=a(x-8)2+9(a≠0).把(0,1)代入得a(0-8)2+9=1,∴a=- ,∴y=- (x-8)2+9,即y=- x2+2x+1.
6.(和差法求面积)(2024安徽淮南月考)如图,抛物线与x轴交 于A,B两点,其中A点坐标为(-1,0),M(2,9)为抛物线的顶点.(M 9121002)(1)求抛物线的表达式.(2)求四边形OBMC的面积. 
解析    (1)设抛物线的表达式为y=a(x-2)2+9,将A(-1,0)代入,得a=-1.∴y=-(x-2)2+9.(2)如图,连接MC,OM,BM,过点M作MN⊥OB,垂足为N,易得ON=2,OC=5,OB=5,MN=9,∴S四边形OBMC=S△MOC+S△MOB= ×5×2+ ×5×9= . 
解析　∵抛物线y=ax2+bx的顶点坐标为A(3,3),∴ 解得 ∴该抛物线的表达式为y=- x2+2x.故选B.
8.(2024浙江杭州西湖期中,9,  )已知某二次函数图象上有两点A(x1,y1),B(x2,y2),当20;当x1解析　当二次函数图象开口向上时,在对称轴左边,y随x的增 大而减小;在对称轴右边,y随x的增大而增大.当20,x2-x1>0,∴y2>y1.∴当x>2时,y随x的增大而增大.当x10,∴y29.(新考向·开放性试题)(2024上海闵行月考,8,  )已知抛物线y=ax2+bx+c的顶点在直线y=x上,且开口向下,请写出一 个满足上述条件的抛物线的表达式:　　 　　　    .
解析　∵抛物线y=ax2+bx+c开口向下,∴a<0.∵抛物线y=ax2 +bx+c的顶点在直线y=x上,∴- = ,即b2-2b-4ac=0,如:a=-1,b=c=0符合题意,此时y=-x2.答案不唯一.
10.(2024安徽黄山休宁期中,13,  )已知二次函数的图象与x轴的两个交点A,B关于直线x=-1对称,且AB=6,顶点在函 数y=2x的图象上,则这个二次函数的表达式为　　　　　     　    .(M9121002)
解析    ∵对称轴为直线x=-1,且图象与x轴交于A、B两点, AB=6,∴抛物线与x轴交于(-4,0),(2,0),顶点坐标的横坐标为- 1.∵顶点在函数y=2x的图象上,∴y=2×(-1)=-2,∴顶点坐标为 (-1,-2),设二次函数的表达式为y=a(x+1)2-2,把(2,0)代入得,0=9a-2,解得a= ,∴y= (x+1)2-2= x2+ x- .
11.(教材变式·P29T16)(2024安徽淮南洞山中学月考,21,  )如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0).(M9121002)(1)求抛物线的表达式和对称轴.(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.(3)该抛物线上有一点D(x,y),使得 =  ,求点D的坐标(点D与点A不重合).
解析    (1)∵抛物线经过点B(1,0),C(5,0),∴设抛物线的表达式为y=a(x-1)(x-5),把A(0,4)代入得4=5a,∴a= ,∴抛物线表达式为y= (x-1)(x-5)= x2- x+4.抛物线的对称轴为x= =3.(2)存在,如图,连接AC,与对称轴的交点即为点P,连接PA,PB, AB,此时△PAB的周长最小.设直线AC的表达式为y=kx+b,
∵A(0,4),C(5,0),∴ 解得 ∴直线AC的表达式为y=- x+4.把x=3代入,得y= ,∴点P的坐标为 . 
(3)∵抛物线y= x2- x+4的顶点坐标为(3,-3.2),S△ABC=S△DBC,∴D点的纵坐标为4,把y=4代入y= x2- x+4,得 x2- x+4=4,解得x=0或6.∴点D的坐标为(0,4)或(6,4).∵点D与点A不重合,∴D点坐标为(6,4).
12.(几何直观)(新考法)如图,已知平面直角坐标系中的四个 点:A(0,2),B(1,0),C(3,1),D(2,3).二次函数y=ax2+bx+c的图象经 过其中任意三个点,当a的值最大时,二次函数的表达式为     　 　　　    .